ICM實用模型及例題（D題）

國內(nèi)常說的美國大學(xué)生數(shù)學(xué)建模學(xué)術(shù)活動，其實是由兩種類型的學(xué)術(shù)活動組成，MCM即Mathematical Contest in Modeling，直譯為數(shù)學(xué)建模學(xué)術(shù)活動，和ICM即The Interdisciplinary Contest in Modeling，直譯為交叉學(xué)科建模學(xué)術(shù)活動，兩者名稱不同，題目的風(fēng)格有較大的差異。ICM學(xué)術(shù)活動題目更開放，問題更“大”，更宏觀，篇幅較長，往往是全球范圍內(nèi)共同關(guān)心的問題，因此一般不依賴特定的文化背景或生活習(xí)慣，近幾年ICM學(xué)術(shù)活動要求論文正文部分不超過20頁。

D題：operations?research/network science 問題簡介

自2016年開始，ICM由原來的一道題增至三道題，一般為D題、E題、F題，分別為operations research/network science、environmental science和policy這三種類型。首先我們介紹一下D題也就是operations research/network science這個部分。

D題一般是運(yùn)籌學(xué)和網(wǎng)絡(luò)科學(xué)的問題，所用到模型、算法、軟件比較集中，有章可循。運(yùn)籌學(xué)是以整體最優(yōu)為目標(biāo)，從系統(tǒng)的觀點(diǎn)出發(fā)，力圖以整個系統(tǒng)最佳的方式來解決該系統(tǒng)各部門之間的利害沖突的一門學(xué)科。它對所研究的問題求出最優(yōu)解，尋求最佳的行動方案，所以它也可看成是一門優(yōu)化技術(shù)，提供的是解決各類問題的優(yōu)化方法。

而網(wǎng)絡(luò)科學(xué)是近幾年的一個熱門研究領(lǐng)域，比如著名的“哥尼斯堡七橋”問題，其實就是網(wǎng)絡(luò)科學(xué)較早的實際問題，歐拉在1736年用抽象分析法解決了這個問題，這也使歐拉成為圖論〔及拓?fù)鋵W(xué)〕的創(chuàng)始人。如果對求解最優(yōu)解問題和圖論問題感興趣，或者對這些領(lǐng)域的相關(guān)知識和軟件都比較熟悉，選題時可以重點(diǎn)關(guān)注D題。今天我們首先介紹這道題常用的四種數(shù)學(xué)模型，分別是Programming數(shù)學(xué)規(guī)劃、complex network復(fù)雜網(wǎng)絡(luò)、Queuing排隊論和Clustering聚類分析。

Programming 數(shù)學(xué)規(guī)劃

一般地，優(yōu)化模型可以表述如下：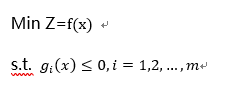

這是一個多元函數(shù)的條件極值問題，其中 x = [ x 1 , x 2 , … , x n ]。許多實際問題歸結(jié)出的這種優(yōu)化模型，但是其決策變量個數(shù) n 和約束條件個數(shù) m 一般較大，并且最優(yōu)解往往在可行域的邊界上取得，這樣就不能簡單地用微分法求解，數(shù)學(xué)規(guī)劃就是解決這類問題的有效方法。三要素：決策變量、目標(biāo)函數(shù)、約束條件適用場景：

1.實際對象特征間及特征與環(huán)境間的交互不存在非線性關(guān)系的優(yōu)化問題

2.需利用非線性刻畫對限制條件或當(dāng)前局勢進(jìn)行描述的優(yōu)化問題

3.決策控制域離散且域中相鄰兩個元素間測度相等的優(yōu)化問題

4.需在多個目標(biāo)間進(jìn)行權(quán)衡達(dá)到整體局勢最優(yōu)的優(yōu)化問題

5.以時間劃分階段的動態(tài)過程的優(yōu)化問題

建模步驟：

Step 1. 尋求決策，即回答什么？必須清楚，無歧義。

Step 2. 確定決策變量

第一來源：Step 1的結(jié)果，用變量固定需要回答的決策

第二來源：由決策導(dǎo)出的變量（具有派生結(jié)構(gòu)）

其它來源：輔助變量（聯(lián)合完成更清楚的回答）

Step 3. 確定優(yōu)化目標(biāo)

用決策變量表示的利潤、成本等。

Step 4. 尋找約束條件

決策變量之間、決策變量與常量之間的聯(lián)系。

第一來源：需求；

第二來源：供給；

其它來源：輔助以及常識。

Step 5. 構(gòu)成數(shù)學(xué)模型

將目標(biāo)以及約束放在一起，寫成數(shù)學(xué)表達(dá)式。常見類型：

線性規(guī)劃 （目標(biāo)函數(shù)及約束條件均為線性函數(shù)）

整數(shù)規(guī)劃 （決策變量部分或全部被限制為整數(shù)）

多目標(biāo)規(guī)劃 （具有多于一個的目標(biāo)函數(shù)）

動態(tài)規(guī)劃（把多階段過程轉(zhuǎn)化為一系列單階段問題，逐個求解）

complex network 復(fù)雜網(wǎng)絡(luò)

在我們的現(xiàn)實生活中，許多復(fù)雜系統(tǒng)都可以建模成一種復(fù)雜網(wǎng)絡(luò)進(jìn)行分析，比如常見的電力網(wǎng)絡(luò)、航空網(wǎng)絡(luò)、交通網(wǎng)絡(luò)、計算機(jī)網(wǎng)絡(luò)以及社交網(wǎng)絡(luò)等等。具有自組織、自相似、吸引子、小世界、無標(biāo)度中部分或全部性質(zhì)的網(wǎng)絡(luò)稱之為復(fù)雜網(wǎng)絡(luò)，言外之意，復(fù)雜網(wǎng)絡(luò)就是指一種呈現(xiàn)高度復(fù)雜性的網(wǎng)絡(luò)。

適用場景l(fā)社團(tuán)檢測：潛在客戶挖掘、關(guān)聯(lián)群體風(fēng)險分析等；l網(wǎng)絡(luò)中心性分析：網(wǎng)頁排名（PageRank），供應(yīng)鏈核心企業(yè)識別，信息傳播樞紐節(jié)點(diǎn)識別等；網(wǎng)絡(luò)傳播預(yù)測：流行病傳播，金融風(fēng)險傳播，輿論傳播；

網(wǎng)絡(luò)關(guān)系滲透：節(jié)點(diǎn)之間的關(guān)系（三度影響）；

關(guān)聯(lián)交易分析及投融資黑洞：虛假交易，擔(dān)保圈分析等。

基本概念

l節(jié)點(diǎn)、邊

l關(guān)聯(lián)與鄰接

l度 k、平均度 <k>

l節(jié)點(diǎn)的度分布p(k)

l最短路徑與平均路徑長度（Dijkstra算法）

常用網(wǎng)絡(luò)

ER模型：Erd?s和Rényi （ER）最早提出隨機(jī)網(wǎng)絡(luò)模型并進(jìn)行了深入研究，他們是用概率統(tǒng)計方法研究隨機(jī)圖統(tǒng)計特性的創(chuàng)始人。給定N個節(jié)點(diǎn)，沒有邊，以概率p用邊連接任意一對節(jié)點(diǎn)，用這樣的方法產(chǎn)生一隨機(jī)網(wǎng)絡(luò)。

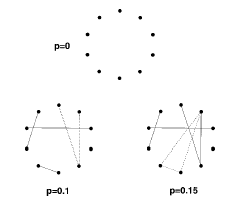
節(jié)點(diǎn)的度分布：平均值為的泊松分布小世界模型: 為了描述從一個局部有序系統(tǒng)到一個隨機(jī)網(wǎng)絡(luò)的轉(zhuǎn)移過程，Watts和 Strogatz（WS）提出了一個新模型，通常稱為小世界網(wǎng)絡(luò)模型。WS模型始于一具有N個節(jié)點(diǎn)的一維網(wǎng)絡(luò)，網(wǎng)絡(luò)的節(jié)點(diǎn)與其最近的鄰接點(diǎn)和次鄰接點(diǎn)相連接，然后每條邊以概率p重新連接。

約束條件為節(jié)點(diǎn)間無重邊，無自環(huán)。當(dāng)p等于0時，對應(yīng)于規(guī)則圖。兩個節(jié)點(diǎn)間的平均距離<L>線性地隨N增長而增長，集聚系數(shù)大。當(dāng)p等于1時，系統(tǒng)變?yōu)殡S機(jī)圖。 <L>對數(shù)地隨N增長而增長，且集聚系數(shù)隨N減少而減少。

在p等于（0，1）區(qū)間任意值時，<L>約等于隨機(jī)圖的值，網(wǎng)絡(luò)具有高度集聚性---小世界效應(yīng)。

無標(biāo)度(Scale-free)網(wǎng)絡(luò): 無標(biāo)度模型由Albert-László Barabási和Réka Albert在1999年首先提出，現(xiàn)實網(wǎng)絡(luò)的無標(biāo)度特性源于眾多網(wǎng)絡(luò)所共有的兩種生成機(jī)制：（ⅰ）網(wǎng)絡(luò)通過增添新節(jié)點(diǎn)而連續(xù)擴(kuò)張； （ⅱ）新節(jié)點(diǎn)擇優(yōu)連接到具有大量連接的節(jié)點(diǎn)上。

具有性質(zhì)：度分布呈冪率分布、中樞節(jié)點(diǎn)出現(xiàn)、魯棒性、脆弱性。

Queuing 排隊論

面對擁擠現(xiàn)象，人們總是希望盡量設(shè)法減少排隊，通常的做法是增加服務(wù)設(shè)施，但是增加的數(shù)量越多，人力、物力的支出就越大，甚至?xí)霈F(xiàn)空閑浪費(fèi)，如果服務(wù)設(shè)施太少，顧客排隊等待的時間就會很長，這樣對顧客會帶來不良影響。顧客排隊時間的長短與服務(wù)設(shè)施規(guī)模的大小，就構(gòu)成了設(shè)計隨機(jī)服務(wù)系統(tǒng)中的一對矛盾。

如何做到既保證一定的服務(wù)質(zhì)量指標(biāo)，又使服務(wù)設(shè)施費(fèi)用經(jīng)濟(jì)合理，恰當(dāng)?shù)亟鉀Q顧客排隊時間與服務(wù)設(shè)施費(fèi)用大小這對矛盾。這就是隨機(jī)服務(wù)系統(tǒng)理論——排隊論所要研究解決的問題。適用場景排隊論里把要求服務(wù)的對象統(tǒng)稱為“顧客”,而把提供服務(wù)的人或機(jī)構(gòu)稱為“服務(wù)臺”或“服務(wù)員”。不同的顧客與服務(wù)組成了各式各樣的服務(wù)系統(tǒng)。顧客為了得到某種服務(wù)而到達(dá)系統(tǒng)、若不能立即獲得服務(wù)而又允許排隊等待，則加入等待隊伍，待獲得服務(wù)后離開系統(tǒng)。

主要流程

l? 確定時間分布（到達(dá)時間和服務(wù)時間）

l? 研究系統(tǒng)理論分布的概率特征

l? 研究系統(tǒng)狀態(tài)的概率

l? 求解概率分布和特征數(shù)

l? 指標(biāo)優(yōu)化與運(yùn)營優(yōu)化

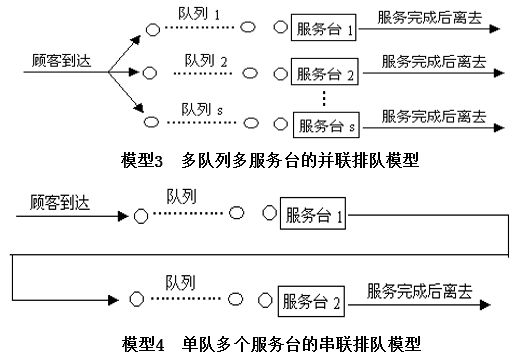
排隊模型

根據(jù)顧客到達(dá)和服務(wù)臺數(shù)，排隊過程可用下列模型表示：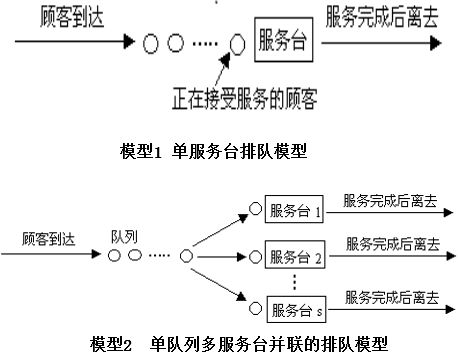

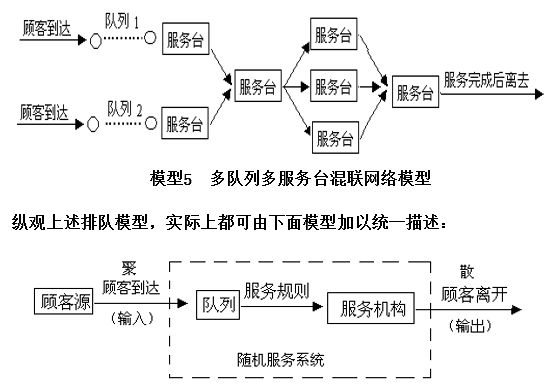
Clustering 聚類分析

聚類分析顧名思義是一種分類的多元統(tǒng)計分析方法。按照個體或樣品的特征將它們分類，使同一類別內(nèi)的個體具有盡可能高的同質(zhì)性，而類別之間則應(yīng)具有盡可能高的異質(zhì)性。

常見類型l劃分

聚類? k-means、k-medoids、k-modes、k-medians、kernel k-mea

層次聚類 Agglomerative 、divisive、BIRCH、ROCK、Chameleo

密度聚類 DBSCAN、OPTICS

網(wǎng)格聚類? STING

模型聚類? GMM

圖聚類? Spectral Clustering（譜聚類）偏最小二乘回歸

主要流程

1.對數(shù)據(jù)進(jìn)行變換處理；（不是必須的，當(dāng)數(shù)量級相差很大或指標(biāo)變量具有不同單位時是必要的）

2.構(gòu)造n個類，每個類只包含一個樣本；

3.計算n個樣本兩兩間的距離；

4.合并距離最近的兩類為一新類；

5.計算新類與當(dāng)前各類的距離，若類的個數(shù)等于1，轉(zhuǎn)到6；否則回4；

6.畫聚類圖；

7.決定類的個數(shù)，從而得出分類結(jié)果。指標(biāo)優(yōu)化與運(yùn)營優(yōu)化
常見距離度量