AMC10/AMC12美國數學競賽知識點題型分析

雖說稱之為學術活動，但其實AMC是一個定時考試，并根據年級分為AMC 8 、AMC 10和AMC 12。這里，小編對2002年~2018年累計34套AMC 10試題進行了分析，一起來看看考題中都涉及了哪些知識點題型吧！

01面積（Area）

在AMC 10中，每套題里面平均差不多有4道和面積相關，而且往往都是連著出，上一道面積，下一道還是面積......為什么會有這么多面積題？小編認為主要原因是美國在上個世紀60年代砍掉了數學教材中的幾何部分，因此幾何面積題成了很多學生的軟肋。另一個原因當然就是為了人工智能技術的基礎——微積分做準備。在AMC 10題目中，很多時候面積會和勾股定理、相似三角形、托勒密定理、海倫公式等摻雜在一起出題，有的題目還需要做適當的輔助線。

題目翻譯如下：

等邊三角形ABC，邊長為2。M是AC邊中點，C為BD邊中點，求三角形CDM的面積。

此題可以直接套用等邊三角形CAB的面積公式：√3/4 *a^2=√3/4*2^2=√3(√表示根號)。因為M為AC的中點，做ME垂直于BC于E,AF垂直于BC于F,因此三角形CME相似于三角形CAF,ME為AF的一半，也就是三角形CDM的高為三角形CAB的一半，而它們的底相同，因此三角形CDM的面積為三角形CAB的一半，即√3/2。故而答案為C。

02日常應用（Apply）

日常應用題在AMC 10的學術活動題中非常具有特色，如2018年AMC 10的第20題：

題目翻譯如下：

一個二維碼由7*7個網格組成，分別由黑色或者白色填充，不能全黑或者全白。二維碼必須是對稱的，即無論它旋轉多少個90度，形狀應該保持一樣。另外該圖形沿對角折疊、水平/垂直中線翻轉應該也是一樣的。那么，這樣的圖案一共有多少種式樣？

本題的解法如下：將7X7的正方形沿著橫軸中心線、縱軸中心線、兩條對角線分別對折四次，最后得到如下三角形：

根據題意，只有圖中三角形里面的10個區域的顏色是可變的，一旦這個三角形里面的10個區域顏色確定，整個7X7區域格子里面的顏色都可以根據對稱性得到。按照乘法原理，10個格子共有2^10=1024個不同的配色方案，去掉兩個全白和全黑:? 1024-2=1022。因此答案選(B)。

03解方程（Equations）

函數方程是微積分和線性代數的基礎，而微積分和線性代數是人工智能技術的基礎。這里我們看一道線性方程的送分題-2002年AMC 10第12題：

題目翻譯如下：

k對應哪個數值的話，使得方程中的x沒有解？

如果學生有平面幾何概念的話，應該會立刻反應過來：x無解的話，就意味兩條線要平行。平行的話，讓 k+2=7 就可以了。于是答案自然選(E)。

04概率計算（Probability）

AMC 10中的概率題可謂五花八門，與各種各樣的知識點結合在一起出題。2011年AMC 10B第16題，就是一道和幾何面積計算相結合的概率題目。

題目翻譯如下：

正八邊形被圖中所示分割，對它扔飛鏢的話，落在中間正方形的概率是多少？

看題意可知，題目主要求的就是面積比的計算，概率就是中間正方形和整個八邊形的面積比就好了，故而答案選(A)。

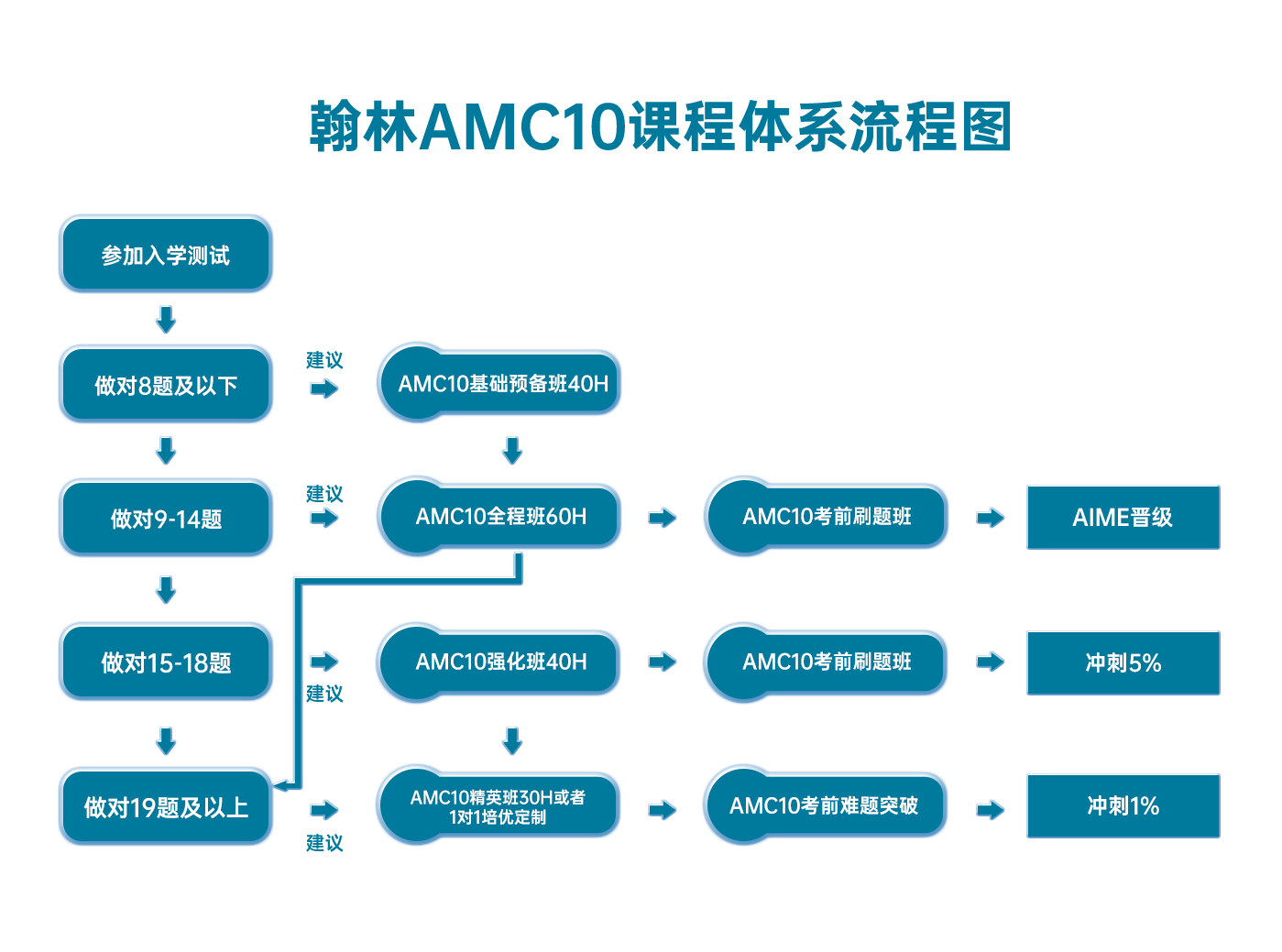
翰林AMC10課程體系流程圖

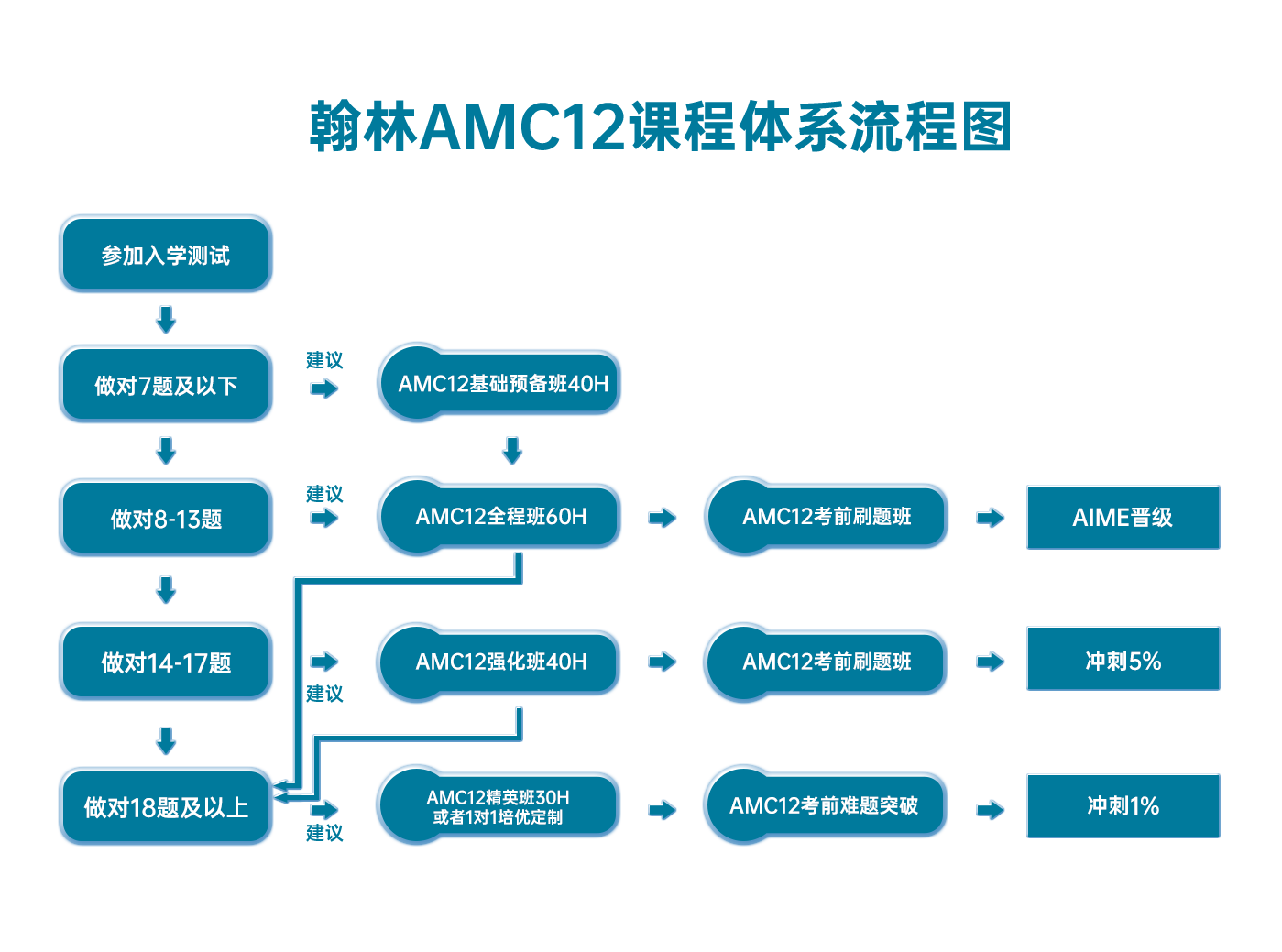
翰林AMC12課程體系流程圖