A-Level數(shù)學(xué)：相關(guān)變化率（Related Rates）解題思路

在ALevel數(shù)學(xué)關(guān)于微分的內(nèi)容中，讓很多學(xué)生都感到頭疼的一類習(xí)題就是關(guān)于相關(guān)變化率（Related Rates）的問題，這一類問題經(jīng)常會出現(xiàn)很多變量，讓學(xué)生不知道該如何下手。今天我們來詳細(xì)分析一下這類習(xí)題，找到快速解題的竅門。?

1我們先看一道例題：

Air is being pumped into a spherical balloon (see Figure 3.38) at a rate of 4.5 cubic feet per minute.Find the rate of change of the radius when the radius is 2 feet.

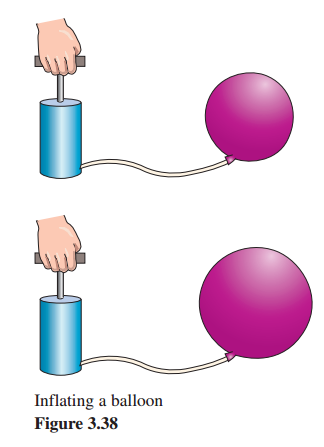
本題的意思是說：每分鐘給氣球打氣的速度是4.5立方英尺每分鐘，求當(dāng)氣球的半徑正好是2英尺時的那一瞬間，氣球半徑增加的速率。

有生活常識的人都知道，如果體積增加的速率是恒定的，那么在氣球比較小的時候，半徑增加的會比較快，而當(dāng)氣球已經(jīng)很大的時候，半徑增加的就會比較緩慢了，所以雖然體積增加的速率恒定，但是半徑增加的速率不是定值。那么該如何找到體積增加速率和半徑增加速率的關(guān)系呢？

本題的關(guān)鍵在于，要找到已知條件和未知量，首先半徑是2英尺，而本題中的每分鐘充氣的體積，實(shí)際上就是體積相對于時間的變化率，也就是dV/dt。本題要求的是半徑增加的速率，其實(shí)也就是半徑相對于時間的變化率：dR/dt。

對于本題，我們需要找到不帶微分符號時，已知變量和未知變量的恒等關(guān)系，也就是體積V和R兩個變量的關(guān)系，然后對時間t做微分，就能得到dR/dt的表達(dá)式。過程如下：

?所以針對related rates一類的問題，不管題目有多復(fù)雜，我們只需要找到兩個相關(guān)變量的恒等關(guān)系，這類關(guān)系可以是面積或體積的恒等式，也可以是勾股定理，三角函數(shù)關(guān)系等不管變量如何變化，等式都保持相等的關(guān)系。最后再對時間t做微分，就能找到未知量的微分值了。

2那么看看下面這道題，你是否有思路了呢？

Find the rate of change in the angle of elevation of the camera shown in Figure 3.40 at 10 seconds after lift-off.

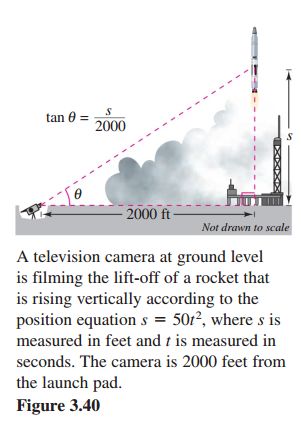
解題過程如下：