2016PUPC普林斯頓大學物理競賽Onsite真題與答案免費下載

歷年PUPC普林斯頓大學物理學術活動真題與答案免費下載

Onsite現場學術活動部分

翰林國際教育全網首發

力爭超快速發布最全資料

為你

千千萬萬遍

2016PUPC普林斯頓大學物理學術活動完整版真題免費下載

Onsite現場學術活動部分此卷共3題

但每題下分不同數量的小題

完整版下載鏈接見文末

真題預覽：

Problem 1. A Jelly-Filled Universe (10 points total)

Suppose the Universe is ?lled with some strange gelatinous substance which produces a pseudo-drag force. A particle of mass m will experience a braking force (which we will also call the pseudo-drag force)

F = - ka

where k is some positive constant and a is the particle’s acceleration. For the following questions, assume the particle moves in one dimension for simplicity.

a) (1 point) Suppose there are no other forces on the particle. Describe the motion of the particle’s position x(t) for all times t≥0, assuming its initial speed v(0) = v0 and initial position x(0) = x0.

b) (1 point) Now suppose the particle experiences a constant external force Fext > 0 beginning at t = 0. Describe the motion of the particle’s position x(t) for all times t≥0, assuming its initial speed v(0) = v0 and initial position x(0) = x0.

c) (1 point) What is the total work W done on the particle during the time interval 0 ≤t≤T under this constant applied force? (Include the work done by the applied force and the pseudo-drag force.)

d) (2 points) Describe the physical implication of the pseudo-drag force F for the particle. In particular, describe how this pseudo-drag force di?ers from kinetic friction (a constant braking force) and low-velocity viscous drag (a braking force proportional to the particle’s speed). Please be as speci?c as possible in your explanation.

e) (1 point) Suppose the particle is dropped near the Earth’s surface where there is a gravitational ?eld strength g. How long does it take (t) for the particle to fall through a height h? (Assume the force of gravity is mg downward, and does not depend appreciably on the height of the particle above the surface of the Earth.)

f) (2 points) It is possible to recover the same result as in part e) for the movement of the particle by removing the pseudo-drag force F and replacing g with an e?ective gravitational ?eld ge?.Find this effective field for a given value of k and m. Consider the limits in which m→0 and m→∞. Do your answers make sense? Explain.

g) (2 points) In electromagnetism, the Abraham-Lorentz force is a braking force that depends on the derivative of the particle’s acceleration:

where q is some constant and m is the particle’s mass, included for convenience. Including a time-varying external force Fext(t), the equation of motion is

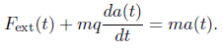
We can integrate this expression to ?nd the solution for a(t),

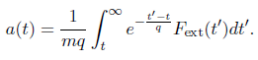
Suppose a constant external force Fext(t)= Fext is turned on at some faraway time t = T> 0 and lasts for all t≥T . What is the acceleration a(t) of the particle for t≥0 according to the solution for a(t) given above? What is strange about this situation? Please be speci?c by commenting on any times of interest.

完整版真題下載鏈接請注冊或登錄后查看

文件為PDF格式

推薦使用電腦下載

 

2016PUPC普林斯頓大學物理學術活動完整版答案免費下載

請點擊訪問下方鏈接進入下載頁面

2016 PUPC Onsite完整版真題答案

 

如需打包下載，請聯系小助手了解更多

免費領取最新年份學術活動真題及解析

翰林學員全站資料免費打包下載，專享高速下載通道。

[vc_btn title="查看更多PUPC相關詳情" color="primary" align="center" i_icon_fontawesome="fa fa-globe" css_animation="zoomIn" button_block="true" add_icon="true" link="url:http%3A%2F%2Fwww.linstitute.net%2Farchives%2F26506||target:%20_blank|"]