2022AP物理C力學北美卷FRQ已放出，附考情分析

各位AP小伙伴們好呀~2022年5月10日進行的AP物理C力學考試已經結束，本場考試為線下紙筆考試，CB官網已更新了2022AP物理C力學北美FRQ真題。

2022年的AP物理C力學考試已經結束，今天官方放出了兩個Set的FRQ，我們趕緊一起來看看都考了哪些內容吧！

試卷整體難度和知識點

兩個Set的對應題目考的知識點相近，第1題主要是考察牛頓運動定律，第2題主要在考察動量和實驗分析，第3題主要是考察轉動的牛頓第二定律。整體的難度中等，有的題目和往年題目極為相似；此外，涉及實驗分析和圖像解釋的題目可能略難，剛體轉動的題目個別小題可能略難。整體相比2021年考試難度來看，難度系數有所下降。

與2021年題目對比的點評

第1道題比較新穎，之前沒有出現過類似的變力分析問題，可以作為今年新出現的題目類型進行重點研究；第2道題目，相信大家都比較眼熟，第2道題目考察的題目模型和2021年很類似，都是一個物塊沿斜面下滑，在右端有運動檢測裝置等，只不過第2道題目引入了動量和能量，并在此基礎上進行考察；第3道題目的圖像問題和2021年極為類似，考察的知識點和解題方法近乎吻合。

因此，大家如果做了2021年的北美題的話，相信大家這套題目一定可以拿到理想的分數。

逐題點評

第一題
Set1
一個電動機在左側下方提供一個大小恒定不變的拉力，放在桌子上的小物體受到繩子拉力的作用往左滑動，小物體和桌面之間有摩擦力，均不考慮其余位置的摩擦力和其余物體的質量。
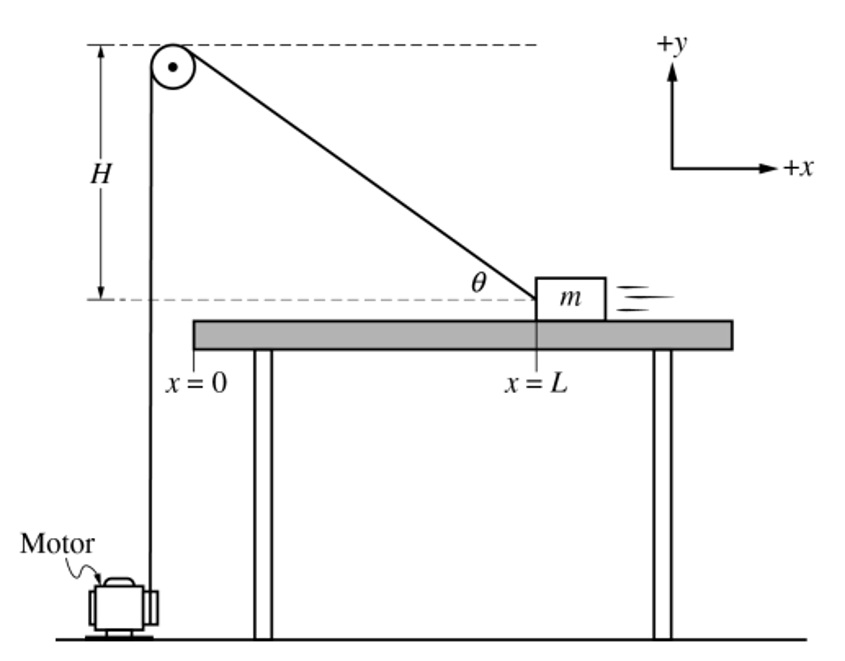（a）畫出小物塊在x=L位置處的受力分析圖。
考點：Unit 2牛頓運動定律中的受力分析圖。
思路：小物塊受到向下的重力、向上的支持力、沿繩子斜向左上方的拉力和水平向右的摩擦力。在這里要特別注意摩擦力的方向，與物塊的運動方向相反。

（b）推導繩子與水平面的夾角θ與水平位置x的函數關系。
考點：Unit 1位移和三角函數關系。
思路：從圖中可以看出，位移x、豎直高度H、滑輪到物塊的斜著的繩子的長度，構成一個直角三角形，利用正切函數關系，可以找到繩子與水平面的夾角θ與水平位置x的表達式。

（c）
i：推導物塊受到的支持力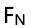和水平位置x的函數關系。
考點：Unit 2中的牛頓第一定律。
思路：根據豎直方向上受力平衡，可以寫出，得出，然后再將sinθ按照三角形的邊之間的關系進行替換就好。

ii：推導物體所受的合力與水平位置x的關系表達式。
考點：Unit 2中的牛頓第二定律。
思路：根據水平方向上物體受力不平衡、豎直方向上物體受力平衡可以推斷出，物體受到的合力就是水平方向上的合力。根據受力分析圖，寫出水平方向的牛頓第二定律表達式：?;再將摩擦力利用進行替換帶入可以得到合力的最終受力表達式，最后的話，再將三角函數表達式利用幾何三角形的邊進行替換就好。

（d）寫出（但不用求解）從x=L到x=0繩子拉力做功的表達式。
考點：Unit 3中的變力做功問題。
思路：根據變力做功，直接寫出變力做功積分式就好。

（e）比較繩子從x=L到x=L/2、從x=L/2到x=0做功的大小。
考點：Unit 3中的變力做功問題。
思路：從x=L到x=L/2、x=L/2到x=0拉力的水平位移都一樣，因此判斷拉力前后兩段位移做功大小，只需要判斷拉力的水平分力大小就好，拉力的水平分量表達式為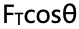，隨著物塊向左滑動，θ在增大，cosθ在減小，所以拉力的水平分力也在減小，所以平均來看，前半段拉力的水平分力大于后半段的水平分力，所以前半段拉力做功會更大一些。

掃碼添加翰林顧問老師，可一對一制定國際課程規劃
【免費領取】AP備考資料合集~

?Set2
一個質量為m的小雪橇在受到繩子的拉力和桌面摩擦力的條件下，給定一個初速度，向右進行滑動。其中繩子的拉力大小恒定不變，不考慮其余位置的摩擦和其余物體的質量。
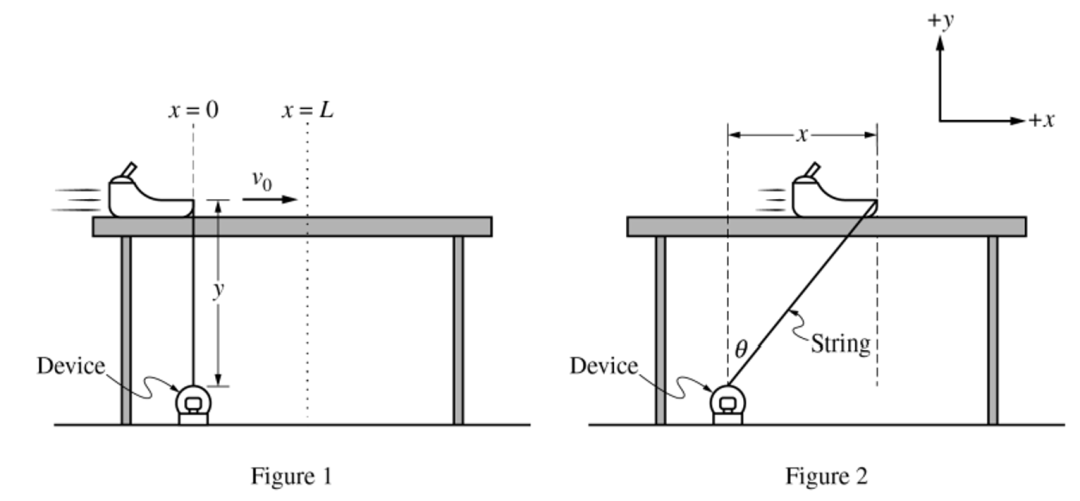（a）畫出運動開始很小一段時間后（小雪橇停止運動前的某個時刻），小雪橇的受力分析圖。
考點：Unit 2牛頓運動定律中的受力分析圖。
思路：小雪橇受到向下的重力、向上的支持力、沿繩子斜向左下方的拉力和水平向左的摩擦力。在這里要特別注意摩擦力的方向，與小雪橇的運動方向相反。

（b）推導繩子與豎直方向的夾角θ與運動距離x的函數關系。
考點：Unit 1位移和三角函數關系。
思路：從圖中可以看出，位移x、豎直高度y、左下方設備到小雪橇的斜著的繩子的長度，構成一個直角三角形，利用正切函數關系，可以找到繩子與豎直方向的夾角θ與運動距離x的表達式。

（c）
i：推導物塊受到的支持力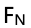和水平位置x的函數關系。
考點：Unit 2中的牛頓第一定律。
思路：根據豎直方向上受力平衡，可以寫出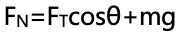，然后再將cosθ按照三角形的邊之間的關系進行替換就好。

ii：推導物體所受的合力與水平位置x的關系表達式。
考點：Unit 2中的牛頓第二定律。
思路：根據水平方向上物體受力不平衡、豎直方向上物體受力平衡可以推斷出，物體受到的合力就是水平方向上的合力，根據受力分析圖，寫出水平方向的牛頓第二定律表達式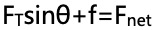：;再將摩擦力利用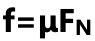進行替換帶入可以得到合力的最終受力表達式，最后的話，再將三角函數表達式利用幾何三角形的邊進行替換就好。

（d）推導從x=0到x=L，繩子拉力做功的表達式。
考點：Unit 3中的變力做功問題。
思路：根據變力做功，寫出變力做功積分表達式，再進行數學積分就好。這個題物理方程不難，但是數學積分難度會相應大一些，大家計算要仔細認真。

（e）小雪橇在運動水平距離2L后靜止。比較系統從x=0到x=L、從x=L到x=2L由于摩擦力做功損耗掉的能量的大小。
考點：Unit 3中的非保守力做功和能量守恒。
思路：摩擦力做功的數值的絕對值就是系統損耗的能量。從x=0到x=L、從x=L到x=2L摩擦力的位移都一樣，因此只需要比較這兩段過程中摩擦力的大小，結合摩擦力的表達式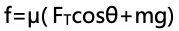，, θ在增大，cosθ在減小，摩擦力在減小，因此平均來看，前半段的摩擦力要比后半段的摩擦力要大，所以前半段摩擦力做功的絕對數值要大。

第二題
?Set1
小車1從斜面上往下滑，撞到靜止在水平面上的小車2，然后二者共速在一起朝右運動。水平面的最右方有一個運動探測器，可以用來記錄小車的運動。整個過程中不考慮摩擦和轉動影響。
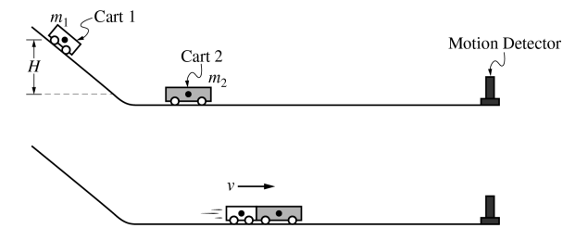（a）在碰撞過程中，比較小車1給小車2和小車2給小車1的沖量的大小關系。
考點：Unit 4中的沖量、Unit 2中的牛頓第三定律。
思路：根據牛頓第三定律，小車1給小車2的力和小車2給小車1的力等大反向，再結合二者作用力的時間相同，可以得出二者的沖量是相等的。

（b）畫出碰撞前后，小車1和小車2的動量隨時間變化的圖像。
考點：Unit 4中的動量、動量定理和動量守恒定律。
思路：兩小車碰撞前，小車1由靜止開始下滑，速度均勻增加，到達平面后速度不變，因此小車1的動量先是直線型增加，再保持不變，小車2動量為0保持不變；碰撞后，因為系統動量守恒，小車2獲得動量后保持不變，小車1的動量會減小一部分，然后繼續保持不變；在這里要特別注意，小車1的動量減少量和小車2的動量增加量大小一樣，建議在圖像中把這層含義表示出來。

（c）題干給出了小車碰撞后的速度表達式，要我們進行證明。
考點：Unit 4中的動量守恒定律和Unit 3中的機械能守恒。
思路：利用機械能守恒，可以求得小車1運動到水平面（和小車2碰撞前）的速度；再根據動量守恒定律，可以求得系統碰撞后的速度表達式，即可得證。

（d）對于不同的釋放高度H，測出系統共速后的速度v，給出了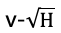的圖像。要求畫出最優擬合線并計算小車2的質量。
考點：最優擬合線的畫法和通過直線斜率計算目標變量。
思路：根據上一問的速度表達式，最優擬合線應該是一條直線，注意畫的時候不是連接所有點畫折線而是要讓不在直線上的數據大致平均分布在直線兩側，比如五個數據點可能有兩個在直線上、一個在直線上方、兩個在直線下方。這條直線的斜率是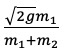，計算斜率的時候要注意不是取數據點而是取直線上的點，得到斜率之后通過計算便可得出小車2的質量。

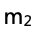（e）通過比較實驗測得的數據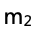和實際用天平測得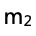的大小，來推斷小車1質量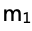與0.25 kg的大小關系。
考點：實驗誤差分析。
思路：可以根據斜率表達式，推導和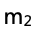的關系，從而再根據題干已知條件，再去反推小車1的質量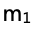和0.25 kg的大小關系。

?Set2
物塊1在壓縮彈簧一段距離的情況下，被彈簧推開（物塊1與彈簧不連接）獲得一個初速度，與水平面上靜止的物塊2發生完全非彈性碰撞，碰撞后一起共速向右運動。水平面右側有運動探測器，用來記錄系統的運動。不考慮各種摩擦。
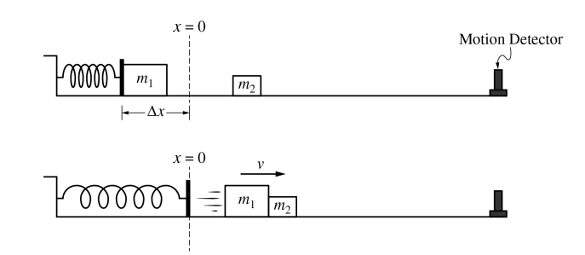（a）在碰撞過程中，比較物塊1給物塊2和物塊2給物塊1的沖量的大小關系。
考點：Unit 4中的沖量、Unit 2中的牛頓第三定律。
思路：根據牛頓第三定律，物塊1給物塊2的力和物塊2給物塊1的力等大反向，再結合二者作用力的時間相同，可以得出二者的沖量是相等的。

（b）畫出碰撞前后，物塊1和物塊2的動量隨時間變化的圖像。
考點：Unit 4中的動量、動量定理和動量守恒定律。
思路：兩小車碰撞前：物塊1先是受到彈簧的彈力做變速運動（隨著彈簧伸長，加速度越來越小），離開彈簧后，做勻速運動，因此物塊1的動量先是曲線增加（上凸類型）再保持不變，物塊2動量為0保持不變；
碰撞后：因為系統動量守恒，物塊2獲得動量后保持不變，物塊1原來的動量減小一部分，然后繼續保持不變；在這里要特別注意，物塊1的動量減少量和物塊2的動量增加量大小一樣，建議在圖像中把這層含義表示出來。

（c）題干給出了物塊碰撞后的速度表達式，要我們進行證明。
考點：Unit 4中的動量守恒定律和Unit 3中的機械能守恒。
思路：利用機械能守恒，可以求得物塊1運動到水平面（和物塊2碰撞前）的速度；再根據動量守恒定律，可以求得系統碰撞后的速度表達式，即可得證。

（d）對于不同的彈簧壓縮距離Δx，測出系統共速后的速度v，給出了v-Δx的圖像。要求畫出最優擬合線并計算物塊2的質量。
考點：最優擬合線的畫法和通過直線斜率計算目標變量。
思路：根據上一問的速度表達式，最優擬合線應該是一條直線，注意畫的時候不是連接所有點畫折線而是要讓不在直線上的數據大致平均分布在直線兩側，比如五個數據點可能有兩個在直線上、一個在直線上方、兩個在直線下方。這條直線的斜率是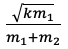，計算斜率的時候要注意不是取數據點而是取直線上的點，得到斜率之后通過計算便可得出物塊2的質量。

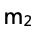（e）通過比較實驗測得的數據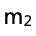和實際用天平測得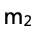的大小，來推斷彈簧勁度系數k與150 N/m的大小關系。
考點：實驗誤差分析。
思路：可以根據斜率表達式，推導彈簧勁度系數k和物塊2的質量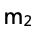的關系，從而再根據題干已知條件，再去反推彈簧勁度系數k與150 N/m的大小關系。

第三題
?Set1
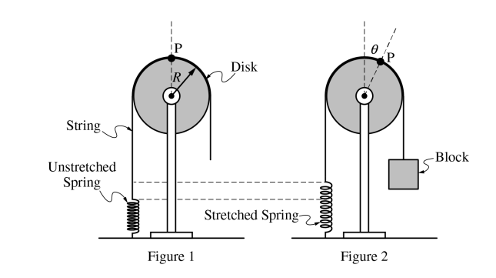
一個有支柱的固體圓盤可以繞圓盤中心做無摩擦轉動。一條繩子通過圓盤并且在圓盤的最頂端被固定住，記該點為P點。繩子的左下端連著一個彈簧，右端連著一個物塊。開始彈簧處于原長，在此初始條件下，開始慢慢釋放右端的物塊，使其緩慢運動，最終達到平衡的狀態，此時圓盤的最頂端轉過的角度為θ。題干中給出了圓盤圍繞其中心旋轉的轉動慣量表達式。
（a）推導物塊的質量表達式。
考點：Unit 2中的牛頓第一定律和胡克定律。
思路：物塊受到繩子的拉力和自身重力，并且處于受力平衡；繩子的拉力又等于彈簧的拉力，因此，彈簧的拉力大小就是物塊的重力大小；彈簧的拉力可以通過胡克定律F=kx求解，彈簧的形變量在這道題為圓盤轉過的弧長，即θR。再利用彈簧的彈力除以g，即可求得物塊的質量大小。

（b）在題干初始平衡的條件下，突然把連接物塊的繩子剪斷。畫出剪斷繩子的瞬間，圓盤的受力分析圖。
考點：Unit 5中的受力分析圖。
思路：剪斷繩子的瞬間，圓盤受到質心發出向下的重力，質心方向向上的支持力和圓盤左端繩子和圓盤分離處沿切線方向向下的拉力。

（c）推導繩子剪斷瞬間的系統角加速度的表達式。
考點：Unit 5中力矩的計算，轉動形式的牛頓第二定律。
思路：圓盤受到三個力，但只有拉力是有力矩的，剪斷繩子瞬間，拉力的大小為kθR，拉力的力臂為R，拉力的力矩為，再結合轉動形式的牛頓第二定律，τ=Iα，可以得出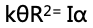，再代入圓盤的轉動慣量，從而可以得出圓盤的角加速度。

（d）畫出繩子剪斷后，圓盤的角速度隨時間變化的圖像。時間截止到P點重新回到最高點的時刻。
考點：Unit 5中力矩的計算，轉動形式的牛頓第二定律，角速率和角加速度的關系。
思路：根據（c）問，可以判斷圓盤在P點重新回到最高點的過程中一直處于加速轉動的狀態，因此角速度在不斷增大；而且，根據（c）中推出的角速度的表達式，可以看出角加速度隨著θ的減小也會減小；因此，在轉動過程中，θ在減小，所以角加速度也在減小，所以角速度-時間圖像的斜率（斜率是角加速度）也在不斷減小，因此，角速度-時間圖像是上凸函數類型，且在P點重新回到最高點時，角速度達到最大，角加速度為0。

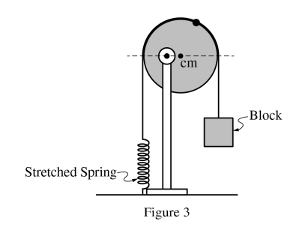
（e）轉軸的支點位置改變后，圓盤受到的力的力矩和（b）問相比，是否發生變化，是變大還是變小。
考點：Unit 5中力矩的計算。
思路：支點改變后，圓盤受到的重力開始出現力矩，而（b）問沒有，因此，重力力矩變大；拉力的力臂更加靠近轉軸中心，力臂減小，所以拉力的力矩比（b）問中下降，因此，拉力力矩變小。支柱給的支持力依舊沒有力矩，故保持不變。

Set2
一根均勻的質量為m長度為L的棒子，左端連著一根彈簧，距左端L/4的位置有一個支點。開始由于一個學生右端拖著棒子，彈簧處于原長狀態；然后，同學的手緩慢放松，棒子右端緩慢下降，最終在棒子水平的時候，同學的手徹底撤去，系統此時也處于平衡狀態。題干給出木棒圍繞該質點的轉動慣量為I。
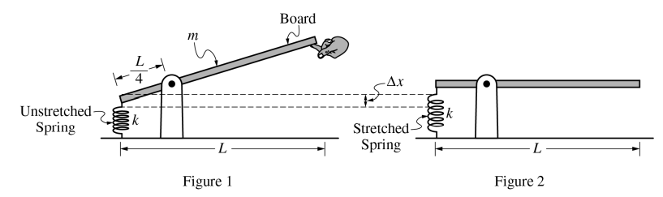（a）畫出棒子水平位置平衡狀態下的受力分析圖。
考點：Unit 5中的受力分析圖。
思路：棒子在最左端受到向下的彈簧的拉力，距離棒子左端L/4處，受到向上支點給的支持力；距離棒子左端L/2處，受到豎直向下的自身的重力。在轉動的受力分析圖里，物體受到的力不可以進行平移，要引起注意。

（b）推導木棒處于水平位置平衡狀態時，彈簧的伸長量Δx的表達式。
考點：Unit 5中力矩的計算、轉動形式的牛頓第一定律和胡克定律。
思路：木棒受到三個力，以支點為轉動中心，只有彈簧的彈力和木棒自身的重力有力矩，且這兩個力的力矩方向相反，大小相等。根據轉動形式的牛頓第一定律，可以列出
kΔxL/4=mgL/4,從而可以計算得出Δx的表達式。
（c）另外一個學生在右端施加了一個新的力將木棒壓至如下圖所示位置，此時彈簧的伸長量為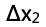，然后學生由靜止釋放木棒。（手施加的力突然撤掉）
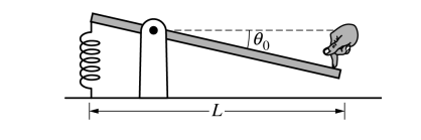i：畫出木棒由靜止開始轉動至水平位置的過程中，角加速度隨時間變化的表達式。
考點：Unit 5中力矩的計算，轉動形式的牛頓第二定律，角加速度。
思路：木棒由靜止釋放后，木棒受到的彈簧的力矩大于自身重力的力矩，所以木棒受到的合力矩為τ= (kΔx-mg)Lcosθ/4，Δx為彈簧的伸長量, θ為木棒與水平位置的夾角；根據轉動形式的牛頓第二定律，τ=Iα，可以得出， (kΔx-mg)Lcosθ/4= Iα；

隨著時間的延伸，木棒受到的合力矩在減小，角加速度也在變小，但是角速度卻在增加，因此位移變化的越來越快，力矩變化的速率也會變快，所以角加速度和時間圖像的斜率會越來越陡；木棒處于水平位置時，木棒受到的合力矩為0，因此角加速度為0，所以角加速度是一個隨著時間不斷減小，并且在木棒回到水平位置的時刻減小到0的一個上凸函數類型。

ii：推導初始釋放位置處，角加速度的表達式。
考點：Unit 5中力矩的計算，轉動形式的牛頓第二定律，角加速度。
思路：木棒由靜止釋放后，木棒受到的彈簧的力矩大于自身重力的力矩，所以木棒受到的合力矩為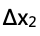，為彈簧的伸長量,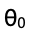為木棒與水平位置的夾角；根據轉動形式的牛頓第二定律，τ=Iα，可以得出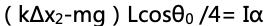，；經過進一步化簡，便可得出角加速度的表達式。

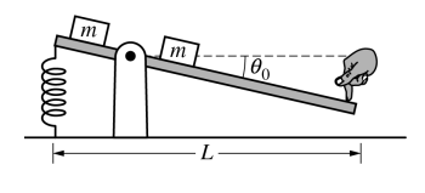
（d）如下圖所示，在距離支點相同的位置處，固定兩個質量為m的小物塊，并在此前提下，木棒又被推至相同的位置處，并進行釋放。問此時的角加速度和沒有小物塊時的角加速度的大小關系。
考點：Unit 5中力矩的計算，轉動形式的牛頓第二定律，角加速度、轉動慣量。
思路：小物塊添加后，系統的轉動慣量會變大，但是系統的合外力矩卻沒有發生變化；因此，根據轉動形式的牛頓第二定律，可以得出角加速度會下降。

寫在最后
以上就是北美考情的分析了，對于備考明年考試的同學來說，應當注意對基礎公式和模型的掌握，AP的出題風格并不會有太激進或太靈活的變化，和課內的呼應比較好，因此備考前重點研究往年考過的真題或者模考題也非常具有價值。