2022 AP微積分最后沖刺，滿滿大考干貨！

提到AP微積分，可以說是最受中國考生歡迎的科目了，也是AP理科中的5分率王者之一。很多學微積分的同學一開始就是沖著5分去的，然而，考試本身還是有一定難度的，畢竟一年只有這么一次考試機會！

今年的微積分考試時間在5月9日 8 a.m.，時間緊迫，大家要抓緊身邊所有可用資源充分備考！

說到AP考試，MCQ和FRQ里肯定是FRQ最讓大家頭疼——題干又臭又長、要求又多又繁瑣，考試范圍靈活，難題、怪題、偏題層出不窮。而且，這么難的FRQ，在考試中的分值比重還很高！可以稱得上是5分路上的絆腳石了。

不過大家不要被困難絆倒，這里給大家準備了兩道微積分FQR題，快來檢測一下你對FRQ題型的熟悉程度以及對知識點的掌握度～

解析：

我們先來看題目給的條件:

1) 0至4的閉區間f有定義

2) f的一次導

(a)問的是在哪個區間f是增長的，我們知道[f increasing→f'>0][f decreasing→f'<0]。所以現在用圖形計算器畫出f'的圖像，大概找出在0至4的閉區間的范圍內，f'=0和f'>0的分界點。

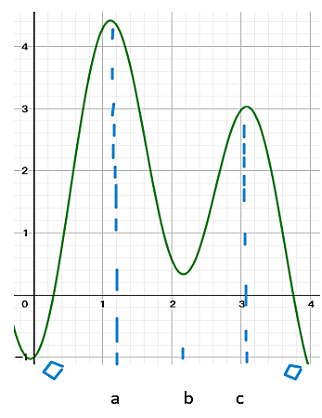
通過畫圖（如上圖）我們得出，在大概0.282和3.758的區域內，f'>0。用到圖形計算器的求解功能，我們可以較準確地算出前面的區間在保留三位小數后是(0.283，3.760)。答案就是：On the open interval between 0.283 and 3.760, f is increasing.

(b)問x是什么值時，f有局部極大值。

注意與globalmaximum 區分：一個函數可有多個local max/min，但是只可有一個global max/min。

看回剛剛用圖形計算器畫的圖，我們知道，在(0,0.283)區間，f值減小；在(0.283，3.760)區間，f值增大；在(3.760,4)區間，f值減小。看著f'圖在三個區間所包圍的面積來看，在(0.283，3.760)區間包圍的正面積最大，所以在當x=3.760時，f有最大值。答案就是：f has a local maxima when x=3.760

(c)問的是，在圖上有幾個拐點。

Inflection point就是函數改變concavity的時候：例如從concave up(f''>0)變成concave down(f''<0)。這道題只問了數量，并沒有問確切的位置，所以步驟相對簡便。

可以看出，在f'的x=a,x=b, 和x=c前后的地方，f''發生了變化。0到a這一段f''>0；a到b這一段f''<0；b到c這一段f''>0；c到4這一段f''<0.因為f''發生了三次變化，所以一共有三個inflection point。答案就是：f has 3 inflection points.

（誤區：不小心把f'的圖當成了f的圖像，直接找concave up/down的圖

希望通過以上的練習，大家能對微積分FRQ的題目設置和易錯點有了更清晰的認識。

掃碼添加翰林顧問老師，可一對一制定國際課程規劃

【免費領取】AP 備考資料合集~