USACO比賽2021年1月銅組考試真題解析+考試入口！

隨著近幾年來出國留學的人越來越多,申本的難度也隨之不斷提高,學生們要有突出的基礎成績,還要有過硬的“軟實力”,才能被名校所青睞。而受全球疫情的影響,準留學生們提升軟實力的機會有所減少,海外項目不能參加,國內部分活動不能順利開展。

那么現階段有什么學術活動活動,既提升學生的綜合能力又能被名校認可,而且國內學生足不出國就能參加。所以小編今天必須來給大家介紹一下：USACO全稱USA Computing Olympiad，美國信息學奧林匹克學術活動。

比賽時間：3 月 25 日-3 月 28 日

比賽入口：usaco.org

報名時間：無需提前報名，賽時登錄賬號即可答題

比賽形式：線上

報名費：無

獲取備賽計劃，考前查缺補漏、重點沖刺

【免費領取】相關真題及解析，還有不定期的高能講座等你來參加！

以下是USACO比賽2021年1月銅組考試真題：第3題，一起來感受下難度吧~

題目解析

N最大為20，直接枚舉的復雜度為O(N*N!)，測試點1-5可以采用直接枚舉，當N比較大時顯然會超時。

采用排列組合和乘法原理可以以較小的復雜度解此題。

以樣例為例：奶牛的高度可以從高到低排序：4 3 2 1，高度為4的奶牛可以安排到2個高度為4的牛棚，因而有2種可能性。高度為3的奶牛可以安排到2個高度為4的牛棚和1個高度為3的牛棚，因而有3種可能性，但由于可以安排高度為4的奶牛的牛棚一定可以安放高度為3的奶牛，這3種可能性中必定有1個用于安放高度為4的奶牛，則最終可能性為3-1=2。同理，高度為2的奶牛可以安排到4個牛棚中，但其中一個用于安放高度為4的奶牛，一個用于安放高度為3的奶牛，則最終可能性為4-1-1=2。高度為1的奶牛也可以安排到4個牛棚中，但一個用于安放高度4，一個用于安放高度3，一個用于安放高度2，則最終可能性為4-1-1-1=1。最后根據乘法原理，安排4頭奶牛的方法數為：2*(3-1)*(4-2)*(4-3)=8。該方法的時間復雜度為O(N^2)。

解法代碼

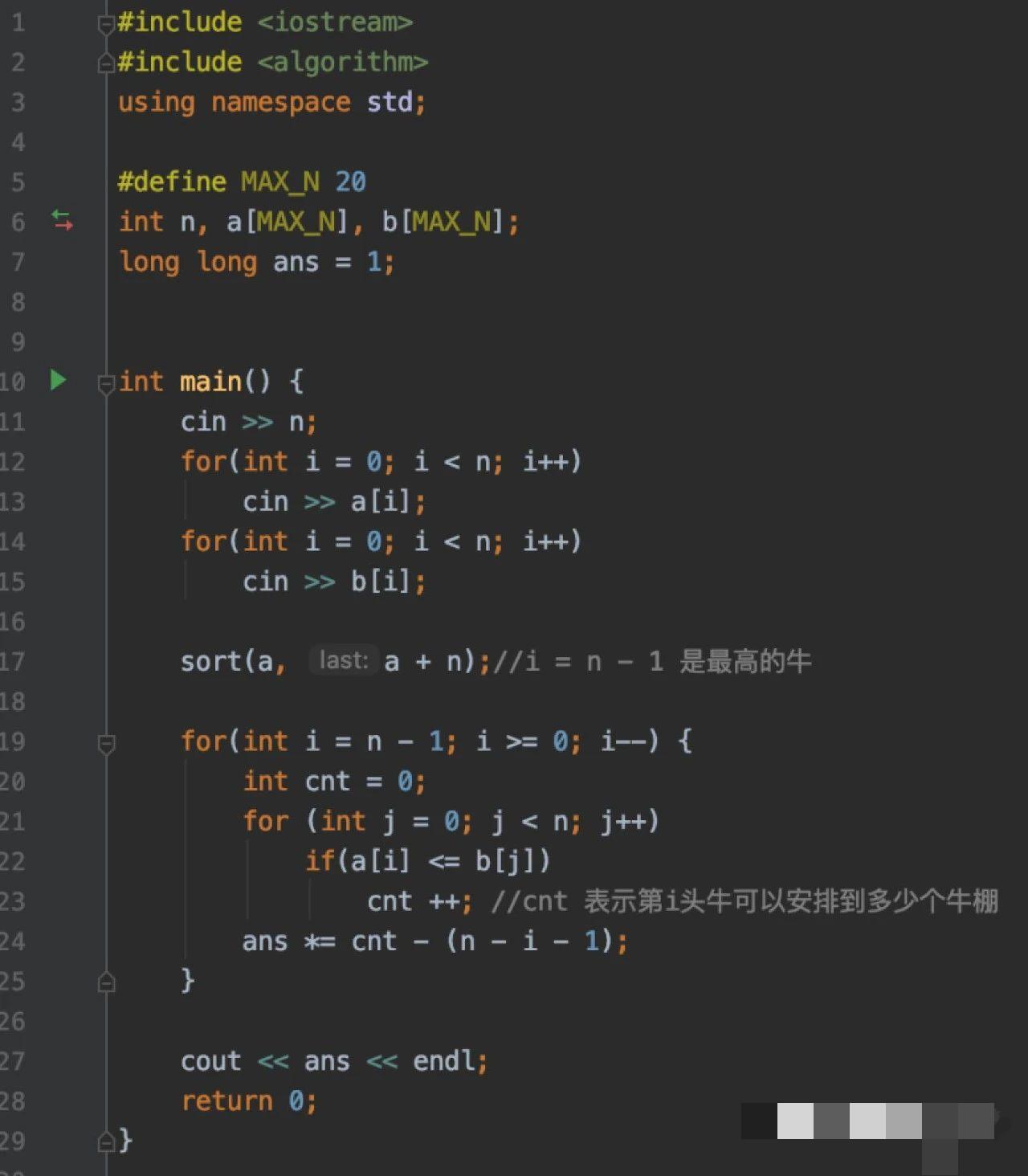
如果改進，時間復雜度還可以優化到O(N*logN)，只是本題的N很小，區別不大。代碼如下，可以思考下原因。

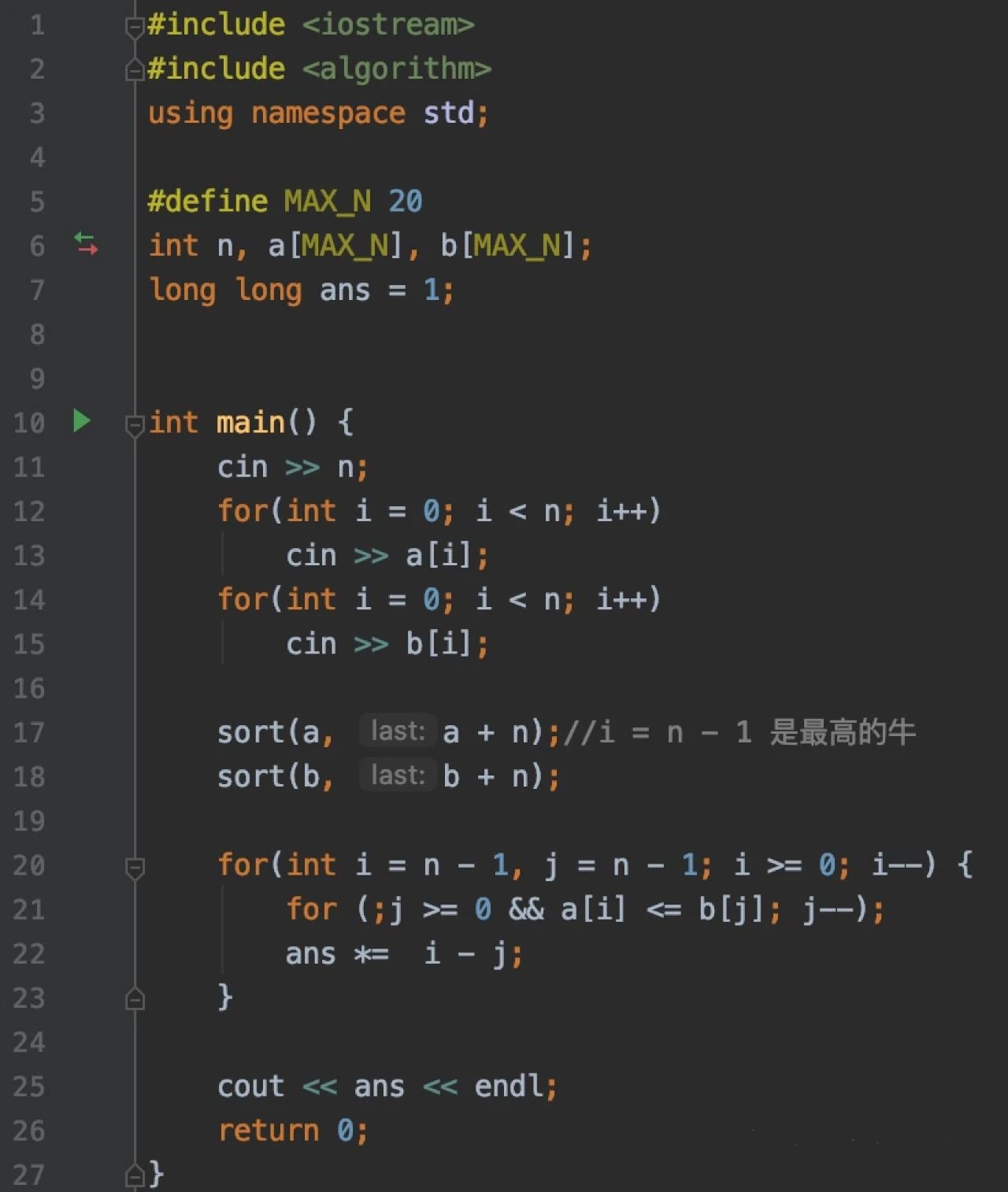
USACO學術活動成本低，收益大，見效快！是一個非常值得參與的學術活動哦~