- 翰林提供學(xué)術(shù)活動(dòng)、國際課程、科研項(xiàng)目一站式留學(xué)背景提升服務(wù)!
- 400 888 0080
1986AIME 真題及答案解析
1986AIME 真題及答案解析
Problem 1
What is the sum of the solutions to the equation?![]() ?
?
Problem 2
Evaluate the product?![]() .
.
Problem 3
If?![]() ?and?
?and?![]() , what is?
, what is?![]() ?
?
Problem 4
Determine?![]() ?if?
?if?![]() ,?
,?![]() ,?
,?![]() ,?
,?![]() , and?
, and?![]() ?satisfy the system of equations below.
?satisfy the system of equations below.
Problem 5
What is that largest?positive integer?![]() ?for which?
?for which?![]() ?is?divisible?by?
?is?divisible?by?![]() ?
?
Problem 6
The pages of a book are numbered?![]() ?through?
?through?![]() . When the page numbers of the book were added, one of the page numbers was mistakenly added twice, resulting in an incorrect sum of?
. When the page numbers of the book were added, one of the page numbers was mistakenly added twice, resulting in an incorrect sum of?![]() . What was the number of the page that was added twice?
. What was the number of the page that was added twice?
Problem 7
The increasing sequence?![]() ?consists of all those positive integers which are powers of 3 or sums of distinct powers of 3. Find the?
?consists of all those positive integers which are powers of 3 or sums of distinct powers of 3. Find the?![]() ?term of this sequence.
?term of this sequence.
Problem 8
Let?![]() ?be the sum of the base?
?be the sum of the base?![]() ?logarithms of all the proper divisors of?
?logarithms of all the proper divisors of?![]() . What is the integer nearest to?
. What is the integer nearest to?![]() ?
?
Problem 9
In?![]() ,?
,?![]() ,?
,?![]() , and?
, and?![]() . An interior point?
. An interior point?![]() ?is then drawn, and segments are drawn through?
?is then drawn, and segments are drawn through?![]() ?parallel to the sides of the triangle. If these three segments are of an equal length?
?parallel to the sides of the triangle. If these three segments are of an equal length?![]() , find?
, find?![]() .
.
Problem 10
In a parlor game, the magician asks one of the participants to think of a three digit number?![]() ?where?
?where?![]() ,?
,?![]() , and?
, and?![]() ?represent digits in base?
?represent digits in base?![]() ?in the order indicated. The magician then asks this person to form the numbers?
?in the order indicated. The magician then asks this person to form the numbers?![]() ,?
,?![]() ,?
,?![]() ,?
,?![]() , and?
, and?![]() , to add these five numbers, and to reveal their sum,?
, to add these five numbers, and to reveal their sum,?![]() . If told the value of?
. If told the value of?![]() , the magician can identify the original number,?
, the magician can identify the original number,?![]() . Play the role of the magician and determine the?
. Play the role of the magician and determine the?![]() ?if?
?if?![]() .
.
Problem 11
The polynomial?![]() ?may be written in the form?
?may be written in the form?![]() , where?
, where?![]() ?and the?
?and the?![]() 's are constants. Find the value of?
's are constants. Find the value of?![]() .
.
Problem 12
Let the sum of a set of numbers be the sum of its elements. Let?![]() ?be a set of positive integers, none greater than 15. Suppose no two disjoint subsets of?
?be a set of positive integers, none greater than 15. Suppose no two disjoint subsets of?![]() ?have the same sum. What is the largest sum a set?
?have the same sum. What is the largest sum a set?![]() ?with these properties can have?
?with these properties can have?
Problem 13
In a sequence of coin tosses, one can keep a record of instances in which a tail is immediately followed by a head, a head is immediately followed by a head, and etc. We denote these by TH, HH, and etc. For example, in the sequence TTTHHTHTTTHHTTH of 15 coin tosses we observe that there are two HH, three HT, four TH, and five TT subsequences. How many different sequences of 15 coin tosses will contain exactly two HH, three HT, four TH, and five TT subsequences?
Problem 14
The shortest distances between an interior diagonal of a rectangular parallelepiped,?![]() , and the edges it does not meet are?
, and the edges it does not meet are?![]() ,?
,?![]() , and?
, and?![]() . Determine the volume of?
. Determine the volume of?![]() .
.
Problem 15
Let triangle?![]() ?be a right triangle in the?
?be a right triangle in the?![]() -plane with a right angle at?
-plane with a right angle at?![]() . Given that the length of the hypotenuse?
. Given that the length of the hypotenuse?![]() ?is?
?is?![]() , and that the medians through?
, and that the medians through?![]() ?and?
?and?![]() ?lie along the lines?
?lie along the lines?![]() ?and?
?and?![]() ?respectively, find the area of triangle?
?respectively, find the area of triangle?![]() .
.
1986AIME 詳細(xì)解析
- Let?
![$y = sqrt[4]{x}$](https://latex.artofproblemsolving.com/f/5/8/f5838ae6bb955f1f7afe1c28d870b6cd091b78ac.png) . Then we have?
. Then we have? , or, by simplifying,
, or, by simplifying,![[y^2 - 7y + 12 = (y - 3)(y - 4) = 0.]](https://latex.artofproblemsolving.com/f/2/1/f2177dfb0ca3080c826bfa7e508ae0dcd37ef80e.png) This means that?
This means that?![$sqrt[4]{x} = y = 3$](https://latex.artofproblemsolving.com/7/2/3/723fc9924d37616a4675a26e831751451b6904d6.png) ?or?
?or? .Thus the sum of the possible solutions for?
.Thus the sum of the possible solutions for? ?is?
?is? .
. - Simplify by repeated application of the?difference of squares.



 ?
?
- Since?
 ?is the reciprocal function of?
?is the reciprocal function of? :
: Thus,?
Thus,? Using the tangent addition formula:
Using the tangent addition formula: .
. - Adding all five?equations?gives us?
 ?so?
?so? . Subtracting this from the fourth given equation gives?
. Subtracting this from the fourth given equation gives? ?and subtracting it from the fifth given equation gives?
?and subtracting it from the fifth given equation gives? , so our answer is?
, so our answer is? .
. - If?
 ,?
,? . Using the?Euclidean algorithm, we have?
. Using the?Euclidean algorithm, we have? ?
? ?
? , so?
, so? ?must divide?
?must divide? . The greatest?integer?
. The greatest?integer? ?for which?
?for which? ?divides?
?divides? ?is?
?is? ; we can double-check manually and we find that indeed?
; we can double-check manually and we find that indeed? .In a similar manner, we can apply synthetic division. We are looking for?
.In a similar manner, we can apply synthetic division. We are looking for? . Again,?
. Again,? ?must be a factor of?
?must be a factor of? .The key to this problem is to realize that?
.The key to this problem is to realize that? ?for all?
?for all? . Since we are asked to find the maximum possible?
. Since we are asked to find the maximum possible? ?such that?
?such that? , we have:?
, we have:? . This is because of the property that states that if?
. This is because of the property that states that if? ?and?
?and? , then?
, then? . Since, the largest factor of 900 is itself we have:?
. Since, the largest factor of 900 is itself we have:?
- Denote the page number as?
 , with?
, with? . The sum formula shows that?
. The sum formula shows that? . Since?
. Since? ?cannot be very large, disregard it for now and solve?
?cannot be very large, disregard it for now and solve? . The positive root for?
. The positive root for? . Quickly testing, we find that?
. Quickly testing, we find that? ?is too large, but if we plug in?
?is too large, but if we plug in? ?we find that our answer is?
?we find that our answer is? .
. - Rewrite all of the terms in base 3. Since the numbers are sums of?distinct?powers of 3, in base 3 each number is a sequence of 1s and 0s (if there is a 2, then it is no longer the sum of distinct powers of 3). Therefore, we can recast this into base 2 (binary) in order to determine the 100th number.?
 ?is equal to?
?is equal to? , so in binary form we get?
, so in binary form we get? . However, we must change it back to base 10 for the answer, which is?
. However, we must change it back to base 10 for the answer, which is? .Notice that the first term of the sequence is?
.Notice that the first term of the sequence is? , the second is?
, the second is? , the fourth is?
, the fourth is? , and so on. Thus the?
, and so on. Thus the? ?term of the sequence is?
?term of the sequence is? . Now out of?
. Now out of? ?terms which are of the form?
?terms which are of the form? ?+?
?+? ,?
,? ?of them include?
?of them include? ?and?
?and? ?do not. The smallest term that includes?
?do not. The smallest term that includes? , i.e.?
, i.e.? , is greater than the largest term which does not, or?
, is greater than the largest term which does not, or? . So the?
. So the? th term will be?
th term will be? , then?
, then? , then?
, then? , then?
, then? , and finally?
, and finally? After the?
After the? th power of 3 in the sequence, the number of terms after that power but before the?
th power of 3 in the sequence, the number of terms after that power but before the? th power of 3 is equal to the number of terms before the?
th power of 3 is equal to the number of terms before the? th power, because those terms after the?
th power, because those terms after the? th power are just the?
th power are just the? th power plus all the distinct combinations of powers of 3 before it, which is just all the terms before it. Adding the powers of?
th power plus all the distinct combinations of powers of 3 before it, which is just all the terms before it. Adding the powers of? ?and the terms that come after them, we see that the?
?and the terms that come after them, we see that the? th term is after?
th term is after? , which is the?
, which is the? th term. Also, note that the?
th term. Also, note that the? th term after the?
th term after the? th power of 3 is equal to the power plus the?
th power of 3 is equal to the power plus the? th term in the entire sequence. Thus, the?
th term in the entire sequence. Thus, the? th term is?
th term is? ?plus the?
?plus the? th term. Using the same logic, the?
th term. Using the same logic, the? th term is?
th term is? ?plus the?
?plus the? th term,?
th term,? . We now have?
. We now have?
- The?prime factorization?of?
 , so there are?
, so there are? ?divisors, of which?
?divisors, of which? ?are proper. The sum of multiple logarithms of the same base is equal to the logarithm of the products of the numbers.Writing out the first few terms, we see that the answer is equal to
?are proper. The sum of multiple logarithms of the same base is equal to the logarithm of the products of the numbers.Writing out the first few terms, we see that the answer is equal to![[log 1 + log 2 + log 4 + ldots + log 1000000 = log (2^05^0)(2^15^0)(2^25^0)cdots (2^65^6).]](https://latex.artofproblemsolving.com/8/5/4/854ec44c63903fd31f1c66109b580c04366c9661.png) Each power of?
Each power of? ?appears?
?appears? ?times; and the same goes for?
?times; and the same goes for? . So the overall power of?
. So the overall power of? ?and?
?and? ?is?
?is? . However, since the question asks for proper divisors, we exclude?
. However, since the question asks for proper divisors, we exclude? , so each power is actually?
, so each power is actually? ?times. The answer is thus?
?times. The answer is thus? .Since the prime factorization of?
.Since the prime factorization of? ?is?
?is? , the number of factors in?
, the number of factors in? ?is?
?is? . You can pair them up into groups of two so each group multiplies to?
. You can pair them up into groups of two so each group multiplies to? . Note that?
. Note that? . Thus, the sum of the logs of the divisors is half the number of divisors of?
. Thus, the sum of the logs of the divisors is half the number of divisors of? ?(since they are asking only for proper divisors), and the answer is?
?(since they are asking only for proper divisors), and the answer is? .
. ![[asy] size(200); pathpen = black; pointpen = black +linewidth(0.6); pen s = fontsize(10); pair C=(0,0),A=(510,0),B=IP(circle(C,450),circle(A,425)); /* construct remaining points */ pair Da=IP(Circle(A,289),A--B),E=IP(Circle(C,324),B--C),Ea=IP(Circle(B,270),B--C); pair D=IP(Ea--(Ea+A-C),A--B),F=IP(Da--(Da+C-B),A--C),Fa=IP(E--(E+A-B),A--C); D(MP("A",A,s)--MP("B",B,N,s)--MP("C",C,s)--cycle); dot(MP("D",D,NE,s));dot(MP("E",E,NW,s));dot(MP("F",F,s));dot(MP("D'",Da,NE,s));dot(MP("E'",Ea,NW,s));dot(MP("F'",Fa,s)); D(D--Ea);D(Da--F);D(Fa--E); MP("450",(B+C)/2,NW);MP("425",(A+B)/2,NE);MP("510",(A+C)/2); /*P copied from above solution*/ pair P = IP(D--Ea,E--Fa); dot(MP("P",P,N)); [/asy]](https://latex.artofproblemsolving.com/8/e/1/8e19916c4ed37209e832673ba0274846bb4c4246.png)
 ?as shown above. As a result of the lines being parallel, all three smaller triangles and the larger triangle are?similar?(
?as shown above. As a result of the lines being parallel, all three smaller triangles and the larger triangle are?similar?( ). The remaining three sections are?parallelograms.By similar triangles,?
). The remaining three sections are?parallelograms.By similar triangles,? ?and?
?and? . Since?
. Since? , we have?
, we have? , so?
, so? .
.- Let?
 ?be the number?
?be the number? . Observe that?
. Observe that? ?so
?so![[mequiv -3194equiv -86equiv 136pmod{222}]](https://latex.artofproblemsolving.com/9/7/2/97290b737bbe1f40c3f47cef903ca8eacfa1f153.png) This reduces?
This reduces? ?to one of?
?to one of? . But also?
. But also? ?so?
?so? . Of the four options, only?
. Of the four options, only? ?satisfies this inequality.
?satisfies this inequality. - Using the?geometric series?formula,?
 . Since?
. Since? , this becomes?
, this becomes? . We want?
. We want? , which is the coefficient of the?
, which is the coefficient of the? ?term in?
?term in? ?(because the?
?(because the? ?in the denominator reduces the degrees in the numerator by?
?in the denominator reduces the degrees in the numerator by? ). By the?Binomial Theorem, this is?
). By the?Binomial Theorem, this is? .Again, notice?
.Again, notice? . So
. So We want the coefficient of the?
We want the coefficient of the? ?term of each power of each binomial, which by the binomial theorem is?
?term of each power of each binomial, which by the binomial theorem is? . The?Hockey Stick Identity?tells us that this quantity is equal to?
. The?Hockey Stick Identity?tells us that this quantity is equal to? .
. - By using the greedy algorithm, we obtain?
 , with?
, with? . We must now prove that no such set has sum greater than 61. Suppose such a set?
. We must now prove that no such set has sum greater than 61. Suppose such a set? ?existed. Then?
?existed. Then? ?must have more than 4 elements, otherwise its sum would be at most?
?must have more than 4 elements, otherwise its sum would be at most? .
. ?can't have more than 5 elements. To see why, note that at least?
?can't have more than 5 elements. To see why, note that at least? ?of its subsets have at most four elements (the number of subsets with no elements plus the number of subsets with one element and so on), and each of them have sum at most 54. By the Pigeonhole Principle, two of these subsets would have the same sum.Thus,?
?of its subsets have at most four elements (the number of subsets with no elements plus the number of subsets with one element and so on), and each of them have sum at most 54. By the Pigeonhole Principle, two of these subsets would have the same sum.Thus,? ?would have to have 5 elements.?
?would have to have 5 elements.? ?contains both 15 and 14 (otherwise its sum is at most?
?contains both 15 and 14 (otherwise its sum is at most? ). It follows that?
). It follows that? ?cannot contain both?
?cannot contain both? ?and?
?and? ?for any?
?for any? , or the subsets?
, or the subsets? ?and?
?and? ?would have the same sum. So now?
?would have the same sum. So now? ?must contain 13 (otherwise its sum is at most?
?must contain 13 (otherwise its sum is at most? ), and?
), and? ?cannot contain 12, or the subsets?
?cannot contain 12, or the subsets? ?and?
?and? ?would have the same sum.Now the only way?
?would have the same sum.Now the only way? ?could have sum at least?
?could have sum at least? ?would be if?
?would be if? . But the subsets?
. But the subsets? ?and?
?and? ?have the same sum, so this set does not work. Therefore no?
?have the same sum, so this set does not work. Therefore no? ?with sum greater than 61 is possible and 61 is indeed the maximum.
?with sum greater than 61 is possible and 61 is indeed the maximum. - Let's consider each of the sequences of two coin tosses as an?operation?instead; this operation takes a string and adds the next coin toss on (eg,?THHTH?+?HT?=?THHTHT). We examine what happens to the last coin toss. Adding?HH?or?TT?is simply an?identity?for the last coin toss, so we will ignore them for now. However, adding?HT?or?TH?switches the last coin.?H?switches to?T?three times, but?T?switches to?H?four times; hence it follows that our string will have a structure of?THTHTHTH.Now we have to count all of the different ways we can add the identities back in. There are 5?TT?subsequences, which means that we have to add 5?T?into the strings, as long as the new?Ts are adjacent to existing?Ts. There are already 4?Ts in the sequence, and since order doesn’t matter between different tail flips this just becomes the ball-and-urn argument. We want to add 5 balls into 4 urns, which is the same as 3 dividers; hence this gives?
 ?combinations. We do the same with 2?Hs to get?
?combinations. We do the same with 2?Hs to get? ?combinations; thus there are?
?combinations; thus there are? ?possible sequences.SLIGHT VARIATION ON FINAL ARGUMENTThe structure of the final order is?T_H_T_H_T_H_T_H_, and there are 4 spots to put the 2 heads in, and 4 spots to put the 5 tails in. By using the formula for distributing r identical objects into n distinct boxes?
?possible sequences.SLIGHT VARIATION ON FINAL ARGUMENTThe structure of the final order is?T_H_T_H_T_H_T_H_, and there are 4 spots to put the 2 heads in, and 4 spots to put the 5 tails in. By using the formula for distributing r identical objects into n distinct boxes? ?and multiplication, the answer is?
?and multiplication, the answer is? ?*?
?*? ?=560
?=560 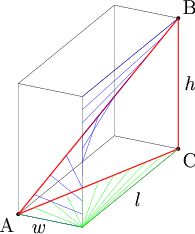
 . All the blue lines are perpendicular lines to?
. All the blue lines are perpendicular lines to? ?and their other points are on?
?and their other points are on? , the main diagonal. The green lines are projections of the blue lines onto the bottom face; all of the green lines originate in the corner and reach out to?
, the main diagonal. The green lines are projections of the blue lines onto the bottom face; all of the green lines originate in the corner and reach out to? , and have the same lengths as their corresponding blue lines. So we want to find the shortest distance between?
, and have the same lengths as their corresponding blue lines. So we want to find the shortest distance between? ?and that corner, which is?
?and that corner, which is? .So we have:
.So we have:![[frac {lw}{sqrt {l^2 + w^2}} = frac {10}{sqrt {5}}]](https://latex.artofproblemsolving.com/0/b/e/0bebea7d48fd0a5003ac28d8f9ca77d4e9440192.png)
![[frac {hw}{sqrt {h^2 + w^2}} = frac {30}{sqrt {13}}]](https://latex.artofproblemsolving.com/2/7/b/27bfdb3306a3193e87d8eecc8b6325a312d3b778.png)
![[frac {hl}{sqrt {h^2 + l^2}} = frac {15}{sqrt {10}}]](https://latex.artofproblemsolving.com/a/c/5/ac5a6c874fcfdd4b9d890e61e3893c6900954eba.png) Notice the familiar roots:?
Notice the familiar roots:? ,?
,? ,?
,? , which are?
, which are? ,?
,? ,?
,? , respectively. (This would give us the guess that the sides are of the ratio 1:2:3, but let's provide the complete solution.)
, respectively. (This would give us the guess that the sides are of the ratio 1:2:3, but let's provide the complete solution.)![[frac {l^2w^2}{l^2 + w^2} = frac {1}{frac {1}{l^2} + frac {1}{w^2}} = 20]](https://latex.artofproblemsolving.com/3/e/9/3e9936cd4e1fcda5d6227228ea37f82bc132500a.png)
![[frac {h^2w^2}{h^2 + w^2} = frac {1}{frac {1}{h^2} + frac {1}{w^2}} = frac {900}{13}]](https://latex.artofproblemsolving.com/9/0/8/908a897173a9680da4f715f78e3264c7d28cc179.png)
![[frac {h^2l^2}{h^2 + l^2} = frac {1}{frac {1}{h^2} + frac {1}{l^2}} = frac {45}{2}]](https://latex.artofproblemsolving.com/9/a/e/9aef0d812e00178d2eaf470ffcc955c630ea9730.png) We invert the above equations to get a system of linear equations in?
We invert the above equations to get a system of linear equations in? ,?
,? , and?
, and? :
:![[frac {1}{l^2} + frac {1}{w^2} = frac {45}{900}]](https://latex.artofproblemsolving.com/0/5/f/05f902c1b2ad93ed0fa5bcacb3b18ca1c87adddb.png)
![[frac {1}{h^2} + frac {1}{w^2} = frac {13}{900}]](https://latex.artofproblemsolving.com/0/b/1/0b1ea7acfaa5f3ffa877563a5b960322779d8e49.png)
![[frac {1}{h^2} + frac {1}{l^2} = frac {40}{900}]](https://latex.artofproblemsolving.com/d/9/3/d9348c7885416f54202794f370267f1d50d01eb9.png)
We see that?
 ,?
,? ,?
,? . Therefore?
. Therefore? .
.- Translate so the?medians?are?
 , and?
, and? , then model the?points?
, then model the?points? ?and?
?and? .?
.? ?is the?centroid, and is the average of the vertices, so?
?is the?centroid, and is the average of the vertices, so?
 ?so
?so


 ?and?
?and? ?are?perpendicular, so the product of their?slopes?is?
?are?perpendicular, so the product of their?slopes?is? , giving
, giving

Combining?
 ?and?
?and? , we get?
, we get?
Using the?determinant?product for area of a triangle (this simplifies nicely, add columns 1 and 2, add rows 2 and 3), the area is?
 , so we get the answer to be?
, so we get the answer to be? .
.
學(xué)術(shù)活動(dòng)報(bào)名掃碼了解!免費(fèi)領(lǐng)取歷年真題!

最新發(fā)布
? 2025. All Rights Reserved. 滬ICP備2023009024號(hào)-1









