丘成桐中學(xué)數(shù)學(xué)獎(jiǎng)中的魔方問題

2018年丘成桐中學(xué)科學(xué)數(shù)學(xué)金獎(jiǎng)?wù)撐氖恰叭赫摵臀迥Х健保髡哂萌赫撝R(shí)解出了五魔方的群結(jié)構(gòu)，給出了求解五魔方的算法。

五魔方（megaminx）是一個(gè)正十二面體，每個(gè)面是一個(gè)正五邊形，原始狀態(tài)下每個(gè)面各有一個(gè)顏色，一共有12個(gè)不同的顏色（還有一種五魔方有6個(gè)不同的顏色）。五魔方玩法和三階魔方一樣，通過旋轉(zhuǎn)各面恢復(fù)原始狀態(tài)，只是難度更大。

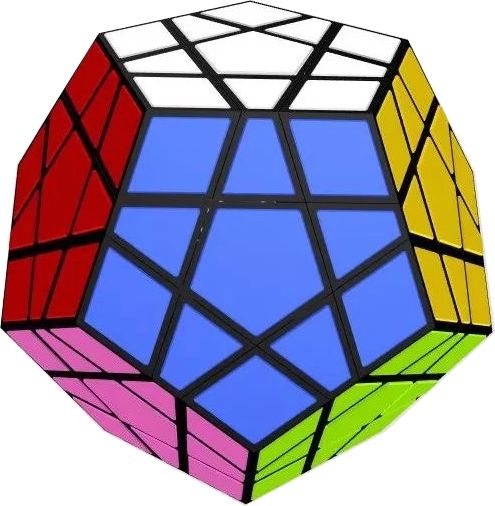
圖片來自獲獎(jiǎng)?wù)哒撐腫1]

五魔方的群結(jié)構(gòu)與三階魔方有所不同，不過研究方法相同，如果掌握了三階魔方群的研究方法，不難導(dǎo)出五魔方的群結(jié)構(gòu)，因此適合中學(xué)生研究。

三階魔方（以下簡(jiǎn)稱魔方）是一款世界流行的玩具，由26個(gè)可見的小立方塊組成一個(gè)立方體，原始狀態(tài)下立方體六個(gè)面各有一個(gè)顏色，通常是紅、橙、藍(lán)、綠、黃和白（見下圖）。旋轉(zhuǎn)魔方的任意一個(gè)面或中間層，會(huì)改變魔方的顏色分布，經(jīng)過一系列隨機(jī)旋轉(zhuǎn)后原始狀態(tài)被打亂，玩家需要旋轉(zhuǎn)魔方恢復(fù)原始狀態(tài)。

圖片來自紐約現(xiàn)代藝術(shù)博物館https://www.moma.org/collection/works/2908?artist_id=5069&locale=zh&page=1&sov_referrer=artis

匈牙利建筑學(xué)教授厄爾諾·魯比克（Erno? Rubik）在1974年發(fā)明了魔方，起初只是為了尋找一種由很多可動(dòng)部件組成且任意活動(dòng)都不會(huì)散架的結(jié)構(gòu)，后來他發(fā)現(xiàn)魔方可以當(dāng)玩具玩，于是在1975年申請(qǐng)了專利。1980年初在Ideal Toy公司的推廣下成為風(fēng)靡全球的玩具，并且有了新名字叫魯比克立方體（Rubik's Cube）。

1981年Douglas Hofstadter在《科學(xué)美國(guó)人》雜志上撰文詳細(xì)介紹了魔方，促進(jìn)了魔方的流行，他本人用了7個(gè)月累計(jì)花費(fèi)50個(gè)小時(shí)復(fù)原了魔方。從1980年到1983年全球賣出了約2億個(gè)魔方，是魔方歷史上最瘋狂的時(shí)刻。?

為什么魔方令大眾著迷？一個(gè)原因是魔方能夠產(chǎn)生數(shù)量巨大的不同狀態(tài)，大約有4.3×1019個(gè)。這么多狀態(tài)如果一秒鐘數(shù)100萬個(gè)也要140萬年才能數(shù)完，因此每個(gè)人拿到的魔方狀態(tài)可能都不一樣，看似簡(jiǎn)單然變化無窮，容易上手卻琢磨不透。

圖片來自文獻(xiàn)[4]

魔方也吸引了數(shù)學(xué)家的注意，John Conway 很早就有了一個(gè)魔方，David Singmaster 在1978年8月的國(guó)際數(shù)學(xué)家大會(huì)上見到了魔方，迫不及待地用一本書換來一個(gè)，然后花了兩周時(shí)間找到了復(fù)原魔方的通用方法。Singmaster在復(fù)原中設(shè)計(jì)了一套標(biāo)記，并且運(yùn)用了數(shù)學(xué)中的群論，他總結(jié)成書，在1980和1981年多次出版[2]。根據(jù)Singmaster的算法，只需要幾分鐘就可以復(fù)原魔方。

Singmaster的書在1981年賣出了5到6萬本，不過跟另一本書比起來就是小巫見大巫了。James?G.?Nourse是斯坦福大學(xué)化學(xué)系員工，在1980年圣誕節(jié)前買了一個(gè)魔方，本打算作為圣誕節(jié)禮物送人，沒想到自己竟然在節(jié)日期間復(fù)原了魔方，于是寫了本書講解他的復(fù)原方法[3]。Nourse更沒想到的是這本書在1981年賣出了668萬本，成為當(dāng)年最暢銷的書籍。

Christoph?Bandelow 隨后也出版了一本書，介紹了魔方群的數(shù)學(xué)結(jié)構(gòu)[4]。Bandelow 還討論了魔方的變體，除了立方體形狀外還有正四面體，正八面體，正十二面體（五魔方）和正二十面體，這五個(gè)正多面體統(tǒng)稱柏拉圖立體(Platonic solids)，是全部的正多面體。

正多面體魔方有很多變化，比如二階魔方、四階魔方（Rubik’sRevenge）、五階魔方（Professor’s?Cube）,金字塔魔方（Meffert's Pyraminx）等等。?

二階魔方? Meffert's Pyraminx圖片來自文獻(xiàn)[4]?

 

1982年魔方無論是復(fù)原方法，還是數(shù)學(xué)理論，都有了很大進(jìn)展，除了一個(gè)重要問題還沒有解決，即Singmaster提出的上帝之?dāng)?shù)，也就是復(fù)原任意狀態(tài)的魔方所需最小步數(shù)的上界。Morwen B. Thistlethwaite給出了一個(gè)不超過52步的算法，將這個(gè)上界限制在52步以下。

大眾的狂熱沒有堅(jiān)持多久，到1982年底開始漸漸退去。對(duì)數(shù)學(xué)家來說，魔方把抽象的群論可視化，是非常好的教學(xué)和科研工具[5]。普林斯頓數(shù)學(xué)系教授曼紐爾·巴爾加瓦(Manjul Bhargava)在讀研究生的時(shí)候，經(jīng)常坐在宿舍里擺弄著一個(gè)特殊的二階魔方，魔方的8個(gè)角塊有八個(gè)字母a,b,c,d,e,f,g,h，代表8個(gè)整數(shù)，他覺得這個(gè)2×2×2結(jié)構(gòu)的魔方中隱藏著高斯復(fù)合問題(gauss composition)的秘密，努力地尋找答案。

無論是玩魔方，還是研究魔方，都離不開對(duì)魔方的標(biāo)記。Singmaster根據(jù)魔方每個(gè)面所處的位置用字母L(左面)、R(右面)、F(前面)、B(后面)、U(上面)、D(底面)表示，然后根據(jù)人們的操作習(xí)慣定義任意面順時(shí)針旋轉(zhuǎn)90度為基本操作，用各面字母的黑體L,R,F,B,U,D表示，逆時(shí)針旋轉(zhuǎn)90度則表示為L(zhǎng)',R',F',B',U',D'。

有了標(biāo)記后，描述魔方的旋轉(zhuǎn)就非常方便。比如L表示L面順時(shí)針旋轉(zhuǎn)90度，(L')2表示L面逆時(shí)針旋轉(zhuǎn)180度，DFD'F'表示從左至右依次執(zhí)行D、F、D'、F'操作。

魔方每個(gè)面有9個(gè)小正方形，六個(gè)面一共有54個(gè)小正方形，原始狀態(tài)下54個(gè)小正方形處在各自的位置上，對(duì)應(yīng)一個(gè)排列，不妨記作1，2，3，……，54。一個(gè)操作是一個(gè)置換，變換魔方上小正方形的位置，得到一個(gè)新的排列。理論上這樣的排列有54！（54！=1×2×3···×53×54）個(gè)，對(duì)應(yīng)54！個(gè)狀態(tài)。

實(shí)際上操作魔方得到的狀態(tài)遠(yuǎn)沒有這么多。54個(gè)小正方形分布在6個(gè)中心塊，8個(gè)角塊和12個(gè)棱塊上，如下圖陰影部分所示，每個(gè)中心塊分到一個(gè)小正方形，每個(gè)角塊有3個(gè)、棱塊有2個(gè)。

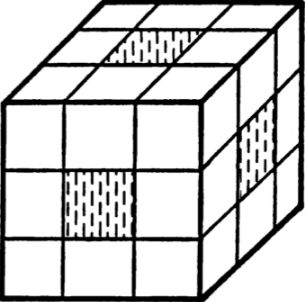
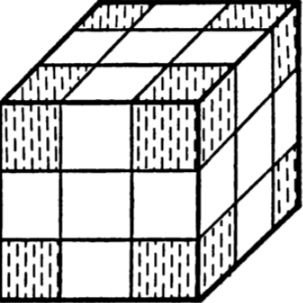
旋轉(zhuǎn)魔方的任意面，角塊和棱塊的位置發(fā)生改變，而中心塊位置不變。如果旋轉(zhuǎn)中心塊所在的中間層，等價(jià)于逆向旋轉(zhuǎn)相鄰的兩個(gè)面，因此理論上只需要考慮面的旋轉(zhuǎn)就行了。

6個(gè)位置不變的中心塊的顏色代表魔方各個(gè)面的顏色，從而魔方的狀態(tài)只由角塊和棱塊決定。由于角塊變到角塊，棱塊變到棱塊，因此8個(gè)角塊所有可能的位置有8！個(gè)，12個(gè)棱塊所有可能的位置有12個(gè)。

每個(gè)角塊的三個(gè)小正方形在角塊轉(zhuǎn)動(dòng)中可能產(chǎn)生順時(shí)針或逆時(shí)針旋轉(zhuǎn)，導(dǎo)致3個(gè)不同的定向，同樣每個(gè)棱塊會(huì)產(chǎn)生2個(gè)不同的定向(兩個(gè)小正方形的對(duì)換)，因此所有可能的狀態(tài)有8！×12！×38×212個(gè)，其中能夠由原始狀態(tài)通過操作魔方得到的狀態(tài)只有十二分之一，也就是8！×12！×37×210個(gè)，約 4.3×1019個(gè)。這些狀態(tài)稱為原始狀態(tài)的軌道，也就是全部的有效狀態(tài)。
五魔方有20個(gè)角塊，30個(gè)棱塊，有效狀態(tài)有20！×30！×319×227，約1068個(gè)，遠(yuǎn)遠(yuǎn)多于魔方。

群是一個(gè)常用的漢字，表示聚集在一起的人或物，數(shù)學(xué)上群被抽象成一個(gè)非空集合，集合中的元素可以是數(shù)，也可以是矩陣、置換等，并且還有一個(gè)單位元、每個(gè)元素有逆元，任意兩個(gè)元素之間服從一種運(yùn)算，滿足結(jié)合律且運(yùn)算結(jié)果仍然在集合中。全部整數(shù)的集合對(duì)于加法運(yùn)算就是一個(gè)群，0是單位元。

魔方中的很多操作都可以構(gòu)成群。比如由操作R得到的集合{R,R2,R3,I} 就是一個(gè)群，其中單位元是I，滿足R4=I。可以證明，魔方所有操作的集合構(gòu)成一個(gè)群，稱為魔方群。魔方群中的運(yùn)算是復(fù)合運(yùn)算，假設(shè)M1，M2是魔方群中的兩個(gè)操作，它們的復(fù)合M1M2表示對(duì)魔方先進(jìn)行M1操作，再進(jìn)行M2操作，有時(shí)復(fù)合運(yùn)算用符號(hào)表示為M1·M2。類似的，五魔方有五魔方群。

在2014年魔方誕生40周年之際，一篇發(fā)表的學(xué)術(shù)文章宣告了上帝之?dāng)?shù)的解決[6]，這個(gè)數(shù)是20，也就是從魔方的任意一個(gè)有效狀態(tài)恢復(fù)到原始狀態(tài)最多不超過20步（這里的一步使用half turn metric度量，指面旋轉(zhuǎn)90度或180度都算一步）。在這一年召開的國(guó)際數(shù)學(xué)家大會(huì)上，曼紐爾·巴爾加瓦獲得了菲爾茲獎(jiǎng)，委員會(huì)在介紹他的工作時(shí)寫到，“巴爾加瓦相信有更好的方法解高斯復(fù)合問題。然后有一天，他在玩魔方時(shí)，找到了答案。

參考文獻(xiàn)
[1]http://www.yau-awards.science/wp-content/uploads/2018/11/Gerald-Jiarong-Xupaper_1402.pdf
[2]David Singmaster，?Notes on Rubik's Magic Cube, 1981.
[3]James?G.?Nourse，The Simple Solutions to Cubic Puzzles，1981.
[4]Christoph?Bandelow, Inside Rubik's Cube and Beyond, 1982.
[5]J. Chen,?Group theory and the rubik's cube, Lecture Notes.
[6]Tomas Rokicki,et al.,The Diameter of the Rubik’s Cube Group is Twenty. SIAM J. DISCRETE MATH. Mathematics Vol. 27, No. 2, pp. 1082–1105.