2015PUPC普林斯頓大學物理競賽Onsite答案免費下載

歷年PUPC普林斯頓大學物理學術活動真題與答案免費下載

Onsite現場學術活動部分

翰林國際教育全網首發

力爭超快速發布最全資料

為你

千千萬萬遍

2015PUPC普林斯頓大學物理學術活動完整版真題免費下載

Onsite現場學術活動部分此卷共4題

但每題下分不同數量的小題

完整版下載鏈接見文末

2015PUPC普林斯頓大學物理學術活動完整版答案免費下載

部分真題答案預覽：

Question 1

a. The initial energy is

and the final energy is

For the ball not to lose contact,

Using conservation of energy, it follows that

b. A simple application of conservation of energy yields

or

Problem 2

Note that the moment of inertia of a uniformly distributed triangle with mass M and distance from center to vertex L is

a.??We apply conservation of angular momentum (about the center of the triangle), linear momentum, and energy. This gives

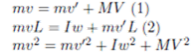
Subtracting L times (1) from (2) giveswhich we can substitute to get

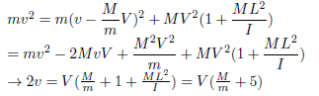
Substituting into (1) gives

Substituting into (2) gives

b.?In order for a second collision to occur, we need to consider v^/ relative to V (i.e. consider the motion of the point mass in the frame of the triangle). Clearly if v^/ >V , there will be no second collision since the point mass will ’escape’ the triangle’s reach -to see this clearly, draw the circle centered at the triangle’s center (i.e. the circumcircle of the triangle). The only possible point of contact for the second collision is at the bottom of this circle so the point mass must remain stationary relative to the triangle so that the triangle can rotate and collide with the point mass a second time.

Similarly, if v^/ <V , then there will be no second collision.

If v'= V , then indeed there will be a second collision since this means the point mass remains stationary relative to the triangle while the triangle will spin with angular velocity w> 0.

Thus, a second collision occurs if V = v^/ or 2m =5m ? M

M=3m

完整版真題資料可以底部二維碼免費領取↓↓↓

[vc_btn title="查看更多PUPC相關詳情" color="primary" align="center" i_icon_fontawesome="fa fa-globe" css_animation="zoomIn" button_block="true" add_icon="true" link="url:http%3A%2F%2Fwww.linstitute.net%2Farchives%2F26506||target:%20_blank|"]