AMC數學競賽考察哪些內容？不同體系的學生應該如何備考AMC？

AMC學術活動已經成為國際圈的熱門話題！近年來，國際學生紛紛咨詢AMC學術活動，雖然考試難度不如國內一些學術活動，但它確實有極高的含金量！

美國奧林匹克數學代表隊總教練表示，AMC成績是申請美國大學的“SAT3”，隨著越來越多的學生在SAT/SAT2的數學部分取得滿分，AMC成績在選拔學生中變得極為重要。該系列比賽在國際上聲譽卓越，許多中國留學生想要申請美國的頂級高中和大學，也會參加AMC系列學術活動，期望取得優異成績，讓申請簡歷更有亮點。

那么，AMC數學學術活動考察哪些內容呢？不同體系的學生又應該如何備戰呢？
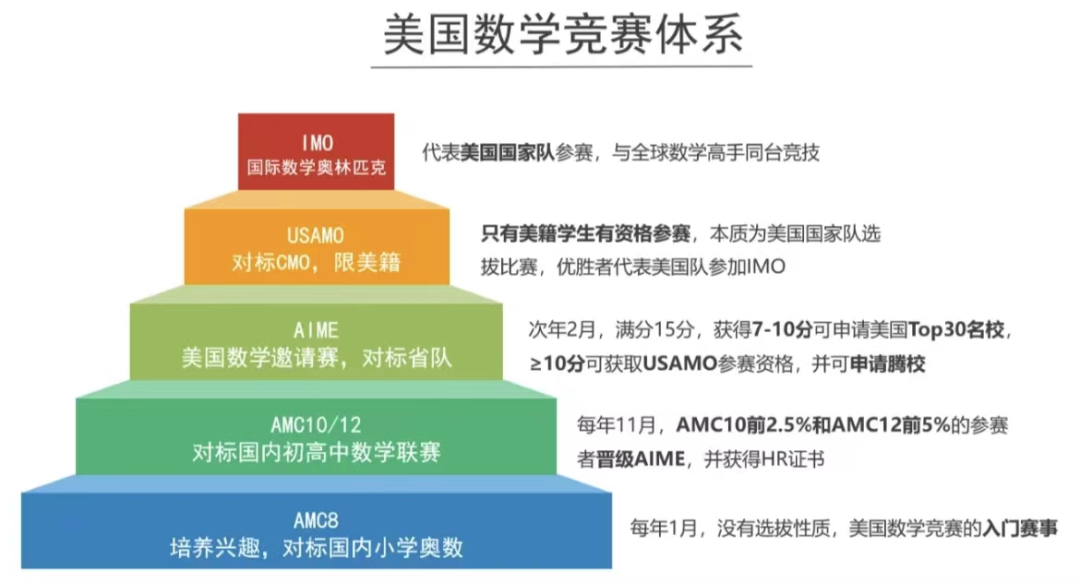從目前來看AMC是世界上可信度和效度最高的一個國際數學學術活動，普及程度非常廣，在全球有近百個國家的孩子熱衷于這個比賽，在各個國家甚至達到了幾千所學校，都會參加AMC數學學術活動。

AMC8考察范圍

基礎代數：整數，有理數，無理數，實數，數軸和直角坐標系;多元一次方程，簡單二次方程，簡單不等式；簡單數列；基本代數技巧。

基礎幾何：基礎幾何作圖；平面歐氏幾何，點、線、三角形、特殊四邊形、圓；規則圖形的周長和面積；基本平面幾何技巧；規則立體幾何圖形。

基礎數論：奇偶分析，整除的性質，最小公倍數和最大公約數，同余問題。

基礎組合：韋恩圖；排列、組合和概率入門；階乘和二項式系數，楊輝三角形。

AMC10考察范圍

進階代數：多項式，余數定理，韋達定理，根與系數的關系，特殊高次方程；進階不等式、均值不等式；函數入門，定義域和值域、二次函數、指數函數、對比函數、簡單三角函數；數列進階；代數技巧進階。

進階幾何：進階幾何作圖；三角形進階、正弦定理、余弦定理、內切圓和外切圓，斯圖瓦爾特定理，共點和共線；圓和四邊形，四點共圓，圓的外切四邊形；正多邊形，角度，周長和面積；進階平面幾何技巧；解析幾何入門。

立體幾何：點、線、面的關系，三維坐標系；立體幾何作圖；正多面體，歐拉公式；特殊的立體幾何圖形，立體幾何技巧。

進階數論：數，數組和序列；模運算，復雜同余問題；整數、分數和小數，進制轉換；基本丟番圖方程，進階數論技巧。

進階組合：容斥原理；二項式定理及相關結論；進階排列、組合和概率；期望入門，遞推、二分法，進階組合方法。

AMC12考察范圍

進階代數：復雜不等式、調和不等式、輪換不等式、柯西不等式;復雜函數問題，反函數和符合函數，三角函數和差化積、積化和差，萬能公式；復數，復平面，歐拉公式，蒂莫夫公式；數學歸納法、復雜數列和極限。

進階幾何：圓相關幾何進階；數形結合，二維、三維圖形的函數表達，進階解析幾何；不規則二維、三維圖形的處理；二維向量、三維向量。

進階數論：二次余數，高次余數、費馬圣誕節定理、費馬小定理；各類丟番圖方程的解法。

進階組合：隨機過程和期望；復雜組合問題技巧、基本綜合問題。

掃碼免費領取AMC資料包！包含近十年真題及解析！

領取報名表/咨詢報名注意事項/名師在線輔導！

不同體系應該如何備考AMC

IB體系學生備考

IB數學的課程體系分為2門4個等級：AA SL，AA HL，AI SL ，AI HL。這4門課程都分為5個topic：數與代數，函數，幾何與三角函數，概率和統計學，微積分。其中像三角函數、多項式、復數等部分，這些在AMC8/10/12學術活動考試中都是常考內容。

IB是AMC備賽最健全的一個體系，交叉內容很多，知識覆蓋面很廣，可以幫助學生打好基礎，但是IB數學的知識點的深度不夠，建議IB的同學們可以從AMC知識點的深度上下功夫。

A-Level體系學生備考

國內很多學校把IGCSE壓縮為一年，在IGCSE階段大量的詞匯學習已經幫同學們積累了英語詞匯量，在AMC學術活動備考時詞匯部分將會稍微輕松一些。

因為IGCSE數學考試里面的大部分考點都是國內學生在初中就掌握的很好的，比如：數字比較大小；因式分解；解一元一次、一元二次方程；勾股定理等。

AP體系學生備考

AP體系的數學課程內容主要是函數和微積分，AP體系的數學課程相當于大學數學2個學期的課程，AP整體側重點是微積分，其他的高中數學知識很少。

而AMC學術活動不考微積分，重點考的是數論和計數(這部分AP數學幾乎不涉及)，交叉的題型只有函數部分。所以，AP體系的學生是這幾個體系中最不占優勢的，AP體系的同學們是最需要AMC完整系統的培訓和輔導的。

普通體制內學生備考

對于普高黨來說，AMC是一個絕佳的證明自己的數學能力的機會。

AMC在美國的地位=中國的初聯/高聯，高聯課程知識點與AMC也有很大重合度，參加過高聯的學生可以多刷題，找薄弱點，針對性的補課，沒有學術活動基礎的學生則需要系統的訓練。

總的來說，IB體系和普通高中打過高聯的基礎比較好。這兩類學生需要評估自己的情況，然后再考慮備考方案。如果是普通高中沒有打過高聯或者是AP體系的學生，那么這些學生是處境比較困難的。這兩個體系的學生和AMC學術活動也沒有什么交集，必須要接受系統培訓。而A-level體系的同學處于中間位置，需要考慮兩種備考方案的可能性。