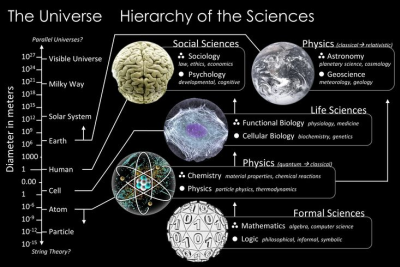
邏輯、分析、抽象思維，一起了解“數(shù)學(xué)”的魅力!

數(shù)學(xué)是利用符號(hào)語(yǔ)言研究數(shù)量、結(jié)構(gòu)、變化以及空間模型等概念的一門(mén)學(xué)科。作為人類(lèi)思維的表達(dá)形式，反映了人們積極進(jìn)取的意志、縝密周詳?shù)倪壿嬐评砑皩?duì)完美境界的追求。

雖然不同的傳統(tǒng)學(xué)派可以強(qiáng)調(diào)不同的側(cè)面，然而正是這些互相對(duì)立的力量的相互作用，以及它們綜合起來(lái)的努力，才構(gòu)成了數(shù)學(xué)科學(xué)的生命力、可用性和它的崇高價(jià)值。

基礎(chǔ)數(shù)學(xué)知識(shí)的運(yùn)用是個(gè)人與團(tuán)體生活中不可或缺的一部分。其基本概念的精煉早在古埃及、美索不達(dá)米亞及古印度的古代數(shù)學(xué)文本內(nèi)便可觀見(jiàn)。從那時(shí)開(kāi)始，其發(fā)展便持續(xù)不斷地有小幅度的進(jìn)展，直至16世紀(jì)的文藝復(fù)興時(shí)期，因著和新科學(xué)發(fā)現(xiàn)相作用而生成的數(shù)學(xué)革新導(dǎo)致了知識(shí)的加速，直至今日。

而今日，數(shù)學(xué)作為基礎(chǔ)的形式科學(xué)被廣泛的使用在世界不同的領(lǐng)域上，包括科學(xué)、工程、醫(yī)學(xué)和經(jīng)濟(jì)學(xué)等。所以被稱(chēng)為科學(xué)的皇后。

PART 1專(zhuān)業(yè)介紹

數(shù)學(xué)專(zhuān)業(yè)的學(xué)生研究數(shù)字、結(jié)構(gòu)和模式之間的關(guān)系。他們的課程范圍從代數(shù)到統(tǒng)計(jì)學(xué)，而且這些概念是相互關(guān)聯(lián)的。數(shù)學(xué)系的學(xué)生們會(huì)學(xué)習(xí)邏輯、分析、抽象思維和解決問(wèn)題等技能，這對(duì)未來(lái)的就業(yè)也很有價(jià)值。

數(shù)學(xué)專(zhuān)業(yè)的學(xué)生會(huì)學(xué)習(xí)代數(shù)、微積分、幾何和解決問(wèn)題所需的不同方程式。他們還學(xué)習(xí)如何思考并將這一基礎(chǔ)應(yīng)用于一系列更大、更復(fù)雜的問(wèn)題。

德國(guó)數(shù)學(xué)家卡爾-弗里德里希-高斯稱(chēng)數(shù)學(xué)為“科學(xué)的女王”，因?yàn)樗鼮槲锢憩F(xiàn)實(shí)帶來(lái)了許多啟示。一些學(xué)校區(qū)分了純數(shù)學(xué)和應(yīng)用數(shù)學(xué)。

描述這兩類(lèi)數(shù)學(xué)專(zhuān)業(yè)區(qū)別的一種方式是，應(yīng)用數(shù)學(xué)是將數(shù)學(xué)用于實(shí)際用途，而純數(shù)學(xué)更像是你可能在電影“Good Will Hunting”或“A Beautiful Mind”中看到的東西。

心靈捕手 Good Will Hunting

換句話說(shuō)，純數(shù)學(xué)是對(duì)數(shù)學(xué)本身的研究，沒(méi)有外部應(yīng)用的主要?jiǎng)訖C(jī)，但又并不代表純數(shù)學(xué)習(xí)到的東西無(wú)法拿來(lái)應(yīng)用。

PART 2專(zhuān)業(yè)分支

純數(shù)與應(yīng)用數(shù)學(xué)分支

純粹數(shù)學(xué)

純數(shù)-代數(shù) Algebra

01

代數(shù)是數(shù)學(xué)的一個(gè)分支，涉及到符號(hào)和這些符號(hào)的算術(shù)運(yùn)算。這些符號(hào)沒(méi)有任何固定值，被稱(chēng)為變量。在我們的現(xiàn)實(shí)生活問(wèn)題中，我們經(jīng)常看到某些數(shù)值在不斷變化。但是，我們一直需要表示這些不斷變化的值。在代數(shù)中，這些值通常用符號(hào)表示，如x、y、z、p或q，這些符號(hào)被稱(chēng)為變量。此外，這些符號(hào)通過(guò)加、減、乘、除等各種算術(shù)運(yùn)算進(jìn)行操作，目的是為了找到這些數(shù)值。

代數(shù)方程的表示

簡(jiǎn)單地來(lái)說(shuō)，代數(shù)就是研究運(yùn)算系統(tǒng)的學(xué)科，是一切關(guān)于計(jì)算的基礎(chǔ)，如果只是從表面來(lái)看，代數(shù)就是解方程，解的還是代數(shù)方程。不過(guò)代數(shù)遠(yuǎn)遠(yuǎn)不止如此，它更像是一門(mén)語(yǔ)言，給數(shù)學(xué)家用的語(yǔ)言，用以描述其他的數(shù)學(xué)事物，并且在研究量子力學(xué)的基本粒子，在考察剛體性質(zhì)和晶體結(jié)構(gòu)（群表示），在分析經(jīng)濟(jì)模式，在制造現(xiàn)代計(jì)算機(jī)等方面都是十分有用的。

純數(shù)-數(shù)理邏輯 Mathematical Logic

02

數(shù)理邏輯是數(shù)學(xué)的分支，研究的是一些非常專(zhuān)門(mén)的問(wèn)題。比如“決定性公理在ZF系統(tǒng)中的協(xié)調(diào)性與何種大基數(shù)等價(jià)”。這些知識(shí)對(duì)于日常的一般事物的“邏輯”分析沒(méi)有幫助。就像一個(gè)代數(shù)幾何專(zhuān)家不會(huì)更擅長(zhǎng)辯論一樣。

數(shù)理邏輯，其實(shí)是在用經(jīng)典概念的內(nèi)涵表示進(jìn)行計(jì)算，這個(gè)經(jīng)典概念的內(nèi)涵表示就是命題，而命題必須是可以判斷二值真假的陳述句這就是問(wèn)題的根源實(shí)際生活經(jīng)驗(yàn)中，大多數(shù)概念都是不能用命題表示的為了補(bǔ)足這個(gè)問(wèn)題，于是又有了概念的原型理論、樣例理論等等但數(shù)理邏輯依舊發(fā)揮著不可取代的作用像是蘊(yùn)含式這樣違背人類(lèi)直覺(jué)的東西，其實(shí)本來(lái)就不是設(shè)計(jì)給人看的，而是設(shè)計(jì)給機(jī)器看的，所以學(xué)好數(shù)理邏輯，也是為了計(jì)算機(jī)算法做鋪墊。

數(shù)理邏輯與算法的聯(lián)系

純數(shù)-拓?fù)鋵W(xué) Topology

03

拓?fù)涿枋龅氖蔷植啃巫兿碌牟蛔冃浴Ｅe個(gè)例子，對(duì)于拓?fù)鋵W(xué)家來(lái)說(shuō)，咖啡杯和面包圈沒(méi)什么區(qū)別。因?yàn)橹灰獔D形的閉合性質(zhì)不被破壞，在拓?fù)鋵W(xué)上它們就都是等價(jià)的。

拓?fù)鋵W(xué)家晨間例行公事

現(xiàn)代數(shù)學(xué)中有太多的結(jié)構(gòu)都離不開(kāi)拓?fù)洌負(fù)鋵W(xué)的基本內(nèi)容已經(jīng)成為現(xiàn)代數(shù)學(xué)工作者的常識(shí)，是現(xiàn)代數(shù)學(xué)的基本語(yǔ)言。

拓?fù)鋵W(xué)的重要性，體現(xiàn)在它與其他數(shù)學(xué)分支、其他學(xué)科的相互作用，就像拓?fù)鋵W(xué)在泛函分析（度量空間，Hilbert空間等都是拓?fù)淇臻g）、實(shí)分析、群論、微分幾何、微分方程等其他許多數(shù)學(xué)分支中都有非常廣泛的應(yīng)用。