簡單的三角函數及應用

涉及到A-Level或者Pre-Cal的數學，其中一個必學的內容就是三角函數(trigonometric function)。

今天，我們介紹一些簡單的三角函數的定義及應用，以便于同學們記憶和理解。

首先我們需要認識并且記住直角三角形(rectangle)里的每條邊的名稱：

對邊(opposite edge/side), 斜邊(hypotenuse)，鄰邊(adjacent edge/side)

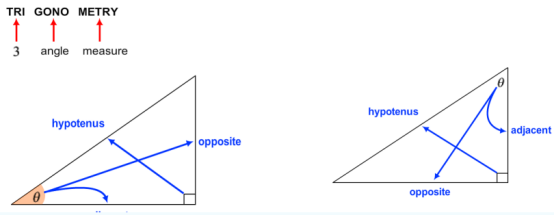
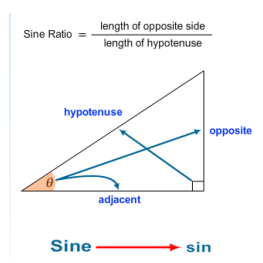
萬事俱備，我們首先定義正弦函數sin：

在直角三角形中，

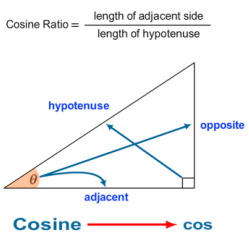
當然，還有我們經常用得到的余弦函數cos:

在直角三角形中，

 

當然，少不了的還有正切函數tan:

在直角三角形中，

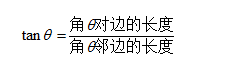
需要注意的是，之所以我們用到了比例(Ratio)一詞，因為三角函數的值,只取決于角Θ的大小，而不取決于直角三角形面積的大小。

 

涉及到三角函數的應用

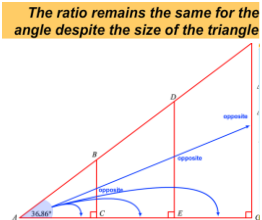
涉及到三角函數的一個簡單的應用是，已知直角三角形內若干條邊的長度，如何反推三角形的內角的大小。

例如下面一個例題：

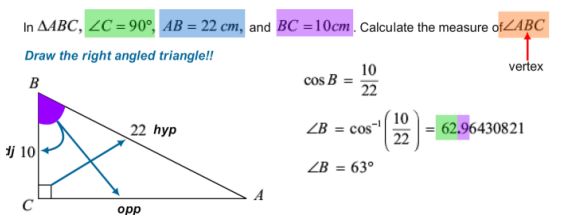
在直角三角形ABC中，角C是直角，斜邊AB的長度是22cm,直角邊BC的長度是10cm,求銳角B的大小。

分析：

在解決這個題的時候，很明顯地，我們可以通過斜邊AB和直角邊BC兩條邊的長度關系，同時利用到我們剛介紹過的三個三角函數sin、cos、tan的定義,得出cosB的具體數值。最后，我們可以利用手中的計算器中的cos﹣1這個功能，所得出的余弦數值為10/22的角度大小，即為我們想求得的銳角B的大小。

用數學文字表達出來的具體的解題過程，同學們可以參照下圖：

張老師今天再給同學們分享一個關于三角函數的比較復雜的應用題。

同學們可以先試著自己獨立解題。

如果在分析和解題過程中遇到困難，同學們可以依次參照下面三圖，

圖一、圖二、圖三分別按照分析和解題的邏輯順序，詳盡地解決了本題。

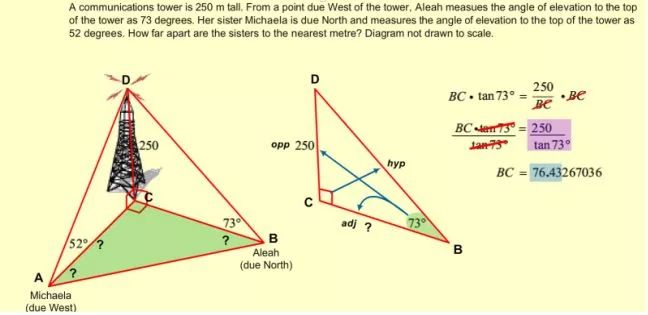
圖一

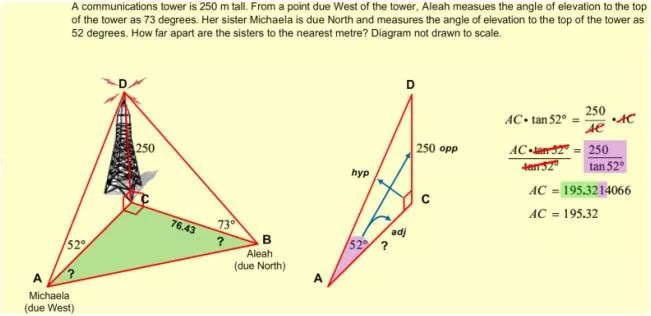
圖二

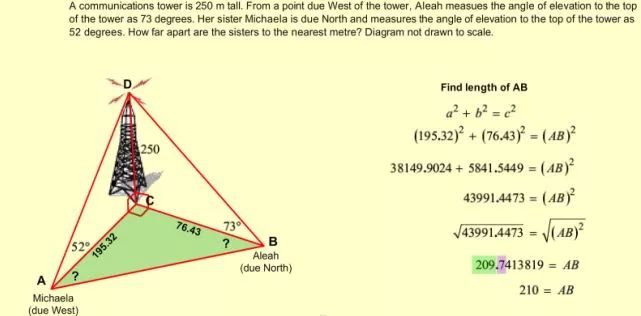
圖三

其實，定義三角函數并非必須先定義單位圓(unit circle)。我們今天學習的方式，是僅僅借助直角三角形，就簡潔地定義了正弦、余弦、正切三個三角函數。學好這三個基本的三角函數，并且相互之間不混淆，同學們就可以輕松地駕馭關于三角函數的更復雜的知識，做到觸類旁通啦~