奧數(shù)三十年：用1980年的人才觀 為2030年培養(yǎng)人才

這幾周，本來是華杯賽、希望杯等比賽舉行的日子。

不料教育部門一紙公文，各個比賽紛紛暫停或推遲。

在這個平靜的空檔期，正好可以和大家分享一些長一點、不那么急躁的東西。

近一年來，這些籠統(tǒng)的被稱為奧數(shù)的數(shù)學賽事始終處在輿論的風口，各種批評不絕于耳，主管部門的出手也越來越重。

從上海的叫停、成都的整頓、江蘇的“全面禁奧”，直到這一次，國家層面出了重手，徹底按下了暫停鍵。

在這場喧囂里，究竟誰犯了錯？

賽事的組織方錯了么？難道不應該給那些有天分、有才華的孩子提供發(fā)揮的舞臺么？不應該讓更多的人參與數(shù)學學習，感受數(shù)學的魅力么？

培訓機構(gòu)有錯么？數(shù)學學術(shù)活動又不是他們主辦的，題目也不是他們出的，他們教人知識，幫助考生提高成績，難道不對么？

莫非家長們錯了？他們在物質(zhì)和精神上作了巨大的犧牲，不就是想讓孩子考個好成績，上個好學校，奔個好前程么？

教育部門又有錯么？難道不應該讓大量的孩子從題海中解脫出來，有一個全面發(fā)展的空間么？

是生態(tài)出了問題。

在這個生態(tài)里，沒有人是贏家。

教育部門徘徊在姑息和越位的指責聲里；主辦方和培訓機構(gòu)被罵成了賺黑心錢的精神毒藥販賣者；家長在內(nèi)心的焦慮和錢包的縮水中掙扎，而孩子是上不完的培訓班，做不完的題目。

即使那么得了獎、得以進入某名校的孩子，就是這場賭局的勝利者么？以他們驚人的天賦和刻苦的投入，他們不應該把目標放高一點，去做那些更能幫助他們成為下一個史蒂夫?喬布斯或者埃隆?馬斯克的事情么？

看到今天奧數(shù)面對的巨大爭議，我們很難想象它在興起之初，卻充滿了寄托和情懷。

奧數(shù)三十年 從情懷到毒藥

在一場運動中虛耗了整整十年后，中國數(shù)學界在運動剛剛停歇之際，就迫不及待的組織起面向中學生的數(shù)學學術(shù)活動來，希望在學術(shù)活動中找到一些好的苗子。

這樣的選拔方式在國家的肯定下，逐步擴大開來，形成了固定的模式。

（1978年數(shù)學學術(shù)活動資料及華羅庚的題詞）

1986年開始舉辦的華羅庚杯，以這位充滿傳奇色彩的數(shù)學家、同時又是數(shù)學學術(shù)活動的大力倡導者命名。

華杯賽的賽名，由領(lǐng)導人親筆題寫，時任國家科委主任方毅任首屆杯賽的組委會主任。

出題的5位數(shù)學家，有清華北大的教授，也有后來的院士、博導。

這個國家以這樣的方式，來表達對知識的尊重和對人才的渴求。

隨后的十幾年里，盡管奧數(shù)也有普及和發(fā)展，但始終局限在小范圍學生參加的智力學術(shù)活動。

家長們甚至擔心，在奧數(shù)上花太多時間，會影響主科上的成績。

奧數(shù)真正進入膨脹期，是在90年代末小升初統(tǒng)一考試取消之后。

小升初考試取消后，奧數(shù)由于良好的辦賽基礎(chǔ)和普及程度，以及恰到好處的拉分效果，迅速填補上了空檔，成為小升初考試的第一替代品。

奧數(shù)比賽的內(nèi)在邏輯由學有余力變成了小升初的敲門磚，參與奧數(shù)比賽的效費比徹底改變，由此走向了全民奧數(shù)。

人們很快發(fā)現(xiàn)，如果花少量的時間，系統(tǒng)學習奧數(shù)題目的解題技巧，就可以在考試中占據(jù)很大優(yōu)勢。

于是，對奧數(shù)培訓班的需求迅速釋放，而蓬勃興起的培訓班又再次推動了奧數(shù)的普及。

參與的人數(shù)越來越多，奧數(shù)培訓越來越普及，參與者的水平也越來越高，但獎項只有那么多，只好進一步分層。

于是，奧數(shù)的題目不得不出得越來越難，越來越偏，考生需要記住越來越復雜的技巧，僅僅在小升初前一兩年接受培訓已然沒什么優(yōu)勢。

結(jié)果，孩子們不得不上更多的培訓班，做更多的題，開始學習奧數(shù)的年齡也一再下探，開啟了一個“題目變難——上更多的培訓班——水平提高——題目更難”的循環(huán)。

在這場奧數(shù)運動中，獲利頗多的培訓機構(gòu)，開始由最初的參與者、協(xié)作者，逐漸變成了賽事的組織者、主辦者，獲得了越來越大的話語權(quán)，也多次引發(fā)了對學術(shù)活動公平的質(zhì)疑。

這樣的內(nèi)在邏輯不改變，即使受到多次整頓打壓，奧數(shù)學術(shù)活動反而不斷壯大，甚至形成了穩(wěn)定的心理預期，所謂整頓不過是一陣風而已，等過了風頭，換個頭面，該干嘛干嘛。

如此越挫越勇，在過去十幾年，恐怕也只有房地產(chǎn)業(yè)可以一比。

房市里，上車了的都成為了贏家。

但在奧數(shù)學術(shù)活動里，大多數(shù)人終究是陪跑者。

即使如此，在升學的壓力面前，奧數(shù)仍是非上不可。

別人不上我上了，占便宜；別人上了我也上，不吃虧，全民奧數(shù)最終成為了無人可以擺脫的囚徒困境。

（2009年，北理工教授楊東平在他的博客上，喊出了“打倒萬惡的奧數(shù)教育”，引發(fā)了圍繞奧數(shù)的又一次論戰(zhàn)）

如果僅僅因為一項學術(shù)活動難度高、參與人數(shù)多、投入巨大、功利性強而指責它，顯然是難以服眾的。

奧數(shù)最要命的問題，不在于這些外在的喧囂，而是它本身內(nèi)在的問題：學奧數(shù)到底對培養(yǎng)人才有什么好處？有沒有好處？

在說奧數(shù)之前，我們先來說說，數(shù)學應該是怎樣的。

兩種數(shù)學

數(shù)學的教科書上寫的解答，總是很有條理，把最優(yōu)的方法告訴我們，又沒有什么廢話。

但我們自己做題的時候，卻很難這樣從容。

往往要這里試試，那里試試，在有一點進展之前，總要試過幾個愚蠢的想法，有時憋了好幾天，仍然束手無策。

即使勉強把題目做出來了，也要反復謄寫幾次，才能寫得比較簡略和精確，更不用說是不是最佳的方法了。

波利亞把這種差別，形象的叫做“兩種數(shù)學”。

一種是教科書上的數(shù)學解法，它是演繹的、簡潔的、完整的、系統(tǒng)的和最優(yōu)的。

另外一種是我們尋找數(shù)學解法的過程，它是探索的、繁冗的、斷續(xù)的、碰運氣的，但又是充滿生氣和創(chuàng)造力的。

這“兩種數(shù)學”也發(fā)生在數(shù)學的課堂上。

日本數(shù)學教育家米山國藏在其《數(shù)學的精神、思想和方法》一書中，以三角形內(nèi)角和為例，詳細的講了他理想中的數(shù)學課堂。

米山說，在教學三角形的內(nèi)角和時，一般的幾何書會先給出“三角形的內(nèi)角和等于180度”這個命題，再給出證明。

學生縱然學到了這一幾何知識，甚至還記住了證明的步驟，但他們完全不知道這個命題是怎樣來的，也不知道研究的過程和方法，更不用說培養(yǎng)了什么用于研究和發(fā)現(xiàn)的內(nèi)在素質(zhì)了。

米山認為，這堂課應該這么教：

首先是實驗，讓學生們動手測量三角形的內(nèi)角并求和。

為了讓學生明白實驗的目的，測量的工作和方法要盡可能精確，測量的結(jié)果才能盡量準確。

實驗的結(jié)果，可能大部分學生測得了180度，也會有一部分學生測得181度、179度或者其他結(jié)果。

這時，老師應引導學生猜測，三角形的內(nèi)角和等于180度，但同時讓他們注意，他們只是在很少的一部分三角形中測到了180度，不能由此判定，任意三角形的內(nèi)角和都是180度。

實驗是用來提出問題的。

不做實驗，三角形內(nèi)角和等于180度這個推測就無從而來。

有了推測，還要完成相應的證明過程。

證明的構(gòu)想也可以從實驗中來。

把一個三角形的三個角減下來拼在一起，正好可以拼成180度。

由此可以聯(lián)想到添加平行線作為輔助線的方法，可以把任意三角形的三個角“拼”在一起，來證明這一命題。

實驗和證明是數(shù)學方法的兩翼，相輔相成。

但學習不應到此為止。

老師可以接著提問：凸四邊形的內(nèi)角和等于多少度？他可以讓學生用實驗的方法，也可以用證明的方法來解答。

如果學生們沒能自己發(fā)現(xiàn)的話，還應該提示他們，可以把凸四邊形的問題和三角形聯(lián)系起來，把凸四邊形分割成三角形，引用上述三角形內(nèi)角和的定理來解題。

接著，再來求凸五邊形、凸六邊形的內(nèi)角和，此時學生應會想到，直接應用三角形的內(nèi)角和來計算凸五邊形的內(nèi)角和。

一旦老師啟動了探索的第一步，就可以讓學生們來主導發(fā)現(xiàn)的過程，老師只需要適當?shù)耐扑麄円话选?/p>

讓他們算一算凸10邊形、凸100邊形、凸1000邊形的內(nèi)角和，直至一個一般性的問題：一個凸n變形的內(nèi)角和。

把三、四、五、六邊形的內(nèi)角和寫出來，就容易看出這是一個以180度為公差的等差數(shù)列，再用推理的方法證明就可以了。

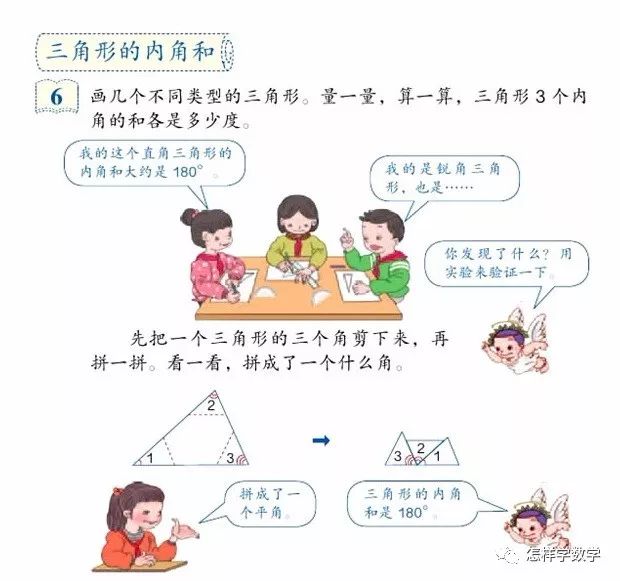（我國現(xiàn)行的教材一般會在小學階段通過實驗得到三角形內(nèi)角和的結(jié)論，在中學階段完成證明部分。

和米山國藏的設(shè)想相比，數(shù)學方法上的討論似乎不夠充分。

）

絕大多數(shù)的學生，都不會在他們畢業(yè)之后再用到三角形內(nèi)角和這一定理。

如果只把單純的用不上的知識交給學生，學生學到的只是數(shù)學的僵尸，以至于讓他們認為數(shù)學完全沒有意義，學數(shù)學只是為了分數(shù)。

這是我們說的第一種數(shù)學。

只有教會學生發(fā)現(xiàn)和研究，數(shù)學才是有生氣的東西。

即使數(shù)學課上學的知識完全用不上，但他們學到了發(fā)明、發(fā)現(xiàn)和創(chuàng)造的種種方法，培養(yǎng)了應用能力、邏輯推理能力和想辦法的能力，這樣的方法深刻的留在他們的腦子里，在今后遇到現(xiàn)實的問題時，能夠隨機應變。

并且，學生始終理解課程的意義，對課程充滿興趣，更可能在長期乃至終身的學習中取得成功。

這是我們說的第二種數(shù)學。

但這樣講課，同樣的內(nèi)容進度要用去多得多的時間。

一堂課能灌輸完的內(nèi)容，需要四、五堂課才能講完。

況且，幾十人的大班上很難進行充分綿密的思考和討論，只有將學生分成至多七、八個人一組的小組，才能得到比較好的效果。

所以，即使不考慮那些真正理解數(shù)學、能夠創(chuàng)造性組織課堂的老師比那些只會照本宣科的老師要稀缺的多，僅就數(shù)量而言，需要投入的教育資源就有十幾倍乃至幾十倍之差。

所以，米山無奈的承認，能夠按照他的設(shè)計來教課的教育工作者，實在是太少太少了。

少即是多

如美國數(shù)學家David Klein所說，數(shù)學教育中最大的矛盾，是內(nèi)容和方法的矛盾。

這一說法咋一看不可思議，內(nèi)容是教什么的問題，方法是怎樣教的問題，這兩者就像人的兩足，缺一不可，又怎么會矛盾呢？

問題恰恰出在，到底應該是以內(nèi)容優(yōu)先還是方法優(yōu)先。

如果以內(nèi)容優(yōu)先，就必然要用灌輸?shù)姆椒ǎ瑢W生可以記住足夠多的知識，并且在考試中有好的表現(xiàn)。

但如果想要鼓勵和調(diào)動學生的參與，以他們能力的成長和長期的潛力作為優(yōu)先的目標，這樣的課堂就要比灌輸?shù)恼n堂多花費幾倍的時間，就必須減少學習內(nèi)容，以犧牲內(nèi)容的量為代價。

也就是說，少即是多。

內(nèi)容講的少了，但是學生參與多了，思考多了，興趣多了，課堂的強度不但不少，反而更大。

只有離開應試，數(shù)學才會是生動的，漂亮的，充滿創(chuàng)造力的。

否則，就一定會陷入灌輸、強記和題海戰(zhàn)術(shù)的泥潭。

如果高考制度難以改變，以高考為目標的應試教學無法避免，那么能不能在義務教育階段，減少一些應試的成分，多關(guān)注一些能力的培養(yǎng)呢？所以，在多次的課改之后，數(shù)學課本上的知識點少了、淺了，怎樣發(fā)現(xiàn)和解決問題的東西多了。

即使在實施中，這些改變還沒有達到預期的效果，也出現(xiàn)了一些教條和形式主義的東西，但是總的來說，課改的努力是可以看見的。

但學校教育無法解決大班上課的問題，或者說，以公共的教育資源，只能做到這種程度了。

那么，在學校之外，在家長和學生可以自己選擇的地方，是不是可以讓孩子們吃些細糧，消化消化呢。

可惜，奧數(shù)的泛濫毀掉了課改的努力。

犀鳥的盔 極樂鳥的羽

在學校課堂上，哪怕教師最終關(guān)注的是分數(shù)，他們也得按照教材的要求，把起碼的過程和方法給學生講一講。

但為學術(shù)活動成績而生的奧數(shù)課堂卻沒有這些束縛，它就像脫韁的野馬，迅速異化成了應試的機器：就是用多快好省的手段，通過大量的記憶和模仿，迅速積累特定問題的解題技巧。

舉一個例子。

求格點面積是三年級的學生經(jīng)常遇到的一類問題。

在格點中，學生可以直觀的看出三角形的面積是怎樣和長方形聯(lián)系起來的。

這樣的問題是幾何學習中的重要一環(huán)，可以幫助學生由已經(jīng)學會的長方形面積公式過渡到三角形。

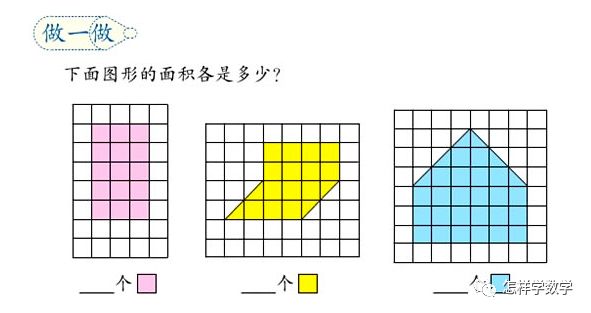（人教版教材上的求格點/網(wǎng)格面積問題）

如果把基礎(chǔ)的格點面積問題稍作變化，可以變成下面這樣求格點面積的問題。

解這樣的問題，要把圖形作適當?shù)姆指睿殖扇舾蓚€已學會的基本圖形，分別求出各部分的面積后再求和。

這樣的題目，可以鍛煉學生的平面觀察和想象力，還包含了一種樸素但是關(guān)鍵的數(shù)學思想：如果把一個未知的問題轉(zhuǎn)化成一個已知的問題，這個問題就解決了。

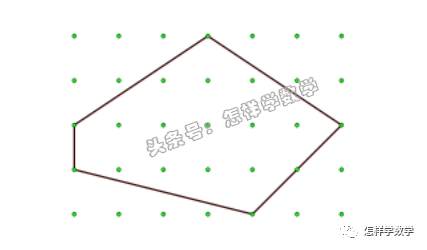這樣的題目，出現(xiàn)在課外的練習冊上，讓學生們做一做，不是很有好處么？

但是在奧數(shù)班上，正確率和解題速度才是唯一的目標，學生們就會被告知應該按照以下方法來解題：

根據(jù)皮克公式，格點的面積等于圖形內(nèi)的格點數(shù)加上圖形邊上格點數(shù)的一半再減1，本題中，圖形內(nèi)的格點有12個，圖形邊上的格點有6個，所以，圍成的面積等于12+6÷2-1=14個單位面積。

這種解法里，學生們根本不知道皮克公式是怎么來，也不理解它為什么正確。

但是這樣解題，又快正確率又高。

好笑的是，當學生升入五六年級，格點圖形變成圓形、扇形的組合圖形后，他們就不能再使用皮克公式了，又回到圖形分割拼補的老路上。

這樣拿來就用、用完就扔的所謂“方法”，在奧數(shù)中比比皆是。

如果這個例子講的是奧數(shù)里野蠻暴躁的“多講”，那么下一個例子就是不能自圓其說的“少講”。

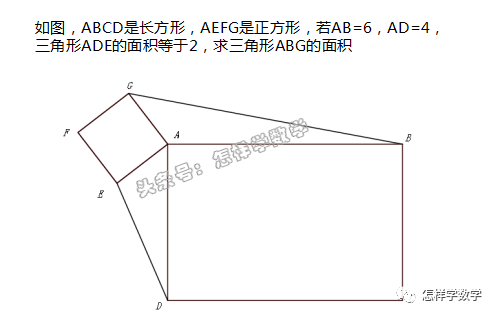解這個問題，需要證明下圖所示的兩個陰影三角形全等。

對于學過公理化證明方法的中學生來說，這并非難事。

但小學生應該怎樣證明呢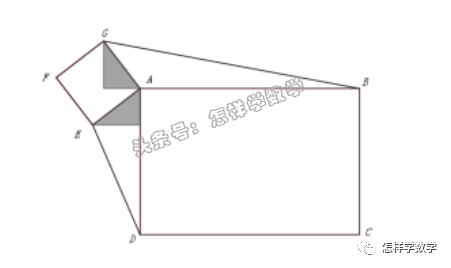？ 只需簡單一句話：這兩個三角形旋轉(zhuǎn)后重合。

如果兩個三角形看起來是一樣的，就認為它們是一樣的，這樣的做法，不是和數(shù)學最基本的精神背道而馳嗎？

要解決這個問題，需要引入一些中學的平面幾何內(nèi)容。

對于那些基礎(chǔ)和能力都很好的學生，提前教給他們一些真正有用的東西，也未嘗不可。

奧數(shù)為什么又反常的自我限縮，寧可在一些過于初等甚至說不通的方法里打轉(zhuǎn)呢？

“多講”和“少講”的這兩個例子，反應了奧數(shù)真正的問題。

它是按照上世紀80年級的人才觀、知識觀設(shè)計的智力游戲，它無視時代的變化，也缺少對自身真正價值的內(nèi)省。

學的東西是不是學生需要的，不知道。

學生在其中可以獲得哪些能力成長，不清楚。

甚至連所學的是有害還是有益，都可以假裝看不見。

只要能夠打造并維系一個名利場，自然有人買單。

有些種類的犀鳥在頭部長有巨大的盔狀突起，就像頭盔一樣。

這些笨重的盔突沒有任何實際的作用，反而影響了犀鳥的飛行，其明亮的顏色也更容易引起捕食者的注意。

類似的例子還有極樂鳥漂亮但無用的尾羽，一些鹿細致的、明顯超過了打斗需要的角。

（長著夸張盔突的冠斑犀鳥）

這樣的現(xiàn)象曾讓達爾文大為不解，它們看起來和自然選擇格格不入，為什么自然選擇會保留這些對生存競爭完全無用乃至有害的構(gòu)造呢？

達爾文最終認識到，這些構(gòu)造并不是對他的學說的挑戰(zhàn)，反而可以用自然選擇完美的解釋。

只有那些強健的個體，才能帶著巨大的盔突，在殘酷的生存競爭中存活下來。

盔突越大、越明亮，越能證明個體的強健，也越容易獲得異性的青睞和選擇，使得這種基因在后代中保留和積累下來。

奧數(shù)金牌，就是我們這個叢林的盔突和尾羽。

中國版的“新數(shù)運動”

上世紀50年代末，美國教育界興起了一場“新數(shù)運動”（New Math），他們對K12階段的數(shù)學課做了徹底的改革，以提高中學畢業(yè)生普遍低下的數(shù)學水平。

“新數(shù)運動”最終徹底的失敗了。

發(fā)起者們過于想教育學生“數(shù)學是什么”，而多少忽略了“數(shù)學該怎樣學”。

新的教材和課程難度太大，甚至有些一線的教師也不能完全理解。

“新數(shù)學”也成了激烈但不切實際的改革的代表。

在不同的時空背景下，我們需要一場意義完全不同的“新數(shù)運動”：我們需要新的數(shù)學，也需要一場運動來實現(xiàn)它。

新的數(shù)學是更現(xiàn)代化的數(shù)學和數(shù)學課。

它具體是什么樣的，我們在上面已經(jīng)舉了一些例子。

今天的K12教育是培養(yǎng)2030年的人才，他們不需要累積解數(shù)學題的技巧，而需要用所學解決問題的能力。

之所以說是一場運動，是因為“新數(shù)學”遠不止在課堂之內(nèi)，更要更新社會公眾對數(shù)學的認識。

數(shù)學課是什么樣的，并不是由其供給者——數(shù)學家和教育工作者——決定的，而是基于供給者和需求者——家長和學生——的共識。

否則，家長們就會用腳投票。

家長們固然關(guān)心長期的能力成長，但他們也重視短期的成績和排名。

在分數(shù)之外，需要有較為公平和有效的評估數(shù)學能力的方法，把真正的數(shù)學能力和針對測評的包裝和投機取巧區(qū)分開來。

否則，奧數(shù)的陰影仍會重來。

“新的數(shù)學”需要資源投入，需要大量精細的基礎(chǔ)工作，需要時間的淬火和檢驗，更需要每一個關(guān)心孩子成長的家長和教育工作者的參與。

我們歡迎你把這樣的觀點傳播給更多的人，也歡迎把你的意見大聲的告訴我們。

除了坐而談，更要起而行。

我們會在我們的實驗課上，實踐“新的數(shù)學”的設(shè)想，檢驗和完善它。

目前即將增開的是三年級的思維課和四年級的內(nèi)容課。

如果你有興趣，請聯(lián)系我們。