- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
AQA A Level Physics復習筆記7.2.2 Calculating Gravitational Potential
Calculating Gravitational Potential
- The equation for gravitational potential?V?is defined by the mass?M?and distance?r:
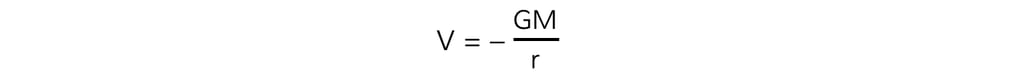
- Where:
- V?= gravitational potential (J kg-1)
- G?=?Newton’s gravitational constant
- M?= mass of the body producing the gravitational field (kg)
- r?= distance from the centre of the mass to the?point mass?(m)
- The gravitational potential always is negative near an isolated mass, such as a planet, because:
- The potential when?r?is at infinity (∞) is defined as 0
- Work must be done to move a mass away from a planet (V becomes less negative)
- It is also a?scalar?quantity, unlike the gravitational field strength which is a?vector?quantity
- Gravitational forces are always?attractive, this means?as?r?decreases, positive work is done by the mass when moving from infinity to that point
- When a mass is closer to a planet, its gravitational potential becomes smaller (more negative)
- As a mass moves away from a planet, its gravitational potential becomes larger (less negative) until it reaches 0 at infinity
- This means when the distance (r)?becomes very large, the gravitational force tends rapidly towards 0 at a point further away from a planet
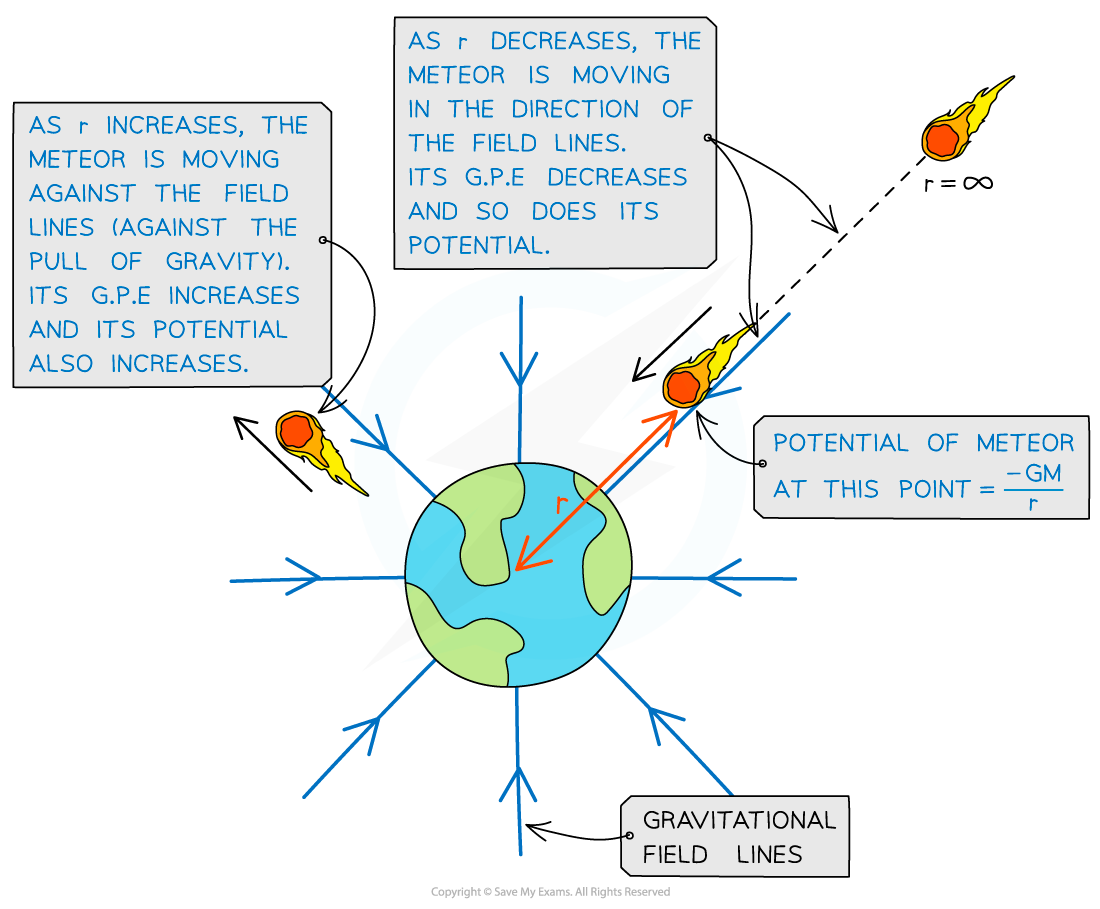
Gravitational potential increases and decreases depending on whether the object is travelling towards or against the field lines from infinity
Worked Example
A planet has a diameter of 7600 km and a mass of 3.5 × 1023 kg.A rock of mass 528 kg accelerates towards the planet from infinity.At a distance of 400 km above the planet's surface, calculate the gravitational potential of the rock.
Step 1:?Write the gravitational potential equation
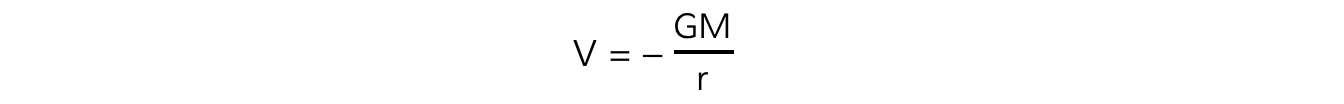
Step 2:?Determine the value of r
-
- r is the distance from the centre of the planet
Radius of the planet = planet diameter ÷ 2 = 7600 ÷ 2? = 3800 km
r = 3800 + 400 = 4200 km = 4.2 × 106?m
Step 3:?Substitute in values
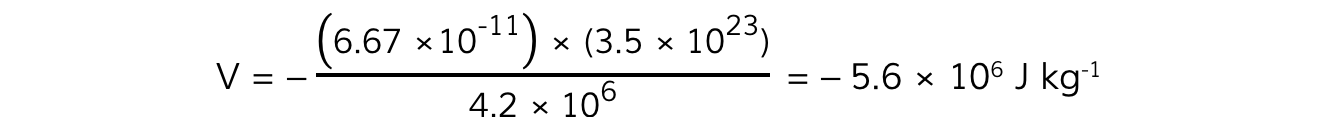
Exam Tip
Remember to keep the negative sign in your solution for the gravitational potential at a point. However, if you’re asked for the ‘change in’ gravitational potential, no negative sign needs to be included since you are finding a difference in values and just the magnitude is normally required.Remember to also calculate?r?as the distance from the?centre?of the planet, and not just the distance above the planet's surface
轉載自savemyexams

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









