發刊詞 | 用動圖讓你直觀理解數學中的定理

圖在數學中不算新的東西，不論在任何文化中，自從有了數字就有了圖。

比如，表示1這個數字，可以畫一條線表示，表示2這個數字，就畫兩條線。

當人們發現100，1000這樣的數字用畫一百一千根線很麻煩的時候，便發明了進制：用一種特殊的圖，表示100，1000等等，這是圖和代數的聯系。 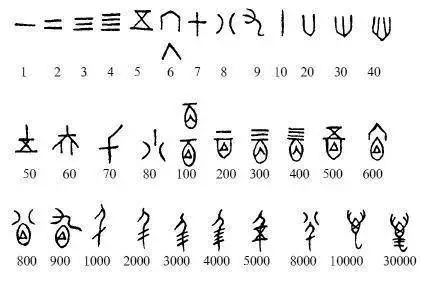圖和幾何的聯系更多。

無論是中國的《周髀算經》還是外國的《幾何原本》，在講幾何的時候必定會畫圖。

或者說，圖就是一種數學語言，它在數學中的重要性絲毫不低于數字和字母，以至于平面幾何、解析幾何、立體幾何貫穿整個中學數學。

說到中學數學教學，大家會想到中學時代老師在黑板上畫著各種圖形，寫著各種公式。大家有沒有遇到這種情況，老師說：“看，這條線長度恒過這一點”

“看，這個比值算出來一定是2”

大家腦子里卻對這個“恒等于”“頂點”的問題沒有一個直觀的感覺，好像只是算出來的，不是看出來的。一、二十年前數學教學是這樣可以理解，但2018年的今天，我們的數學基礎教學在很多地方依然是這樣講這樣學，很多學生覺得不好直觀理解的東西依然不好理解。我就在想，我做什么

能幫助正在初中入門數學的學生直觀的理解這些概念？答案就是：學數學到底是在研究什么？在我看來，是研究數字之間的連系和圖形之中的變換。如果大家能能預先對于這個過程有個直觀的印象，再去證明和記憶就不難了。現在數學教學中就缺乏一個直接能看到的過程。我來舉個例子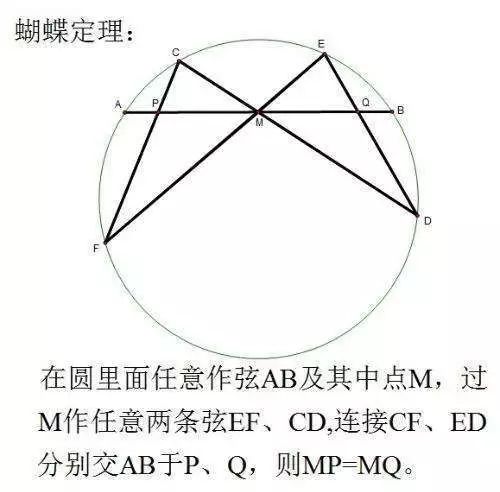：上圖是傳統的教學方法：這個定理首先有三步作圖過程，做出線段MP和MQ后，大家對它的長度是不是一定相等的不確定，看到結論說的是相等，云里霧里地就著手去證明，忽略了一個更重要的事：讓學生親眼看到相等。

只有親眼看到了無論圖形怎樣變化結論都是成立的，才能把這個知識直觀的理解，而非死記硬背。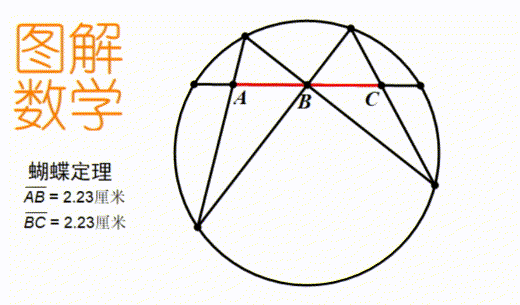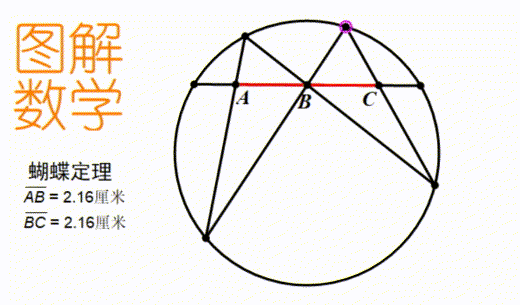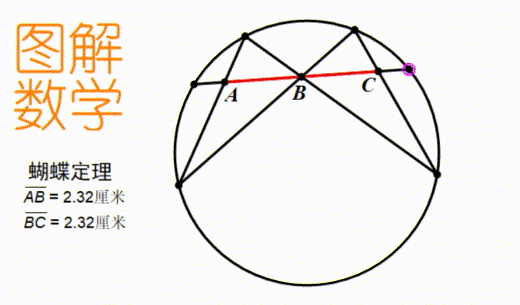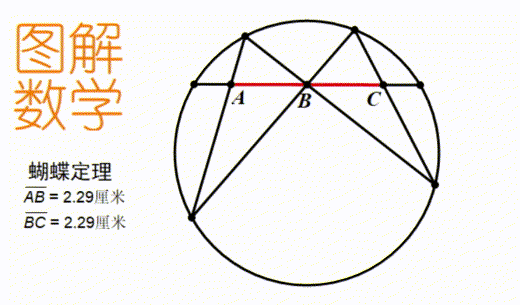動圖是我提倡的數學學習新工具。它既不像視頻那么麻煩，又不像定圖那樣只能反映一個時刻的信息。比如上圖，我們可以直觀地看到，無論這三條弦怎么變化，測量出的AB和BC的長度永遠都一樣。

這種變化中的不變性，正是數學里要研究的。所以，花幾秒鐘看這個動圖，比對著定圖

記憶十幾分鐘都有用。這也正是我所想的，2018年的數學教學應該比一二十年前進步的地方。

當然，證明過程也是不可替代的。

其他學科，比如物理化學，研究方法是：如果做實驗出來結果符合理論，那么理論就是對的。

而數學的研究方法是：即使舉出一千個一萬個圖形是對的，也不能充分地說明這個定理是對的。想說明一個定理的正確性，要靠嚴謹的證明。

《圖解數學》系列每個定理都會告訴大家如何證明。