AMC12數學競賽試題解析！

AMC在知識點的儲備上其實并沒有超過初高中生的能力范圍，所有的AMC考題無論是簡單題還是難題、超難題可以說100%都可以使用同學們現有的知識去解決。以這道AMC12數學學術活動試題解析為例，想要在AMC考試中異軍突起，拿到AIME的入場券無非在于下面兩項比較重要的能力：

1.掌握更多的數學知識

比如calculus，比如matrix，比如complex plane。往往一道比較“難度”的題目，其實只是某種高階知識的基礎性題目; 一道很難用疊加概率算出的題目，calculus的定積分思想簡直就像“一鍵解題”。

2.改變以往的數學思維模式，提高解決問題的技巧

大部分同學可能并沒有時間去學習calculus，linear algebra，complex plane等等稍微偏離高中基本數學基礎的知識，那么這個時候我們在做AMC題目的時候一定要有一個這樣的一種認知：“數學學術活動只要解決問題即可，不需要得到類似于1+1=2的定解”，怎樣快速并相對準確得到我們想要的答案將是AMC備考大家要掌握的核心技能。

這里我們給大家舉個例子讓同學們感受一下，其實一道毫無頭緒的“難題”我們也是可以利用初高中知識飛速暢快解題的：

我們看下這道2017年A卷的第15題，需要我們確定多個三角函數疊加在一起的函數的第一個positive root，“普通”同學可能直接懵逼，“大佬”同學們心里想的是這個：

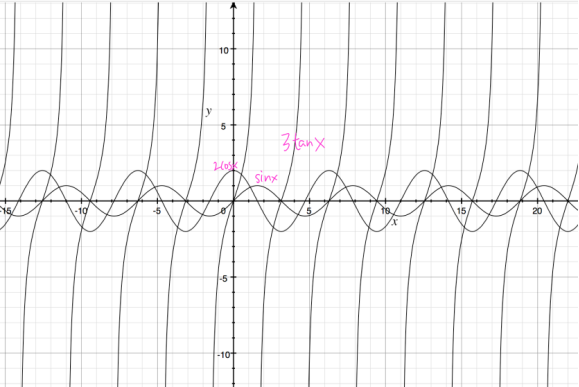
在嘗試了半天構建三者在疊加在一起的函數尋找零點后宣告放棄。更有“奇葩”同學宣稱一定要找到這個zero point的exact value，做了如下嘗試：

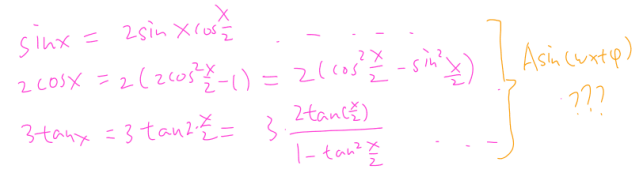
然后就沒有然后了。

其實無論是哪種同學的第一反應我們都能夠理解，往往在尋找零點的時候，大家已經習慣了用計算器去尋找，或者把它化成我們熟悉的函數再去用公式求解。但其實這道題大家只要擁有對sinx、cosx、tanx角度轉動的基本了解以及按照“零點左右發生正負改變”的思路去想就能夠秒出答案：

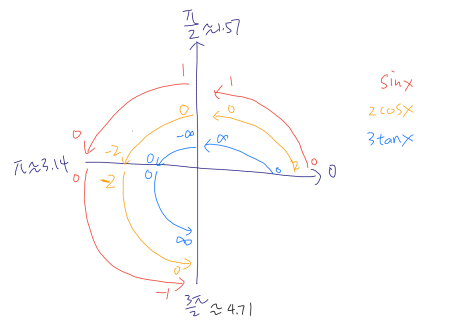
我們可以看到其實大家要做的只有兩件事：

確定這三個函數在第一、二、三qudrant的函數值變化情況，可以看出在first quadrant三者疊加always positive，在second quadrant三者疊加alway negative，在third quadrant三者的疊加出現了“正負交替”，from -2 to positive infinity.

因此第一個zero point 一定出現在third quadrant，但是因為third quadrant的radians是從3.14到4.71，我們無法用該信息排除其中任一選項，那么下面我們可以選取一個相對熟悉的角比如(5pi/ 4)來做下區分：

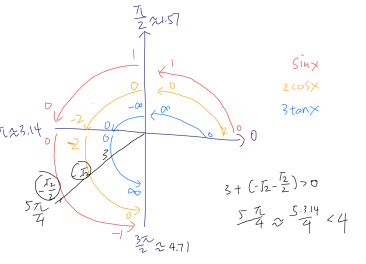
這里我們可以看出在(5pi/4)處，三個函數的疊加值是大于0的也就是說在這個角度之前就發生了正負的交替，并且(5pi/4)是小于4的，那么我們就完全確定了在3到4之間發生了正負交替，那么第一個zero point一定是在[3,4]這個區間之內的，選D選項。

通過這道題，大家也可以發現，如果我們找對了“路子”，兩分鐘之內我們就可以完成對這道題從切入到解決的所有過程，整個過程，我們都完全沒有想過這個函數到底有什么特性(domain/range/monotonicity/even or ood)等等。

我們也不需要知道它的exact value。這雖然給人一種“不求甚解”的假想，但AMC題目大多就像這道題一樣，最重要的就是要最快速的解決問題，有些時候太過于糾結數學題目的傳統解決方式，反而是某些大牛同學沒能取得好成績的原因。

以上就是AMC12題目的特點和解題思路了，當然僅僅了解這些還是不夠的，要想成功拿下AMC12還是要多做題多練習！

獲取備賽計劃，考前查缺補漏、重點沖刺

提前規劃2022年AMC系列賽事報名事項

掃碼即可【免費領取】相關真題及解析，還有不定期的高能講座等你來參加！