A-Level數學課程：復合函數如何求導

求導顧名思義，就是找到一個函數的導數 – 這樣做是為了找到這個函數的變化率。如果我們對函數 求導，我們會得到=(文末附帶的表格里有其它一些常見函數的導數)。我們也可以用符號 f'(x) 來表示一個函數f(x)的導數（其實就是在f(x)的f右上角加一撇）。

復合函數可以理解成‘函數的函數’ – 可以寫作? f(g(x))。

例如：? sin(2x) 就是由 f(x)=sin(x) 和 g(x)=2x按照上述方式得到的復合函數。f(x) 經常被叫做 “外層函數（可以理解成餃子皮）”，而 g(x) 叫“內層函數（理解成餃子餡，兩者在一起包成一個完整的“復合函數餃子”）”。

在A-Level Pure Mathematics 3第六章中，我們第一次接觸chain rule (鏈式法則)，它是微積分求導方法之一，用于復合函數的求導，公式為。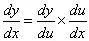

復合函數的導數將是構成復合這有限個函數在相應點的導數的乘積，就像鎖鏈一樣一環套一環，故稱鏈式法則。筆者對于2017-2020真題分析后，發現運用鏈式法則解題的考察頻率接近15%，無論出題頻率還是分值占比都非常高，所以考生們需要引起足夠重視。

A-Level數學課程：復合函數如何求導。首先，我們一起回顧一下在P1中所學習的導數運算。

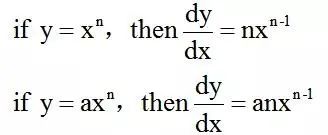
但是根據以往所學你會發現依然無法做出下面↓這道例題，那么很心酸7分就這么舍你而去了。原因何在呢？

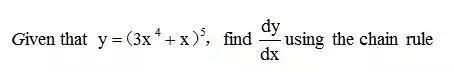
是因為這道題是針對復合函數進行求導，需要利用chain rule來進行解題。chain rule是針對復合函數的求導，所以應用該法則最根本還是掌握復合函數的分解。

那么接下來，我們就一起練習如何把復合函數分解成多個初等函數。

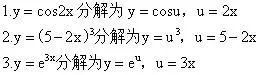
掌握了復合函數分解之后，現在我們就可以來學習如何利用三步法對于該函數進行求導了。示例：

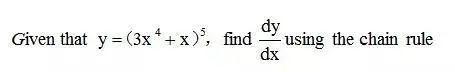
第三步一定不要忘記把x替換中間變量u的表達式。下圖即為復合函數求導三步法，大家一起來復習下。

最后歸納總結，chain rule就是對復合函數進行微分的方法。導數的知識點從P1到P4都有涉及，考察頻率之高大家需要精準掌握如何利用三步法chain rule對函數進行求導，才能取得理想好分數。

需要針對A-level考試輔導提升的同學 歡迎掃碼咨詢喔~

還能【免費領取】相關真題及解析！