全球頂尖數學夏校——羅斯數學訓練營（Ross）正式開放申請！申請流程+入營測試

眾所周知，對于想通過學術亮點進入前20名校的學生來說，能申請到一個非常具有含金量的項目，論證自己的學術能力非常重要，幾乎可以說“一只腳已經踏入了藤校”。近日，美國頂尖數學夏令營——Ross數學營正式開始招募！

經歷2020-2021疫情影響之后，美國頂尖數學夏令營——Ross數學營決定2022年取消線上營以及亞洲營地，轉而在美國開設兩個線下營地，每個營地招收60名新生。夏校課程大多都是以美國學校為基地，由本校的老師上課，擁有成熟固定的課程供大家選擇，涉及的內容包括ESL、科學、體育、藝術等等。

夏校之中分的種類也很多，首先是一切學科的基礎——數學夏校。

申請數學夏校的好處如下：

數學是理化生及經濟學的基礎學科，對于不確定未來專業方向的學生來講申請數學夏校是最穩妥最有效的背景提升方法；

ROSS、SUMaC、PROMYS等頂尖數學夏校含金量極高，錄取的國際學生少之又少，進入這些數學夏校意味著一條腿已經踏進了常青藤；

數學夏校一般不強制要求標化成績，對于數學優異卻沒有時間刷標化的同學們來講，更人性化。

羅斯數學訓練營The Ross Mathematics Program

項目課程

創辦時間：1957年
資方：圣母大學教授創辦、俄亥俄州立大學主辦、克雷數學研究所協辦
參與年級：15-18歲
項目所在地：分為美國營和亞洲營（2016年第一屆），美國營1964-2018舉辦地為俄亥俄州立大學，2019為俄亥俄多米尼加大學，2020-2021為線上項目
費用：$1500（2021年）

項目特點

和眾多美國大學為高中生開設的學分夏校（2-6周時長）不同，Ross不提供大學課程學分，也不計算課程成績和GPA。所有完成項目的學生，將會在項目結束時收到官方頒發的結業證書，表現優異的學生提供教授推薦信。

每周上課時間少。除了每周固定的5小時講座和3小時研討會，其余時間學生均用來完成課上未解決的數學題，學生可選擇獨立完成題目或和助教、同學討論。在解決每一個數學題后，學生必須提交一份清晰、完整的英文證明過程，鍛煉邏輯思維和撰寫嚴謹數學證明的能力。

Ross課程將會加深學生對數論 (Number Theory) 的理解和運用，為大學本科甚至研究生階段的數學學習打下堅實基礎。通過完成每個課程主題的數學題，學生將熟練掌握數論證明的過程：總結規律、提出假設、探索能證明假設的例子、總結數論、撰寫數論證明、完善數論、并探索數論的具體應用。

“簡單問題，深度思考”是羅斯訓練營的主要理念。

美國及其他世界名校數學教授傾情授課，課外輔導與討論相結合，通過具體的數論問題研究，旨在激發學員對數學學習的興趣，培養辯證思維能力。
營期全封閉管理學習，為數學愛好者提供難得的學習交流平臺。
具體的課程科目有：歐幾里得算法、模運算、二項式系數、多項式、元素的階、二次互反性、連分式、算術函數、高斯整數、有限域等。

申請材料

01必須提交

官網數學題解答 （一共4題，每題以手寫或LaTeX格式作答，需詳細描述解題思路和論證過程，以PDF格式提交）

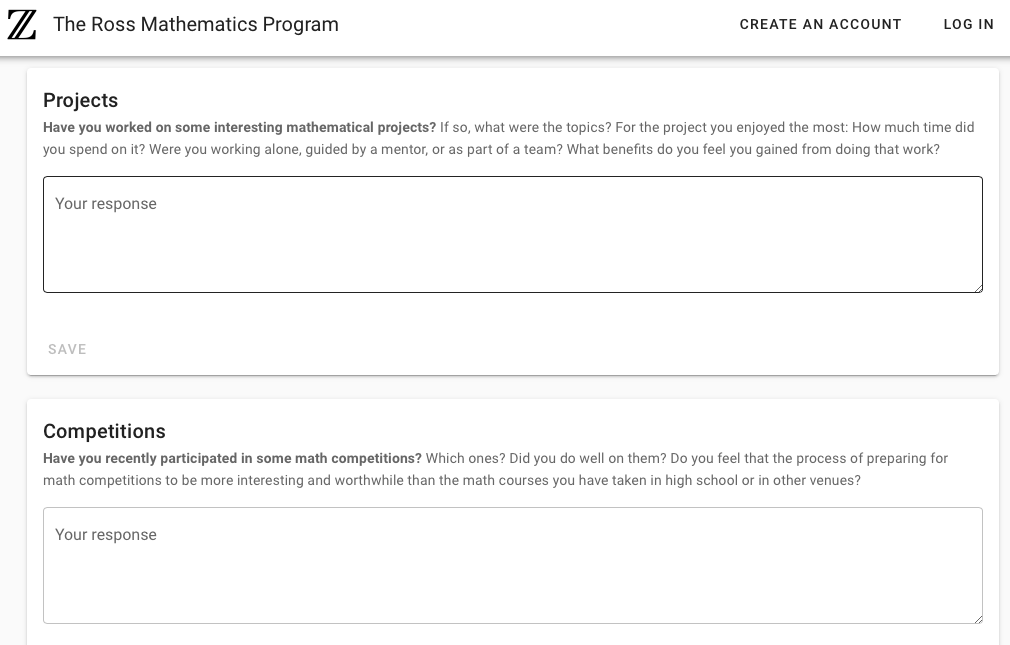
1篇個人陳述（字數不限），闡述學生對數學的興趣、成就和申請項目的原因

8篇簡短回答（字數不限）, 可參考：https://apply.rossprogram.org/apply/essays

高中官方成績單

1篇高中數學老師推薦信

英語能力證明（如托福、雅思成績）

02選擇提交

獎學金申請

簡歷（以強調數學方面的成就為主）

數學相關學術活動獎項

以下為Ross官網發布的2021年文書題目

以下為Ross官網發布的2021年數學題

2022Ross夏校申請題

Ross營申請材料中，申請題Solution是必須要提交的一項材料，隨著申請通道的開放，今年的入營試題也已經公布了↓

※申請題目一覽
The number systems Z and Zm (for a positive integer m) were defined in the previous
problem. We also use the notations:
Q is the system of rational numbers.
4Z is the set of multiples of 4 in Z. Similarly for 4Z12.
Consider the following number systems:
Z, Q, 4Z, Z3, Z8, Z9, 4Z12, Z13.
One system may be viewed as similar to another in several different ways.
(a) Let’s measure similarity using algebraic properties. First consider the following
sample properties:
(i) If a2 = 1, then a = ±1.
(ii) If 2x = 0, then x = 0.
(iii) If c2 = 0, then c = 0.
Which of the systems above have properties (i), (ii), and/or (iii)?
(b) Formulate another algebraic property and determine which of those systems have
that property.
Write down some additional algebraic properties and investigate them.
(c) In your opinion, which of the listed systems are “most similar” to each another?