Alevel數學—當證明題遇到函數題，怎么解？

Proof 證明題和 Function 函數題是Alevel數學考試中常見考點，官方數據中顯示，在二者結合的題型中，考生往往拿不到滿分，那我們如何在這類題型中拿到滿分呢？

今天要講的這道題，出現在2019年Alevel 數學Pure Math Paper 1試卷中，正是綜合了Proof和Function兩個考點的經典真題。雖然此題總共6分，初見并不覺得非常復雜，但令人驚訝的是，當年考生的平均得分只有29%！同學們比較擅長直接運用已經被證明好的結論，因而忽略了如何去證明結論的正確性，這一類的題型往往讓同學無法獲得滿分。

先來一起看看Alevel 數學P1這道題目：

下面，讓我們一題一題解：

Question 10(i):

在Part 1中，我們需要證明當時（N: Set of Natural Number/ 自然數），不能夠被4整除，由于題目中要求的是證明所有的n都需要滿足條件，所以這是一道需要Proof by Exhaustion的題型，因此我們不能直接代入數字舉例證明。

我們可以把n的取值分為even number （偶數）和odd number （奇數）：
?When n is even number, n = 2k, where k is an integer （2的倍數皆偶數）

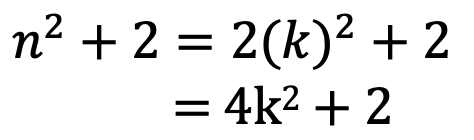
由此我們能得出，當n為偶數時，要比4的倍數多了2，所以不能被4整除
?When n is odd number, n = 2k + 1, where k is an integer（偶數的值加1為奇數）

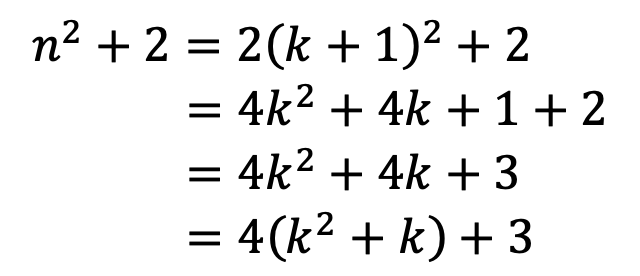
由此我們能得出，當n為奇數時，要比4的倍數多了3，所以同樣不能被4整除

綜上，我們能得出以下結論：當n為偶數和n為奇數的情況下，都不能被4整除。因此，當（任意自然數）時，都不能被4整除。

Question 10(ii):

Part 2雖然只是一道2分的題目，但是其實相對來說要比Part 1稍微復雜一些，我們的考試局經常喜歡出這種題型，需要同學們判斷題干中的Statement是否Always True(總是正確)，Sometimes True(有時候正確)，或者是Never True(錯誤)。

同學們可以暫停思考一下，如果判斷為Always True/ Never True，是一道什么類型的題型呢？
（接著往下看，就能找到答案哦~）

回到題干中提到的Statement，我們需要判斷當時，3x – 28的絕對值大于或者等于x - 9的正確性，如果判斷為Always True或者Never True，即相當于一道Proof （證明題），與我們Part 1的部分相類似。

第一步

我們可以把Statement文字描述轉換成數學的不等式，|3x–28|≥x–9，通過解出此不等式，找到這個Modulus Inequalities的x取值范圍，運用Algebraic Method去總結結論：

同學們要注意去掉絕對值符號時，我們需要分為兩種情況：

?當3x-28≥0時，解3x-28≥x-9
?當3x-28<0是，解-(3x-28)≥x-9

所以，不等式|3x–28|≥x–9的解是x≥9.5；x ≤9.25

第二步

我們嘗試代入在x≥9.5；x≤9.25區間范圍之內的值和區間范圍之外的值進行驗證：

綜上所述，我們可以得出以下結論:Hence, the statement is sometimes true.

最后我們也可以運用我們在GCSE/IGCSE中學過的知識點，分別畫出y = |3x – 28|和y =? x – 9的圖（如下圖所示），從而佐證在第二步中得到的結論，一部分的Modulus Graph是大于y = x – 9, 而另一部分是小于y = x – 9的。

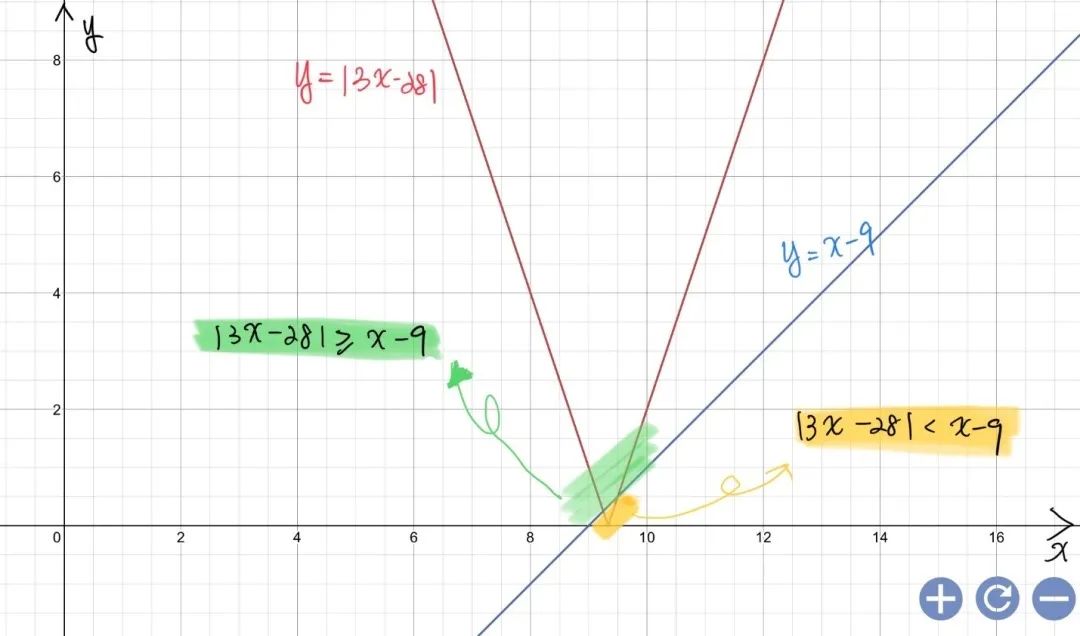
好啦，今天的Alevel數學P1干貨就分享到這里！大家有沒有學會呢？了解了這類Proof題型的解題方法以后，有沒有發現，證明題其實沒有想象的那么復雜呢？不要忘記動手實踐一遍，找一找相類似的題目，多練習一下吧！這樣才能更好的鞏固哦~