2021年澳大利亞數學思維挑戰活動5-6年級知識點匯總！

因國際教學模式多為螺旋式，所以相鄰等級測試所運用的知識點多為相近，變化主要體現在試題難易程度，對于知識的掌握理解運用。

此篇知識點主要針對B-Upper Primary ，小學五到六年級的學生

1、計算

一、乘、除法混合運算的本質

商不變性質：被除數和除數乘（或除）以同一個非零數，其商不變。

即：a÷b=(a×n)÷(b×n)=(a÷m)÷(b÷m)

m≠0,n≠0

在連除時，可以交換除數的位置，商不變。

即：a÷b÷c=a÷c÷b

除法運算律：a÷c±b÷c=(a±b)÷c

在乘、除混合運算中，被乘數、乘數或除數可以連同運算符號一起交換位置（即帶著符號搬家）。

例如：a×b÷c=a÷c×b=b÷c×a

在乘、除混合運算中，去掉或添加括號的規則。

去括號情形：

（1）?括號前是“×”時，去掉括號后，括號內的乘、除號不變。

即：a×(b×c)=a×b×ca×(b÷c)=a×b÷c

（2）?括號前是“÷”時，去括號后，括號內的“×”變成“÷”，“÷”變成“×”。

即：a÷(b×c)=a÷b÷ca÷(b÷c)=a÷b×c

添加括號情形：

（1）括號前是“×”時，

加括號時，括號內的乘、除號不變。

即：a×b×c=a×(b×c)a×b÷c=a×(b÷c)

（2）括號前是“÷”時，

加括號時，括號內的“×”變成“÷”，“÷”變成“×”。

即：a÷b÷c=a÷(b×c)a÷b×c=a÷(b÷c)

兩個數之積除以兩個數之積，可以分別相除后再相乘。

即：(a×b)÷(c×d)=

(a÷c)×(b÷d)=(a÷d)×(b÷c)

二、常用特殊數的乘積

125×8＝1000?25×4＝100?125×3＝375

625×16＝10000?7×11×13＝1001

25×8＝200?125×4＝500?37×3=111

三、其它特殊數的乘積

拉面數（乘“11”），

例如：11×11=121;

89×11=979;

2014×11=22154;

重碼數，

例如：201620162016=2016×1001001

山頂數，

例如：

12345678987654321=111111111×111111111

（“1”的個數最大為?9）

輪轉數，

例如：1234+2341+3412+4123=(1+2+3+4)×1111

走馬燈數：

142857×1=142857;

142857×2=285714;

142857×3=428571;

142857×4=571428;

142857×5=714285;

142857×6=857142;

142857×7=999999。

缺八數：12345679×9=111111111

四、相關公式

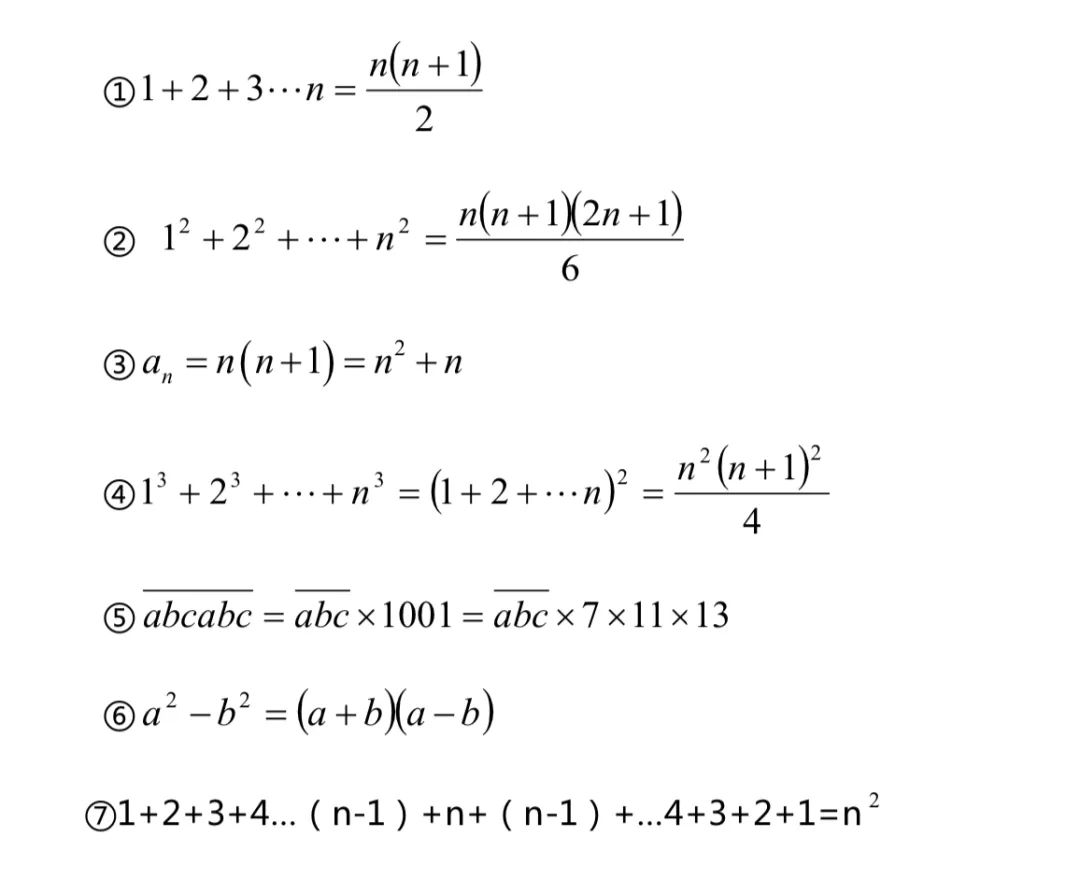
五、數字謎問題

1、一般是指那些含有未知數字或未知運算符號的算式。

這種不完整的算式，就像謎一樣，要解開這樣的謎，就得根據有關的運算法則、數的性質（和差積商的位數，數的整除性、奇偶性、位數規律等）來進行正確的推理、判斷。

2、解數字謎

一般是從某個數的首位或末位數字上尋找突破口。推理時應注意：

1. 數字謎中的文字、字母或其它符號，只取?0-9 中的某個數字；

2. 要認真分析算式中所包含的數量關系，找出盡可能多的隱蔽條件；

3. 必要時應采用枚舉和篩選相結合的方法（試驗法），逐步淘汰掉那些不符合題意的數字；

4. 數字謎解出之后，最好驗算一遍。

2、幾何

一、?圖形剪拼

即幾何操作題，包括：

1、?等分面積；

2、 等分三角形；

3、 分割與拼合；

4、 多邊形分割；

注：平面圖形分割前后總面積不變。

經典三步：算、切、拼。

二、還原問題

方法：箭頭表示法

注意：倒推時，加減互逆，乘除互逆。

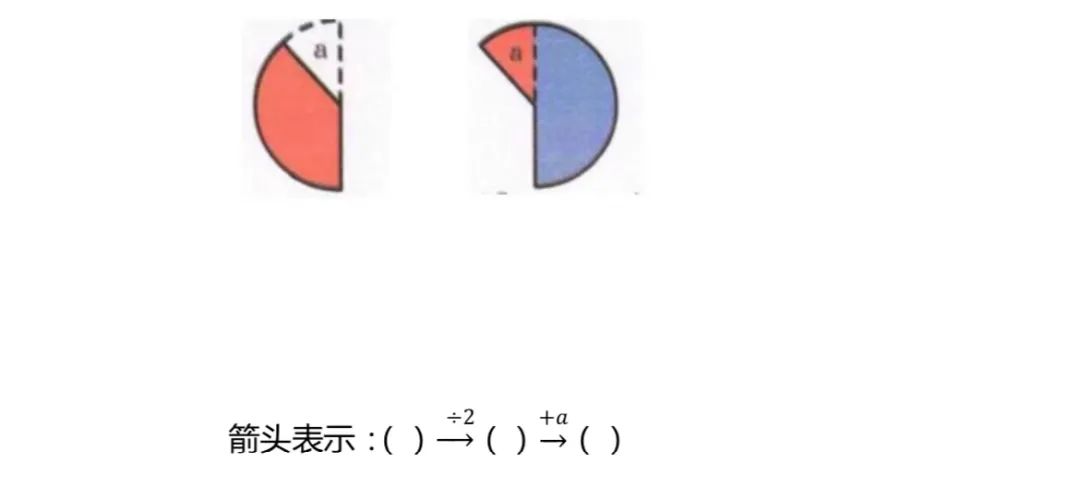
3.?多者還原問題

多組箭頭表示（注意：步調一致）

4.?算式出錯型

①加法：加數增大?和增大

②減法：被減數增大?差增大

減數增大?差減少

③乘法

④除法

三、對稱軸問題

①線段有兩條對稱軸，是這條線段的垂直平分線和線段所在的直線。

②角有一條對稱軸，是角平分線所在的直線。

③等腰三角形有一條對稱軸，是頂角平分線所在的直線。

④等邊三角形有三條對稱軸，分別是三個頂角平分線所在的直線。

⑤矩形有兩條對稱軸，是相鄰兩邊的垂直平分線。

⑥正方形有四條對稱軸，是相鄰兩邊的垂直平分線和對角線所在的直線。

⑦菱形有兩條對稱軸，是對角線所在的直線。

⑧等腰梯形有一條對稱軸，是兩底垂直平分線。

⑨正多邊形有與邊數相同條的對稱軸。

⑩圓有無數條對稱軸，是任何一條直徑所在的直線

四、幾何面積知識點

1、基本思路：

在一些面積的計算上，不能直接運用公式的情況下，一般需要對圖形進行割補，平移、旋轉、翻折、分解、變形、重疊等，使不規則的圖形變為規則的圖形進行計算;另外需要掌握和記憶一些常規的面積規律。

2、常用方法：

a.?連輔助線方法

b. 利用等底等高的兩個三角形面積相等。

c. 大膽假設(有些點的設置題目中說的是任意點，解題時可把任意點設置在特殊位置上)。

d.?利用特殊規律

①等腰直角三角形，已知任意一條邊都可求出面積。(斜邊的平方除以 4 等于等腰直角三角形的面積)

②梯形對角線連線后，兩腰部分面積相等。

③圓的面積占外接正方形面積的 78.5%。

3、基礎公式

1）長方形的周長=(長+寬)×2C=(a+b)×2

2）正方形的周長=邊長×4C=4a

3）長方形的面積=長×寬?S=ab

4）正方形的面積=邊長×邊長?S=a*a=a2

5）三角形的面積=底×高÷2S=ah÷2

6）平行四邊形的面積=底×高?S=ah

7）梯形的面積=(上底+下底)×高÷2S=(a+b)h÷2

8）直徑=半徑×2d=2r?半徑=直徑÷2r=d÷2

9）?圓的周長=

圓周率×直徑=圓周率×半徑×2c=πd=2πr

10）圓的面積=圓周率×半徑×半徑

五、幾何體

立體圖形相關公式

依次為：名稱、圖形特征、表面積、體積

長方體;

8 個頂點，6 個面，相對的面相等，

12 條棱，相對的棱相等;

S=2(ab+ah+bh)

V=abh=Sh

正方體;

8 個頂點;6 個面，所有面相等，

12 條棱，所有棱相等;

S=6a2

V=a3

圓柱體;

上下兩底是平行且相等的圓，側面展開后是長方形;

S=S 側+2S 底

S 側=Ch V=Sh

圓錐體;

下底是圓，只有一個頂點，

l：母線，頂點到底圓周上任意一點的距離;

S=S 側+S 底

S 側=rl V=Sh

球體;

圓心到圓周上任意一點的距離是球的半徑。

S=4r2

3、數論

一、整除初步

1、若整數?a?除以非零整數?b，商為整數，且余數為零，我們就說 a 能被 b 整除（或說 b 能整除 a），記 b|a，讀作“b 整除 a”或“a 能被 b 整除”。

2、能被 2、3、5、9 整除數的特征

1）.能被 2 整除的數的特征：個位上是 0、2、4、6、8 的數都能被 2 整除。

（1）?能被 2 整除數叫做偶數；不能被 2 整除的數叫做奇數。

（2）?奇數±奇數=偶數；偶數±偶數=偶數；

（3）?奇數±偶數=奇數；偶數±奇數=奇數。

（4）?多個數相加（減）時，奇數個奇數之和（差）還是奇數。

2）.能被 3 整除數的特征：一個數的各個數位上的數字的和能被 3 整除，這個數就能被 3 整除。

被 3 整除數的特征的位值原理證明：

假設一個任意的四位數ˉaˉbˉcˉdˉ，它可以表示為：

ˉaˉbˉcˉdˉ?=?1000a?+?100b+?10c+?d

= 999a + a + 99b + b + 9c + c +?d

= 999a + 99b + 9c + a + b + c +?d

= (999a + 99b + 9c) + (a + b + c + d).

因為 3|999a+99b+9c，所以只要 3| a+b+c+d 即可，即上述定義。

注：能被 3 整除的數還可以用“棄 3 法”進行判斷：如果該數中有 3 或者 3 的倍數的數全部棄掉，最后如果所有的數字能全部棄掉，則該數可以被 3 整除。

3）.能被 5 整除數的特征：個位上是 0 或 5 的數都能被 5 整除。

能被 5 整除數的特征的位值原理證明：

假設一個任意的四位數ˉaˉbˉcˉdˉ，

它可以表示為：ˉaˉbˉcˉdˉ=1000a+100b+10c+d

因為?5|1000a+100b+10c，所以只要5|d?就可以了，即上述定義。

4.）能被 9 整除數的特征：一個數的各個數位上的數字的和能被 9 整除，這個數就能被 9整除。

被 9 整除數的特征的位值原理證明：

假設一個任意的四位數ˉaˉbˉcˉdˉ，它可以表示為：

ˉaˉbˉcˉdˉ?=?1000a?+?100b+?10c+?d

= 999a + a + 99b + b + 9c + c +?d

= 999a + 99b + 9c + a + b + c +?d

= (999a + 99b + 9c) + (a + b + c + d).

因為 9|999a+99b+9c，所以只要 9| a+b+c+d 即可，即上述定義。

注：能被 9 整除的數還可以用“棄 9 法”進行判斷：如果該數中有 9 或者 9 的倍數的數全部棄掉，最后如果所有的數字能全部棄掉，則該數可以被 9 整除。

3、2、3、5 整除的綜合應用

1. 能同時被 2、5 整除的數的特征：個位上必須是?0.

2. 能同時被 2、3 整除的數的特征：偶數，且數字和是 3 的倍數。

3. 能同時被 3、5 整除的數的特征：個位為?0?或 5，且數字和是 3 的倍數。

4. 能同時被 2、3、5 整除的數的特征：首先個位上必須是?0，其次這個數的各個數位上的數字的和能被 3 整除。

二、“奇偶分析法”

常用知識：

1、奇數表示：2n+1 或 2n-1

2、偶數表示：2n

3、加減法（加減同性）：

偶數+偶數=偶數；奇數+奇數=偶數；偶數+奇數=奇數；

4、乘除法：

偶數×奇數=偶數

（推廣開來還可以得到：偶數個奇數相加得偶數）

偶數×偶數=偶數

（推廣開就是：偶數個偶數相加得偶數）

奇數×奇數=奇數

（推廣開就是：奇數個奇數相加得奇數）

5、任何一個奇數一定不等于任何一個偶數。

三、至多至少問題

至少：就是取滿足條件中所有數的最小值.這句話有兩個意思,第一,在指定集合范圍內,必須都滿足要求,第二,指定集合存在最小值.

例如,已經-x2≤a 在所有實數都成立,那么 a 的最小值是多少.

第一,先求出滿足-x2≤a 所有 a 的值,顯然只要 a≥0,

第二,a=0 是這個集合的最小值,所以 a 的最小值是 0. 兩個條件之中有一個不滿足,就沒有最小值。

至多：就是取滿足條件中所有數的最大值.

這句話也有兩個意思,第一,在指定集合范圍內,必須都滿足要求,第二,指定集合存在最大值.

四、同余定理

①同余定義：若兩個整數 a，b 被自然數 m 除有相同的余數，那么稱 a，b 對于模 m 同余，?用式子表示為a≡b(mod m)

②若兩個數 a，b 除以同一個數 c 得到的余數相同，則 a，b 的差一定能被 c 整除。

③兩數的和除以 m 的余數等于這兩個數分別除以 m 的余數和。

④兩數的差除以 m 的余數等于這兩個數分別除以 m 的余數差。

⑤兩數的積除以 m 的余數等于這兩個數分別除以 m 的余數積。

五、100 內質數

2 3 5 7 11 13 17 19 23 29 31 37 41

43 47 53 59 61 67 71 73 79 83 89 97

4、組合初步

一、解排列組合問題

首先要弄清一件事是"分類"還是"分步"完成,對于元素之間的關系,還要考慮"是有序"的還是"無序的",也就是會正確使用分類計數原理和分步計數原理,排列定義和組合定義,其次,對一些復雜的帶有附加條件的問題,需掌握以下幾種常用的解題方法:

1、特殊優先法

對于存在特殊元素或者特殊位置的排列組合問題,我們可以從這些特殊的東西入手,先解決特殊元素或特殊位置,再去解決其它元素或位置,這種解法叫做特殊優先法.

例如:用 0,1,2,3,4 這5個數字,組成沒有重復數字的三位數,其中偶數共有 ?-___個.(答案:30個)

2、科學分類法

對于較復雜的排列組合問題,由于情況繁多,因此要對各種不同情況,進行科學分類,以便有條不紊地進行解答,避免重復或遺漏現象發生

例如:從 6 臺原裝計算機和 5 臺組裝計算機中任取5?臺,其中至少有原裝與組裝計算機各兩臺,則不同的選取法有___種.(答案:350)

3、插空法

解決一些不相鄰問題時,可以先排一些元素然后插入其余元素,使問題得以解決

例如:7 人站成一行,如果甲乙兩人不相鄰,則不同排法種數是___.(答案:3600)

捆綁法相鄰元素的排列,可以采用"整體到局部"的排法,即將相鄰的元素當成"一個"元素進行排列,然后再局部排列

例如:6?名同學坐成一排,其中甲,乙必須坐在一起的不同坐法是___種.(答案:240)

4、排除法?

從總體中排除不符合條件的方法數,這是一種間接解題的方法.

二、其他解題方法

1、分類加法計數原理

完成一件事，有 n 類辦法，在第 1 類辦法中有 m1 種不同的方法，在第 2 類辦法中有 m2 種不同的方法‥‥‥則總共有 m1+m2+…+mn 種方法。

2、枚舉法

在進行歸納推理時，如果逐個考察了某類事件的所有可能情況，因而得出一般結論，那么這結論是可靠的，這種歸納方法叫做枚舉法。

采用枚舉算法解題的基本思路：

（1）確定枚舉對象、枚舉范圍和判定條件；

（2）枚舉可能的解，驗證是否是問題的解。

三、解題原理

1、加法原理：分類枚舉

2、乘法原理：排列組合

3、容斥原理：

總數量=A+B+C-(AB+AC+BC)+ABC

常用：總數量=A+B-AB

5、單位換算

1?米=3?尺=3.2808?英尺=1.0926?碼

1?公里=1000?米=2?里

1?碼=3?英尺=36?英?寸

1?海里=1852?米=3.704?里=1.15?英里

1?平方公里=1000000?平方米=100?公頃?=4?平方里=0.3861?平方英里

1?平方米=100?平方分米=10000?平方厘米

1?公頃=100?公畝=15?畝=2.4711?英畝

1?立方米=1000?立方分米=1000000?立方厘米

1 立方米=27 立方尺=1.308 立方碼=35.3147 立方英尺

1?噸=1000 公斤=1000?千?克

1?公斤=1000?克=2?斤（市制）=2.2046 磅