AP微積分丨敲黑板，這些知識點很重要

AP微積分

AP是The Advanced Placement Program的縮寫，即大學預修課程，指由college board提供的在高中授課的大學課程。由于美國大學把學生在AP考試中的表現作為衡量其是否能夠勝任大學學習的依據之一，選修AP課程和通過AP考試不僅是對學生能力和學業水平的證明，而且會令學生在申請大學時具有很大的優勢，尤其體現在頂尖大學的申請中。

進入大學后，又可以免修同類課程(各學校有轉換學時的具體規定)，提早選修更高級的課程，節省學費的同時提早畢業。在頂尖大學，4分以上或者5分可以換取相應學時；在前50的大學，4分就可以換取相應學時。AP微積分是歷年AP考試中報考人數最多的一門課程，其知識深度和知識結構相當于美國大學一年級的微積分課程，是所有AP科目中語言對其影響最小的課程，也是5分率比較高的科目。

在諸多大學熱門專業中，如金融學、計算機科學、生命科學、社會學及工程學等，微積分都是必修課程。AP微積分分為AB 和BC兩門課程，BC的內容和難度都高于AB的考試，AB 的內容大概占BC內容的70%。鑒于微積分在大學教育中的重要地位，建議數學基礎較好的或準備申請理工類的學生考BC，非理工類的學生如果數學基礎一般就可報考AB。

AP微積分BC學習的核心內容是函數的極限、導數、積分和無窮級數四部分。其中，導數和積分是重點，無窮級數是難點。AB與BC比較而言，不涉及無窮級數、參數方程、極坐標方程、曲線運動以及部分不定積分的計算方法。試題則主要考察知識的理解、基本運算技能以及概念的基本應用。考試分為兩部分：選擇題和問答題。具體分配如下：

考試中使用的計算器必須具備以下功能：·在任意大小的窗口畫函數圖像·找函數零點（數值求解方程）

·計算函數在某一點的導數

·計算函數的積分值
?
在完成第二部分Free Response題目時，需要注意以下問題：

·方法和答案的正確性及完整性。沒有給出數學依據的答案是得不到相應分數的。

·解題過程中要使用標準數學符號，而不是計算器語言。

·除非另有說明，答案（數字或代數）不需要簡化，小數應精確到小數點后三位。

·除非另有說明，函數的定義域被假定為所有實數的集合。
?
一般情況，AP微積分考試正確率在65%以上可確保5分。每年AP微積分的5分線會有小幅波動，但最高也沒有超過70分（滿分108分）。從2017年全球和中國考生的成績來看，雖然BC比AB的學習內容要多，但BC的5分率要高出不少。因此，對于數學基礎較好的學生，推薦大家選擇BC。
?2017年AP微積分考試得分情況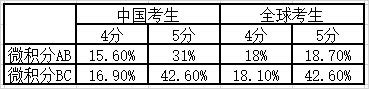

AP微積分考點總結

A. 函數

(1) 函數的定義和性質(定義域值域、單調性、奇偶性和周期性等)

(2) 五種基本初等函數(冪函數、指數、對數、三角和反三角函數的運算公式和函數性質及圖像)

(3) 復合函數，反函數

(4) 函數圖像平移和變換
*(5) 參數函數，極坐標函數，分段函數

B. 極限和連續

(1) 極限的定義和左右極限

(2) 極限的運算法則和有理函數求極限

(3) 兩個重要的極限

(4) 極限的應用-求函數漸近線

(5) 連續的定義

(6) 三類不連續點(移點、跳點和無窮點)

(7) 最值定理、介值定理和零值定理

C. 導數

(1) 導數的定義、幾何意義和單側導數

(2) 極限、連續和可導的關系

(3) 導數的求導法則

(4) 復合函數、反函數、隱函數的求導

(5) 高階導數

*(6) 參數函數求導數和極坐標求導數

D. 導數的應用

(1) 幾何應用-切線和法線和相對變化率

(2) 物理應用-求速度和加速度(一維和二維運動)

(3) 微分中值定理

(4) 求極值、最值，函數的增減性和凹凸性

(5) 洛比達法則求極限

(6) 微分定義及線性估計

(7) 歐拉法則求近似值

E. 不定積分

(1) 不定積分和導數的關系

(2) 不定積分的公式

(3) U換元法求不定積分

*(4) 分部積分法求不定積分

*(5) 分式拆分求不定積分

F. 定積分

(1) 黎曼和的極限及定積分的定義與幾何意義

(2) 定積分的性質

*(3) 累計函數求導數

*(4) 反常函數求積分

G. 定積分的應用

(1) 積分中值定理

(2) 定積分求面積、體積

(3) 曲線長度

(4) 定積分的物理應用

H. 微分方程

(1) 可分離變量的微分方程和邏輯斯特微分方程

(2) 斜率場

*I. 無窮級數

(1) 無窮級數的定義和數列的級數

(2) 三種審斂法：比值、積分和比較審斂法

(3) 四種級數：調和級數、幾何級數、P級數和交錯級數

(4) 冪級數(收斂半徑)、泰勒級數和麥克勞林級數

(5) 級數的運算和拉格朗日誤差（限）