AP Statistics | Unit 6 Random Variable (下)

大家好呀今天我們來看Random Variable單元的下半部分（以及被催稿之下的人們的腦回路是怎樣的)

這次的內容摘要-Binomial Random Variables-Binomial Distribution-Binomial Formula-Mean and standard deviation-Geometric Random Variables-Geometric Distribution-Mean of geometric distribution

-Normal Conditions

Binomial Setting二項隨機變數的特點其實可以概括成“BINS”，也就是Binary：只有兩種結果（outcome）——就是success和failure

Independent：是獨立事件，trial和trial之間的結果不能互相影響。

Number of Trials：trials的次數一定是固定的。注意，這個是binomial和geometric的主要區別之一！

S(success)：success的幾率(probability)

Binomial event的舉例：

現在我有一大袋彩虹糖，想知道里面有多少黃色的，于是我打算總共從里面SRS二十顆(fixed number of trials)，with replacement，分為是黃色(success)和不是黃色 (failure)兩種結果。最后，二十顆里有10顆是黃色，于是success(S)的幾率就是0.5。

接著，我重復這個過程很多很多次，每次的結果都記錄在一個graph上，就變成了這個事件的Binomial Distribution，可以表示為Bin (n, p)，n為number of trials，p是success的幾率。

再來，就是比較重點的計算部分了，值得開心的是，統計的計算看似復雜，但是在計算器的幫助下根本不算個事兒：這里就直接舉例子了！

擲篩子5次，求得到一次數字4的幾率是多少：

這時候可以再TI-Nspire里輸入binopdf(5, 1/6, 1)，這三個數字分別代表剛才提到過的n，p，而1便是出現這個結果的次數。

而用這種方法直接算得到的結果也是一樣的，可以說會更直觀：(見圖)

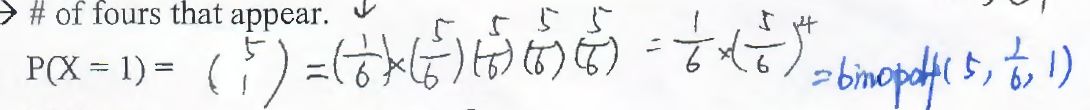還有，Check you FORMULA SHEET!!!

遇到題的時候你才會發現formula sheet到底多么值得珍惜。

Mean and Standard Deviation?不哆說啊，直接套公式：?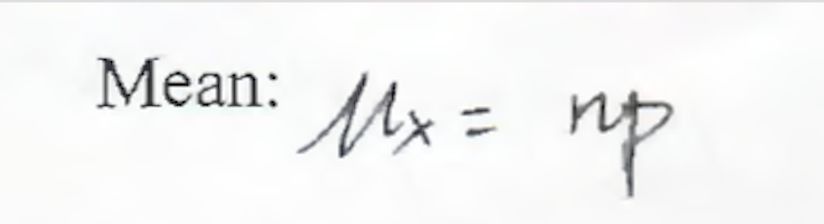

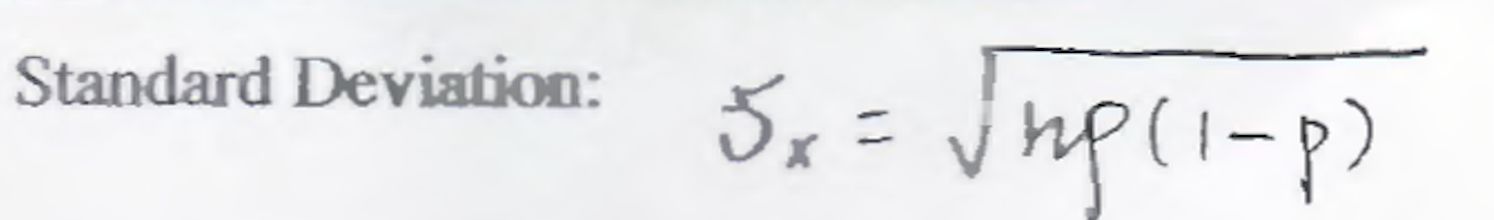
Geometric Setting ?Geometric Distribution跟BINS不一樣，geometric setting是BITS：

Binary一樣：只有success或failure兩種結果

Independent一樣：是獨立事件，trial和trial之間的結果不能互相影響。

Trials: 很不一樣！你只需要一直重復，直到出現第一次success就可以了。可以把geometric理解成累計的感覺。與Binomial的其他不同點-用p表示，沒有固定的n(number of trials)

-跟binomial distribution不一樣，不包括0次，因為至少要有1次才能出現success的情況。
-always skewed to the right（大部分聚集在左邊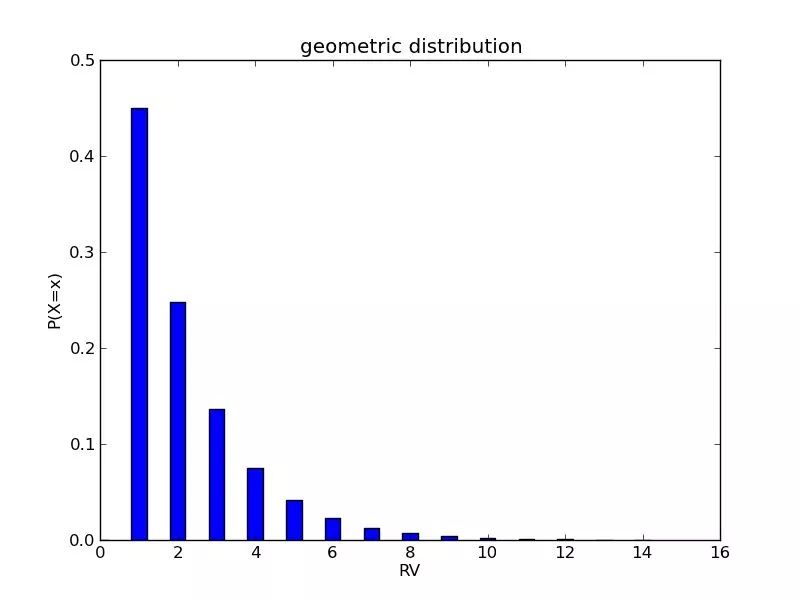） ?Mean of geometric Distribution ?p的倒數，也就是1/p。

Normal Conditions最后，既然geometric distribution是skewed right，那么binomial呢？是normal嗎？

不一定。上述binomial的那兩條formula，其實是要在試驗次數夠大的時候才能用的，不然結果會很不準確進而產生bias。那何時才能用此神技？

如果np>10, 并且n(1-p)>10，

你就可以用normal approximation了，也就是直接假設這個distribution是normal的。?那么,到此為止，

AP Statistics的內容你已經學了一半了

對5月份的考試有信心嗎？

一般，沒有才是正常的，

所以繼續努力吧

紙質版筆記的鏈接：

https://pan.baidu.com/s/1cEtvVS? 密碼：gpqz