- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
ICM實用模型及例題(E題)
2018/1/17周三國內常說的美國大學生數學建模學術活動,其實是由兩種類型的學術活動組成,MCM即Mathematical Contest in Modeling,
直譯為數學建模學術活動,和ICM即The Interdisciplinary Contest in Modeling,直譯為交叉學科建模學術活動,兩者名稱不同,題目的風格有較大的差異。
ICM學術活動題目更開放,問題更“大”,更宏觀,篇幅較長,往往是全球范圍內共同關心的問題,因此一般不依賴特定的文化背景或生活習慣,近幾年ICM學術活動要求論文正文部分不超過20頁。
E題:environmental science
問題簡介E題是環境科學問題,大體上會集中在環境污染、資源短缺、可持續發展、生態保護等幾個方面。
環境與可持續發展是當今世界關注的重要議題,可持續發展的關鍵是協調好經濟發展和環境保護之間的關系,這種協調有賴于應用系統論的觀點研究環境系統內部各個組成部分和要素之間的對立統一關系;
也有賴于研究環境質量和社會經濟發展的對立統一關系,建立最佳的經濟結構和環境—經濟布局,環境科學的發展給日益顯現和加劇的環境問題的解決提供了重要方法和技術。
科學計算和數學模型的研究在環境科學研究和工作實踐中占有重要地位,它是環境科學與其所依托的傳統學科之間進一步交叉互動發展的需要,是量化認識、準確調控復雜環境系統的需要,也是環境科學研究的重要工具、環境規劃、環境評價的核心技術之一。
今天我們主要介紹Entropy熵值法、AHP層次分析法和PCA主成分分析法三種方法。
Entropy 熵值法熵,英文為entropy,是德國物理學家克勞修斯在1850年創造的一個術語,它用來表示一種能量在空間中分布的均勻程度。
熵是熱力學的一個物理概念,是體系混亂度(或無序度)的量度,用S表示。應用在系統論中,熵越大說明系統越混亂,攜帶的信息越少,熵越小說明系統越有序,攜帶的信息越多。
根據熵的特性,我們可以用熵值來判斷某個指標的離散程度:指標熵值越小,離散程度越大,該指標對綜合評價的影響(即權重)也就越大。
主要流程
Step1,確立指標體系
我們用手游認知客戶挖掘模型實例來解說熵值法計算指標權重的全過程。下圖是手游認知客戶挖掘模型的二級指標評價體系,其中各個維度指標對應的權重系數均是通過熵值法計算出來的。
下面具體看下模型中 “手游認知能力”部分指標權重的計算過程。 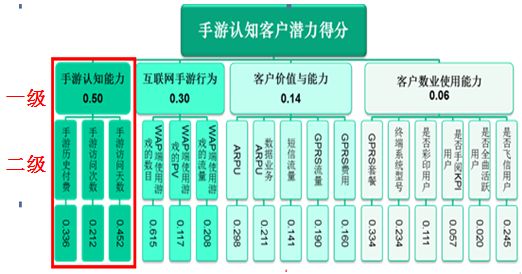
Step2,清洗指標極值方法:
即剔除各指標中極大或者極小的值,一般用比較合理的上下限值替換這些極值。目的是減少極值數據對該指標的熵的影響;
原則:剔除占樣本總數不到1-2%但指標值貢獻率超過20-30%以上的極值樣本 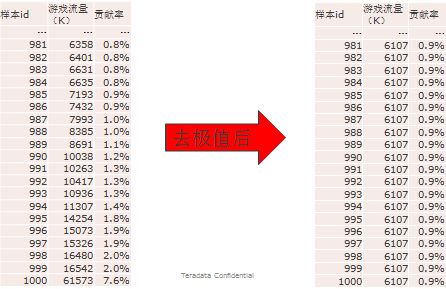 Step3,歸一化指標處理方法:
Step3,歸一化指標處理方法:
指標歸一化過程也稱之為指標的無量綱化,即將指標實際值轉化為不受量綱影響的指標平價值。方法比較多,具體見附錄《無綱量化方法一覽》;
原則:比較常用的是臨界值法和Z-score法(更合理,保持了數據的連續性,減少數據信息丟失),最終將所有指標轉化為正區間里面,二者具體處理如下:  Step4,計算指標“熵”和“權”
Step4,計算指標“熵”和“權” 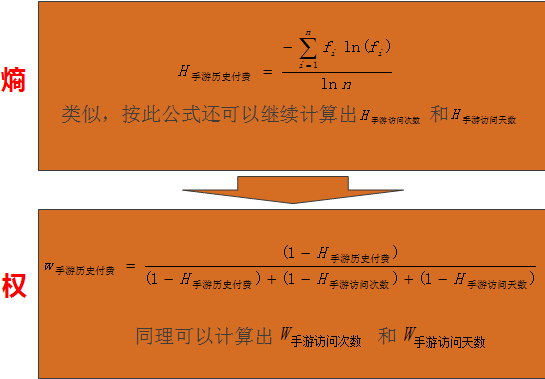
Step5,指標加權計算得分方法:
計算綜合得分就是指標合成的過程,一般可以采用加法原理和乘法原理;
原則:最常用的是加法合成法,其具體處理如下:
利用以上3個指標的權重和歸一化指標值,計算上級指標的分數:手游認知能力得分= 0.336*手游歷史付費金額+0.212*手游訪問次數 +0.452*手游訪問天數。
當然,模型其他部分的底層指標權重和一級指標權重均可以按以上步驟計算得到,并一層層由下往上進行加權,最終得到模型的綜合得分。
“AHP層次分析法層次分析法(AHP)是美國運籌學家匹茨堡大學教授薩蒂(T.L.Saaty)于上世紀70年代初,為美國國防部研究“根據各個工業部門對國家福利的貢獻大小而進行電力分配”課題時,應用網絡系統理論和多目標綜合評價方法,提出的一種層次權重決策分析方法。
這種方法的特點是在對復雜的決策問題的本質、影響因素及其內在關系等進行深入分析的基礎上,利用較少的定量信息使決策的思維過程數學化,從而為多目標、多準則或無結構特性的復雜決策問題提供簡便的決策方法。層次
劃分
最高層:決策的目的、要解決的問題
最低層:決策時的備選方案
中間層:考慮的因素、決策的準則
對于相鄰的兩層,稱高層為目標層,低層為因素層
主要流程
建立層次結構模型
例如,假期旅游,是去風光秀麗的蘇州,還是去涼爽宜人的北戴河,或者是去山水甲天下的桂林?通常會依據景色、費用、食宿條件、旅途等因素選擇去哪個地方。 如何在3個目的地中按照景色、費用、居住條件等因素選擇.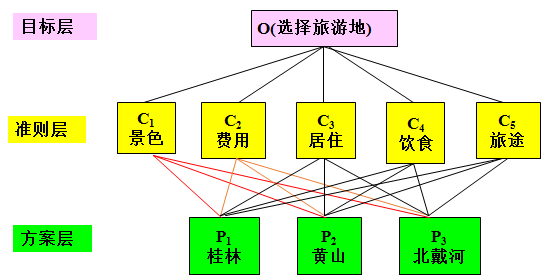 構造判斷(成對比較)矩陣在建立遞階層次結構以后,上下層次之間元素的隸屬關系就被確定了。假定上一層次的元素Ck作為準則,對下一層次的元素 A1, …, An 有支配關系,我們的目的是在準則 Ck 之下按它們相對重要性賦予 A1, …, An 相應的權重。比較同一層次中每個因素關于上一層次的同一個因素的相對重要性。
構造判斷(成對比較)矩陣在建立遞階層次結構以后,上下層次之間元素的隸屬關系就被確定了。假定上一層次的元素Ck作為準則,對下一層次的元素 A1, …, An 有支配關系,我們的目的是在準則 Ck 之下按它們相對重要性賦予 A1, …, An 相應的權重。比較同一層次中每個因素關于上一層次的同一個因素的相對重要性。
層次單排序及其一致性檢驗
一般地,我們并不要求判斷具有這種傳遞性和一致性,這是由客觀事物的復雜性與人的認識的多樣性所決定的。
但在構造兩兩判斷矩陣時,要求判斷大體上的一致是應該的。出現甲比乙極端重要,乙比丙極端重要,而丙又比甲極端重要的判斷,一般是違反常識的。
一個混亂的經不起推敲的判斷矩陣有可能導致決策的失誤,而且當判斷矩陣過于偏離一致性時,用上述各種方法計算的排序權重作為決策依據,其可靠程度也值得懷疑。因而必須對判斷矩陣的一致性進行檢驗。
定義一致性指標:![]() 有完全的一致性;CI接近于0,有滿意的一致性;CI 越大,不一致越嚴重。
有完全的一致性;CI接近于0,有滿意的一致性;CI 越大,不一致越嚴重。
定義一致性比率 :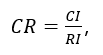 當CR<0.1時認為成對比矩陣的不一致程度在容許范圍之內,有滿意的一致性,通過一致性檢驗。層次總排序及其一致性檢驗
當CR<0.1時認為成對比矩陣的不一致程度在容許范圍之內,有滿意的一致性,通過一致性檢驗。層次總排序及其一致性檢驗
層次總排序的一致性比率:![]() 當CR<0.1時,認為層次總排序通過一致性檢驗。
當CR<0.1時,認為層次總排序通過一致性檢驗。
層次總排序具有滿意的一致性,否則需要重新調整那些一致性比率高的判斷矩陣的元素取值。“PCA主成分分析法主成分分析是把各變量之間互相關聯的復雜關系進行簡化的分析方法。
在社會經濟的研究中,為了全面系統的分析和研究問題,必須考慮許多經濟指標,這些指標能從不同的側面反映我們所研究的對象的特征,但在某種程度上存在信息的重疊,具有一定的相關性。
主成分分析試圖在力保數據信息丟失最少的原則下,對這種多變量的截面數據表進行最佳綜合簡化,也就是說,對高維變量空間進行降維處理。
主要流程
對原始數據進行標準化
計算相關系數矩陣
計算特征值與特征向量
計算主成分載荷
各主成分的得分
幾何解釋
假設我們所討論的實際問題中,有p個指標,我們把這p個指標看作p個變量,記為X1,X2,…,Xp,主成分分析就是要把這p個指標的問題,轉變為討論p個指標的線性組合的問題,而這些新的指標F1,F2,…,Fk(k≤p),按照保留主要信息量的原則充分反映原指標的信息,并且相互獨立。 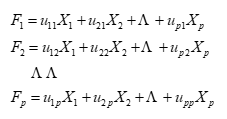

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









