Home » 國際競賽 » 數學國際競賽 » AMC美國數學競賽 » Details

1995AIME 真題及答案解析

Category: AMC美國數學競賽, 國際競賽 Date: 2019年12月12日上午10:54

1995AIME 真題及答案解析

答案解析請參考文末

Problem 1

Square? $S_{1}$ ?is? $1times 1.$ ?For? $ige 1,$ ?the lengths of the sides of square? $S_{i+1}$ ?are half the lengths of the sides of square? $S_{i},$ ?two adjacent sides of square? $S_{i}$ ?are perpendicular bisectors of two adjacent sides of square? $S_{i+1},$ ?and the other two sides of square? $S_{i+1},$ ?are the perpendicular bisectors of two adjacent sides of square? $S_{i+2}.$ ?The total area enclosed by at least one of? $S_{1}, S_{2}, S_{3}, S_{4}, S_{5}$ ?can be written in the form? $m/n,$ ?where? $m$ ?and? $n$ ?are relatively prime positive integers. Find? $m-n.$

Problem 2

Find the last three digits of the product of the positive roots of? $sqrt{1995}x^{log_{1995}x}=x^2.$

Problem 3

Starting at? $(0,0),$ ?an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let? $p$ ?be the probability that the object reaches? $(2,2)$ ?in six or fewer steps. Given that? $p$ ?can be written in the form? $m/n,$ ?where? $m$ ?and? $n$ ?are relatively prime positive integers, find? $m+n.$

Problem 4

Circles of radius? $3$ ?and? $6$ ?are externally tangent to each other and are internally tangent to a circle of radius? $9$ . The circle of radius? $9$ ?has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.

Problem 5

For certain real values of? $a, b, c,$ ?and? $d_{},$ ?the equation? $x^4+ax^3+bx^2+cx+d=0$ ?has four non-real roots. The product of two of these roots is? $13+i$ ?and the sum of the other two roots is? $3+4i,$ ?where? $i=sqrt{-1}.$ ?Find? $b.$

Problem 6

Let? $n=2^{31}3^{19}.$ ?How many positive integer divisors of? $n^2$ ?are less than? $n_{}$ ?but do not divide? $n_{}$ ?

Problem 7

Given that? $(1+sin t)(1+cos t)=5/4$ ?and

$(1-sin t)(1-cos t)=frac mn-sqrt{k},$ where? $k, m,$ ?and? $n_{}$ ?are positive integers with? $m_{}$ ?and? $n_{}$ ?relatively prime, find? $k+m+n.$

Problem 8

For how many ordered pairs of positive integers? $(x,y),$ ?with? $y<xle 100,$ ?are both? $frac xy$ ?and? $frac{x+1}{y+1}$ ?integers?

Problem 9

Triangle? $ABC$ ?is isosceles, with? $AB=AC$ ?and altitude? $AM=11.$ ?Suppose that there is a point? $D$ ?on? $overline{AM}$ ?with? $AD=10$ ?and? $angle BDC=3angle BAC.$ ?Then the perimeter of? $triangle ABC$ ?may be written in the form? $a+sqrt{b},$ ?where? $a$ ?and? $b$ ?are integers. Find? $a+b.$

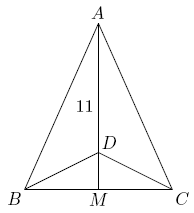
AIME 1995 Problem 9.png

Problem 10

What is the largest positive integer that is not the sum of a positive integral multiple of 42 and a positive composite integer?

Problem 11

A right rectangular prism? $P_{}$ ?(i.e., a rectangular parallelepiped) has sides of integral length? $a, b, c,$ ?with? $ale ble c.$ ?A plane parallel to one of the faces of? $P_{}$ ?cuts? $P_{}$ ?into two prisms, one of which is similar to? $P_{},$ ?and both of which have nonzero volume. Given that? $b=1995,$ ?for how many ordered triples? $(a, b, c)$ ?does such a plane exist?

Problem 12

Pyramid? $OABCD$ ?has square base? $ABCD,$ ?congruent edges? $overline{OA}, overline{OB}, overline{OC},$ ?and? $overline{OD},$ ?and? $angle AOB=45^circ.$ ?Let? $theta$ ?be the measure of the dihedral angle formed by faces? $OAB$ ?and? $OBC.$ ?Given that? $cos theta=m+sqrt{n},$ ?where? $m_{}$ ?and? $n_{}$ ?are integers, find? $m+n.$

Problem 13

Let? $f(n)$ ?be the integer closest to? $sqrt[4]{n}.$ ?Find? $sum_{k=1}^{1995}frac 1{f(k)}.$

Problem 14

In a circle of radius 42, two chords of length 78 intersect at a point whose distance from the center is 18. The two chords divide the interior of the circle into four regions. Two of these regions are bordered by segments of unequal lengths, and the area of either of them can be expressed uniquely in the form? $mpi-nsqrtcqle8lm,$ ?where? $m, n,$ ?and? $d_{}$ ?are positive integers and? $d_{}$ ?is not divisible by the square of any prime number. Find? $m+n+d.$

Problem 15

Let? $p_{}$ ?be the probability that, in the process of repeatedly flipping a fair coin, one will encounter a run of 5 heads before one encounters a run of 2 tails. Given that? $p_{}$ ?can be written in the form? $m/n$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers, find? $m+n$ .

1995AIME 詳細解析

The sum of the areas of the?squares?if they were not interconnected is a?geometric sequence:

$1^2 + left(frac{1}{2}right)^2 + left(frac{1}{4}right)^2 + left(frac{1}{8}right)^2 + left(frac{1}{16}right)^2$

Then subtract the areas of the intersections, which is? $left(frac{1}{4}right)^2 + ldots + left(frac{1}{32}right)^2$ :

$1^2 + left(frac{1}{2}right)^2 + left(frac{1}{4}right)^2 + left(frac{1}{8}right)^2 + left(frac{1}{16}right)^2 - left[left(frac{1}{4}right)^2 + left(frac{1}{8}right)^2 + left(frac{1}{16}right)^2 + left(frac{1}{32}right)^2right]$

$= 1 + frac{1}{2}^2 - frac{1}{32}^2$

The majority of the terms cancel, leaving? $1 + frac{1}{4} - frac{1}{1024}$ , which simplifies down to? $frac{1024 + left(256 - 1right)}{1024}$ . Thus,? $m-n = boxed{255}$ .

Alternatively, take the area of the first square and add? $,frac{3}{4}$ ?of the areas of the remaining squares. This results in? $1+ frac{3}{4}left[left(frac{1}{2}right)^2 + ldots + left(frac{1}{16}^2right)right]$ , which when simplified will produce the same answer.
Taking the? $log_{1995}$ ?(logarithm) of both sides and then moving to one side yields the?quadratic equation? $2(log_{1995}x)^2 - 4(log_{1995}x) + 1 = 0$ . Applying the?quadratic formula?yields that? $log_{1995}x = 1 pm frac{sqrt{2}}{2}$ . Thus, the product of the two roots (both of which are positive) is? $1995^{1+sqrt{2}/2} cdot 1995^{1 - sqrt{2}/2} = 1995^2$ , making the solution? $(2000-5)^2 equiv boxed{025} pmod{1000}$ .
It takes an even number of steps for the object to reach? $(2,2)$ , so the number of steps the object may have taken is either? $4$ ?or? $6$ .If the object took? $4$ ?steps, then it must have gone two steps?N?and two steps?E, in some permutation. There are? $frac{4!}{2!2!} = 6$ ?ways for these four steps of occuring, and the probability is? $frac{6}{4^{4}}$ .If the object took? $6$ ?steps, then it must have gone two steps?N?and two steps?E, and an additional pair of moves that would cancel out, either?N/S?or?W/E. The sequences?N,N,N,E,E,S?can be permuted in? $frac{6!}{3!2!1!} = 60$ ?ways. However, if the first four steps of the sequence are?N,N,E,E?in some permutation, it would have already reached the point? $(2,2)$ ?in four moves. There are? $frac{4!}{2!2!}$ ?ways to order those four steps and? $2!$ ?ways to determine the order of the remaining two steps, for a total of? $12$ ?sequences that we have to exclude. This gives? $60-12=48$ ?sequences of steps. There are the same number of sequences for the steps?N,N,E,E,E,W, so the probability here is? $frac{2 times 48}{4^6}$ .The total probability is? $frac{6}{4^4} + frac{96}{4^6} = frac{3}{64}$ , and? $m+n= boxed{067}$ .
We label the points as following: the centers of the circles of radii? $3,6,9$ ?are? $O_3,O_6,O_9$ ?respectively, and the endpoints of the chord are? $P,Q$ . Let? $A_3,A_6,A_9$ ?be the feet of the?perpendiculars?from? $O_3,O_6,O_9$ ?to? $overline{PQ}$ ?(so? $A_3,A_6$ ?are the points of?tangency). Then we note that? $overline{O_3A_3} parallel overline{O_6A_6} parallel overline{O_9A_9}$ , and? $O_6O_9?: O_9O_3 = 3:6 = 1:2$ . Thus,? $O_9A_9 = frac{2 cdot O_6A_6 + 1 cdot O_3A_3}{3} = 5$ ?(consider similar triangles). Applying the?Pythagorean Theorem?to? $triangle O_9A_9P$ , we find that $[PQ^2 = 4(A_9P)^2 = 4[(O_9P)^2-(O_9A_9)^2] = 4[9^2-5^2] = boxed{224}]$ $[asy] pointpen = black; pathpen = black + linewidth(0.7); size(150); pair A=(0,0), B=(6,0), C=(-3,0), D=C+6*expi(acos(1/3)), F=B+3*expi(acos(1/3)),G=5*expi(acos(1/3)), P=IP(F--F+3*(D-F),CR(A,9)), Q=IP(F--F+3*(F-D),CR(A,9)); D(CR(D(MP("O_9",A)),9)); D(CR(D(MP("O_3",B)),3)); D(CR(D(MP("O_6",C)),6)); D(MP("P",P,NW)--MP("Q",Q,NE)); D((-9,0)--(9,0)); D(A--MP("A_9",G,N)); D(B--MP("A_3",F,N)); D(C--MP("A_6",D,N)); D(A--P); D(rightanglemark(A,G,P,12)); [/asy]$
Since the?coefficients?of the?polynomial?are real, it follows that the non-real roots must come in?complex conjugate?pairs. Let the first two roots be? $m,n$ . Since? $m+n$ ?is not real,? $m,n$ ?are not conjugates, so the other pair of roots must be the conjugates of? $m,n$ . Let? $m'$ ?be the conjugate of? $m$ , and? $n'$ ?be the conjugate of? $n$ . Then, $[mcdot n = 13 + i,m' + n' = 3 + 4iLongrightarrow m'cdot n' = 13 - i,m + n = 3 - 4i.]$ By?Vieta's formulas, we have that? $b = mm' + nn' + mn' + nm' + mn + m'n' = (m + n)(m' + n') + mn + m'n' = boxed{051}$ .
We know that? $n^2 = 2^{62}3^{38}$ ?must have? $(62+1)times (38+1)$ ?factors?by its?prime factorization. If we group all of these factors (excluding? $n$ ) into pairs that multiply to? $n^2$ , then one factor per pair is less than? $n$ , and so there are? $frac{63times 39-1}{2} = 1228$ ?factors of? $n^2$ ?that are less than? $n$ . There are? $32times20-1 = 639$ ?factors of? $n$ , which clearly are less than? $n$ , but are still factors of? $n$ . Therefore, using complementary counting, there are? $1228-639=boxed{589}$ ?factors of? $n^2$ ?that do not divide? $n$ .
From the givens,? $2sin t cos t + 2 sin t + 2 cos t = frac{1}{2}$ , and adding? $sin^2 t + cos^2t = 1$ ?to both sides gives? $(sin t + cos t)^2 + 2(sin t + cos t) = frac{3}{2}$ . Completing the square on the left in the variable? $(sin t + cos t)$ ?gives? $sin t + cos t = -1 pm sqrt{frac{5}{2}}$ . Since? $|sin t + cos t| leq sqrt 2 < 1 + sqrt{frac{5}{2}}$ , we have? $sin t + cos t = sqrt{frac{5}{2}} - 1$ . Subtracting twice this from our original equation gives? $(sin t - 1)(cos t - 1) = sin t cos t - sin t - cos t + 1 = frac{13}{4} - sqrt{10}$ , so the answer is? $13 + 4 + 10 = boxed{027}$ .
Since? $y|x$ ,? $y+1|x+1$ , then? $text{gcd},(y,x)=y$ ?(the bars indicate?divisibility) and? $text{gcd},(y+1,x+1)=y+1$ . By the?Euclidean algorithm, these can be rewritten respectively as? $text{gcd},(y,x-y)=y$ ?and? $text{gcd}, (y+1,x-y)=y+1$ , which implies that both? $y,y+1 | x-y$ . Also, as? $text{gcd},(y,y+1) = 1$ , it follows that? $y(y+1)|x-y$ .?^[1]Thus, for a given value of? $y$ , we need the number of multiples of? $y(y+1)$ ?from? $0$ ?to? $100-y$ ?(as? $x le 100$ ). It follows that there are? $leftlfloorfrac{100-y}{y(y+1)} rightrfloor$ ?satisfactory positive integers for all integers? $y le 100$ . The answer is $[sum_{y=1}^{99} leftlfloorfrac{100-y}{y(y+1)} rightrfloor = 49 + 16 + 8 + 4 + 3 + 2 + 1 + 1 + 1 = boxed{085}.]$ ^?Another way of stating this is to note that if? $frac{x}{y}$ ?and? $frac{x+1}{y+1}$ ?are integers, then? $frac{x}{y} - 1 = frac{x-y}{y}$ ?and? $frac{x+1}{y+1} - 1 = frac{x-y}{y+1}$ ?must be integers. Since? $y$ ?and? $y+1$ ?cannot share common prime factors, it follows that? $frac{x-y}{y(y+1)}$ ?must also be an integer.
Let? $x=angle CAM$ , so? $3x=angle CDM$ . Then,? $frac{tan 3x}{tan x}=frac{CM/1}{CM/11}=11$ . Expanding? $tan 3x$ ?using the angle sum identity gives $[tan 3x=tan(2x+x)=frac{3tan x-tan^3x}{1-3tan^2x}.]$ Thus,? $frac{3-tan^2x}{1-3tan^2x}=11$ . Solving, we get? $tan x= frac 12$ . Hence,? $CM=frac{11}2$ ?and? $AC= frac{11sqrt{5}}2$ ?by the?Pythagorean Theorem. The total perimeter is? $2(AC + CM) = sqrt{605}+11$ . The answer is thus? $a+b=boxed{616}$ .
The requested number? $mod {42}$ ?must be a?prime?number. Also, every number that is a multiple of? $42$ ?greater than that prime number must also be prime, except for the requested number itself. So we make a table, listing all the primes up to? $42$ ?and the numbers that are multiples of? $42$ ?greater than them, until they reach a composite number. $[begin{tabular}{|r||r|r|r|r|r|} hline 2&44&&&& \ 3&45&&&& \ 5&47&89&131&173&215 \ 7&49&&&& \ 11&53&95&&& \ 13&55&&&& \ 17&59&101&143&& \ 19&61&103&145&& \ 23&65&&&& \ 29&71&113&155&& \ 31&73&115&&& \ 37&79&121&&& \ 41&83&125&&& \ hline end{tabular}]$ $boxed{215}$ ?is the greatest number in the list, so it is the answer. Note that considering? $mod {5}$ ?would have shortened the search, since? $text{gcd}(5,42)=1$ , and so within? $5$ ?numbers at least one must be divisible by? $5$ .
Let? $P'$ ?be the prism similar to? $P$ , and let the sides of? $P'$ ?be of length? $x,y,z$ , such that? $x le y le z$ . Then $[frac{x}{a} = frac{y}{b} = frac zc < 1.]$ Note that if the ratio of similarity was equal to? $1$ , we would have a prism with zero volume. As one face of? $P'$ ?is a face of? $P$ , it follows that? $P$ ?and? $P'$ ?share at least two side lengths in common. Since? $x < a, y < b, z < c$ , it follows that the only possibility is? $y=a,z=b=1995$ . Then, $[frac{x}{a} = frac{a}{1995} = frac{1995}{c} Longrightarrow ac = 1995^2 = 3^25^27^219^2.]$ The number of factors of? $3^25^27^219^2$ ?is? $(2+1)(2+1)(2+1)(2+1) = 81$ . Only in? $leftlfloor frac {81}2 rightrfloor = 40$ ?of these cases is? $a < c$ ?(for? $a=c$ , we end with a prism of zero volume). We can easily verify that these will yield nondegenerate prisms, so the answer is? $boxed{040}$ .
$[asy] import three; // calculate intersection of line and plane // p = point on line // d = direction of line // q = point in plane // n = normal to plane triple lineintersectplan(triple p, triple d, triple q, triple n) { return (p + dot(n,q - p)/dot(n,d)*d); } // projection of point A onto line BC triple projectionofpointontoline(triple A, triple B, triple C) { return lineintersectplan(B, B - C, A, B - C); } currentprojection=perspective(2,1,1); triple A, B, C, D, O, P; A = (sqrt(2 - sqrt(2)), sqrt(2 - sqrt(2)), 0); B = (-sqrt(2 - sqrt(2)), sqrt(2 - sqrt(2)), 0); C = (-sqrt(2 - sqrt(2)), -sqrt(2 - sqrt(2)), 0); D = (sqrt(2 - sqrt(2)), -sqrt(2 - sqrt(2)), 0); O = (0,0,sqrt(2*sqrt(2))); P = projectionofpointontoline(A,O,B); draw(D--A--B); draw(B--C--D,dashed); draw(A--O); draw(B--O); draw(C--O,dashed); draw(D--O); draw(A--P); draw(P--C,dashed); label("$A$", A, S); label("$B$", B, E); label("$C$", C, NW); label("$D$", D, W); label("$O$", O, N); dot("$P$", P, NE); [/asy]$ The angle? $theta$ ?is the angle formed by two?perpendiculars?drawn to? $BO$ , one on the plane determined by? $OAB$ ?and the other by? $OBC$ . Let the perpendiculars from? $A$ ?and? $C$ ?to? $overline{OB}$ ?meet? $overline{OB}$ ?at? $P.$ ?Without loss of generality, let? $AP = 1.$ ?It follows that? $triangle OPA$ ?is a? $45-45-90$ ?right triangle, so? $OP = AP = 1,$ ? $OB = OA = sqrt {2},$ ?and? $AB = sqrt {4 - 2sqrt {2}}.$ ?Therefore,? $AC = sqrt {8 - 4sqrt {2}}.$ From the?Law of Cosines,? $AC^{2} = AP^{2} + PC^{2} - 2(AP)(PC)cos theta,$ ?so $[8 - 4sqrt {2} = 1 + 1 - 2cos theta Longrightarrow cos theta = - 3 + 2sqrt {2} = - 3 + sqrt{8}.]$ Thus? $m + n = boxed{005}$ .
When? $left(k - frac {1}{2}right)^4 leq n < left(k + frac {1}{2}right)^4$ ,? $f(n) = k$ . Thus there are? $left lfloor left(k + frac {1}{2}right)^4 - left(k - frac {1}{2}right)^4 rightrfloor$ ?values of? $n$ ?for which? $f(n) = k$ . Expanding using the?binomial theorem, $begin{align*} left(k + frac {1}{2}right)^4 - left(k - frac {1}{2}right)^4 &= left(k^4 + 2k^3 + frac 32k^2 + frac 12k + frac 1{16}right) - left(k^4 - 2k^3 + frac 32k^2 - frac 12k + frac 1{16}right)\ &= 4k^3 + k. end{align*}$ Thus,? $frac{1}{k}$ ?appears in the summation? $4k^3 + k$ ?times, and the sum for each? $k$ ?is then? $(4k^3 + k) cdot frac{1}{k} = 4k^2 + 1$ . From? $k = 1$ ?to? $k = 6$ , we get? $sum_{k=1}^{6} 4k^2 + 1 = 364 + 6 = 370$ ?(either adding or using the?sum of consecutive squares formula).But this only accounts for? $sum_{k = 1}^{6} (4k^3 + k) = 4left(frac{6(6+1)}{2}right)^2 + frac{6(6+1)}{2} = 1764 + 21 = 1785$ ?terms, so we still have? $1995 - 1785 = 210$ ?terms with? $f(n) = 7$ . This adds? $210 cdot frac {1}{7} = 30$ ?to our summation, giving? ${400}$ .
Let the center of the circle be? $O$ , and the two chords be? $overline{AB}, overline{CD}$ ?and intersecting at? $E$ , such that? $AE = CE < BE = DE$ . Let? $F$ ?be the midpoint of? $overline{AB}$ . Then? $overline{OF} perp overline{AB}$ . $[asy] size(200); pathpen = black + linewidth(0.7); pen d = dashed+linewidth(0.7); pair O = (0,0), E=(0,18), B=E+48*expi(11*pi/6), D=E+48*expi(7*pi/6), A=E+30*expi(5*pi/6), C=E+30*expi(pi/6), F=foot(O,B,A); D(CR(D(MP("O",O)),42)); D(MP("A",A,NW)--MP("B",B,SE)); D(MP("C",C,NE)--MP("D",D,SW)); D(MP("E",E,N)); D(C--B--O--E,d);D(O--D(MP("F",F,NE)),d); MP("39",(B+F)/2,NE);MP("30",(C+E)/2,NW);MP("42",(B+O)/2); [/asy]$ By the?Pythagorean Theorem,? $OF = sqrt{OB^2 - BF^2} = sqrt{42^2 - 39^2} = 9sqrt{3}$ , and? $EF = sqrt{OE^2 - OF^2} = 9$ . Then? $OEF$ ?is a? $30-60-90$ ?right triangle, so? $angle OEB = angle OED = 60^{circ}$ . Thus? $angle BEC = 60^{circ}$ , and by the?Law of Cosines, $BC^2 = BE^2 + CE^2 - 2 cdot BE cdot CE cos 60^{circ} = 42^2.$ It follows that? $triangle BCO$ ?is an?equilateral triangle, so? $angle BOC = 60^{circ}$ . The desired area can be broken up into two regions,? $triangle BCE$ ?and the region bounded by? $overline{BC}$ ?and minor arc? $stackrel{frown}{BC}$ . The former can be found by?Heron's formula?to be? $[BCE] = sqrt{60(60-48)(60-42)(60-30)} = 360sqrt{3}$ . The latter is the difference between the area of?sector? $BOC$ ?and the equilateral? $triangle BOC$ , or? $frac{1}{6}pi (42)^2 - frac{42^2 sqrt{3}}{4} = 294pi - 441sqrt{3}$ .Thus, the desired area is? $360sqrt{3} + 294pi - 441sqrt{3} = 294pi - 81sqrt{3}$ , and? $m+n+d = boxed{378}$ .
Think of the problem as a sequence of?H's and?T's. No two?T's can occur in a row, so the sequence is blocks of? $1$ ?to? $4$ ?H's separated by?T's and ending in? $5$ ?H's. Since the first letter could be?T?or the sequence could start with a block of?H's, the total probability is that? $3/2$ ?of it has to start with an?H.The answer to the problem is then the sum of all numbers of the form? $frac 32 left( frac 1{2^a} cdot frac 12 cdot frac 1{2^b} cdot frac 12 cdot frac 1{2^c} cdots right) cdot left(frac 12right)^5$ , where? $a,b,c ldots$ ?are all numbers? $1-4$ , since the blocks of?H's can range from? $1-4$ ?in length. The sum of all numbers of the form? $(1/2)^a$ ?is? $1/2+1/4+1/8+1/16=15/16$ , so if there are n blocks of?H's before the final five?H's, the answer can be rewritten as the sum of all numbers of the form? $frac 32left( left(frac {15}{16}right)^n cdot left(frac 12right)^n right) cdot left(frac 1{32}right)=frac 3{64}left(frac{15}{32}right)^n$ , where? $n$ ?ranges from? $0$ ?to? $infty$ , since that's how many blocks of?H's there can be before the final five. This is an infinite geometric series whose sum is? $frac{3/64}{1-(15/32)}=frac{3}{34}$ , so the answer is? $boxed{037}$ .