Home » 國際競賽 » 數(shù)學(xué)國際競賽 » AMC美國數(shù)學(xué)競賽 » Details

1999AIME 真題及答案解析

Category: AMC美國數(shù)學(xué)競賽, 國際競賽 Date: 2019年12月11日下午6:48

1999AIME 真題及答案解析

答案解析請參考文末

Problem 1

Find the smallest prime that is the fifth term of an increasing arithmetic sequence, all four preceding terms also being prime.

Problem 2

Consider the parallelogram with vertices? $(10,45),$ ? $(10,114),$ ? $(28,153),$ ?and? $(28,84).$ ?A line through the origin cuts this figure into two congruent polygons. The slope of the line is? $m/n,$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers. Find? $m+n.$

Problem 3

Find the sum of all positive integers? $n$ ?for which? $n^2-19n+99$ ?is a perfect square.

Problem 4

The two squares shown share the same center? $O_{}$ ?and have sides of length 1. The length of? $overline{AB}$ ?is? $43/99$ ?and the area of octagon? $ABCDEFGH$ ?is? $m/n,$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers. Find? $m+n.$

AIME 1999 Problem 4.png

Problem 5

For any positive integer? $x_{}$ , let? $S(x)$ ?be the sum of the digits of? $x_{}$ , and let? $T(x)$ ?be? $|S(x+2)-S(x)|.$ ?For example,? $T(199)=|S(201)-S(199)|=|3-19|=16.$ ?How many values of? $T(x)$ ?do not exceed 1999?

Problem 6

A transformation of the first quadrant of the coordinate plane maps each point? $(x,y)$ ?to the point? $(sqrt{x},sqrt{y}).$ ?The vertices of quadrilateral? $ABCD$ ?are? $A=(900,300), B=(1800,600), C=(600,1800),$ ?and? $D=(300,900).$ ?Let? $k_{}$ ?be the area of the region enclosed by the image of quadrilateral? $ABCD.$ ?Find the greatest integer that does not exceed? $k_{}.$

Problem 7

There is a set of 1000 switches, each of which has four positions, called? $A, B, C$ , and? $D$ . When the position of any switch changes, it is only from? $A$ ?to? $B$ , from? $B$ ?to? $C$ , from? $C$ ?to? $D$ , or from? $D$ ?to? $A$ . Initially each switch is in position? $A$ . The switches are labeled with the 1000 different integers? $(2^{x})(3^{y})(5^{z})$ , where? $x, y$ , and? $z$ ?take on the values? $0, 1, ldots, 9$ . At step? $i$ ?of a 1000-step process, the? $i$ -th switch is advanced one step, and so are all the other switches whose labels divide the label on the? $i$ -th switch. After step 1000 has been completed, how many switches will be in position? $A$ ?

Problem 8

Let? $mathcal{T}$ ?be the set of ordered triples? $(x,y,z)$ ?of nonnegative real numbers that lie in the plane? $x+y+z=1.$ ?Let us say that? $(x,y,z)$ ?supports? $(a,b,c)$ ?when exactly two of the following are true:? $xge a, yge b, zge c.$ ?Let? $mathcal{S}$ ?consist of those triples in? $mathcal{T}$ ?that support? $left(frac 12,frac 13,frac 16right).$ ?The area of? $mathcal{S}$ ?divided by the area of? $mathcal{T}$ ?is? $m/n,$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers, find? $m+n.$

Problem 9

A function? $f$ ?is defined on the complex numbers by? $f(z)=(a+bi)z,$ ?where? $a_{}$ ?and? $b_{}$ ?are positive numbers. This function has the property that the image of each point in the complex plane is equidistant from that point and the origin. Given that? $|a+bi|=8$ ?and that? $b^2=m/n,$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers. Find? $m+n.$

Problem 10

Ten points in the plane are given, with no three collinear. Four distinct segments joining pairs of these points are chosen at random, all such segments being equally likely. The probability that some three of the segments form a triangle whose vertices are among the ten given points is? $m/n,$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers. Find? $m+n.$

Problem 11

Given that? $sum_{k=1}^{35}sin 5k=tan frac mn,$ ?where angles are measured in degrees, and? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers that satisfy? $frac mn<90,$ ?find? $m+n.$

Problem 12

The inscribed circle of triangle? $ABC$ ?is tangent to? $overline{AB}$ ?at? $P_{},$ ?and its radius is 21. Given that? $AP=23$ ?and? $PB=27,$ ?find the perimeter of the triangle.

Problem 13

Forty teams play a tournament in which every team plays every other( $39$ ?different opponents) team exactly once. No ties occur, and each team has a? $50 %$ ?chance of winning any game it plays. The probability that no two teams win the same number of games is? $m/n,$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers. Find? $log_2 n.$

Problem 14

Point? $P_{}$ ?is located inside triangle? $ABC$ ?so that angles? $PAB, PBC,$ ?and? $PCA$ ?are all congruent. The sides of the triangle have lengths? $AB=13, BC=14,$ ?and? $CA=15,$ ?and the tangent of angle? $PAB$ ?is? $m/n,$ ?where? $m_{}$ ?and? $n_{}$ ?are relatively prime positive integers. Find? $m+n.$

Problem 15

Consider the paper triangle whose vertices are? $(0,0), (34,0),$ ?and? $(16,24).$ ?The vertices of its midpoint triangle are the midpoints of its sides. A triangular pyramid is formed by folding the triangle along the sides of its midpoint triangle. What is the volume of this pyramid?

1999AIME 詳細(xì)解析

Obviously, all of the terms must be?odd. The common difference between the terms cannot be? $2$ ?or? $4$ , since otherwise there would be a number in the sequence that is divisible by? $3$ . However, if the common difference is? $6$ , we find that? $5,11,17,23$ , and? $29$ ?form an?arithmetic sequence. Thus, the answer is? $029$ .
Let the first point on the line? $x=10$ ?be? $(10,45+a)$ ?where a is the height above? $(10,45)$ . Let the second point on the line? $x=28$ ?be? $(28, 153-a)$ . For two given points, the line will pass the origin if the coordinates are?proportional?(such that? $frac{y_1}{x_1} = frac{y_2}{x_2}$ ). Then, we can write that? $frac{45 + a}{10} = frac{153 - a}{28}$ . Solving for? $a$ ?yields that? $1530 - 10a = 1260 + 28a$ , so? $a=frac{270}{38}=frac{135}{19}$ . The slope of the line (since it passes through the origin) is? $frac{45 + frac{135}{19}}{10} = frac{99}{19}$ , and the solution is? $m + n = boxed{118}$ .
If? $n^2-19n+99=x^2$ ?for some positive integer? $x$ , then rearranging we get? $n^2-19n+99-x^2=0$ . Now from the quadratic formula,

$n=frac{19pm sqrt{4x^2-35}}{2}$

Because? $n$ ?is an integer, this means? $4x^2-35=q^2$ ?for some nonnegative integer? $q$ . Rearranging gives? $(2x+q)(2x-q)=35$ . Thus? $(2x+q, 2x-q)=(35, 1)$ ?or? $(7,5)$ , giving? $x=3$ ?or? $9$ . This gives? $n=1, 9, 10,$ ?or? $18$ , and the sum is? $1+9+10+18=boxed{38}$ .

Suppose there is some? $k$ ?such that? $x^2 - 19x + 99 = k^2$ . Completing the square, we have that? $(x - 19/2)^2 + 99 - (19/2)^2 = k^2$ , that is,? $(x - 19/2)^2 + 35/4 = k^2$ . Multiplying both sides by 4 and rearranging, we see that? $(2k)^2 - (2x - 19)^2 = 35$ . Thus,? $(2k - 2x + 19)(2k + 2x - 19) = 35$ . We then proceed as we did in the previous solution.
Triangles? $AOB$ ,? $BOC$ ,? $COD$ , etc. are congruent by symmetry (you can prove it rigorously with congruent triangles), and each area is? $frac{frac{43}{99}cdotfrac{1}{2}}{2}$ . Since the area of a triangle is? $bh/2$ , the area of all? $8$ ?of them is? $frac{86}{99}$ ?and the answer is? $boxed{185}$ .Define the two possible?distances?from one of the labeled points and the?corners?of the square upon which the point lies as? $x$ ?and? $y$ . The area of the?octagon?(by?subtraction?of areas) is? $1 - 4left(frac{1}{2}xyright) = 1 - 2xy$ .By the?Pythagorean theorem, $[x^2 + y^2 = left(frac{43}{99}right)^2]$ Also, $begin{align*}x + y + frac{43}{99} &= 1\ x^2 + 2xy + y^2 &= left(frac{56}{99}right)^2end{align*}$ Substituting, $begin{align*}left(frac{43}{99}right)^2 + 2xy &= left(frac{56}{99}right)^2 \ 2xy = frac{(56 + 43)(56 - 43)}{99^2} &= frac{13}{99} end{align*}$
Thus, the area of the octagon is? $1 - frac{13}{99} = frac{86}{99}$ , so? $m + n = boxed{185}$ .]
For most values of? $x$ ,? $T(x)$ ?will equal? $2$ . For those that don't, the difference must be bumping the number up a ten, a hundred, etc. If we take? $T(a999)$ ?as an example, $[|(a + 1) + 0 + 0 + 1 - (a + 9 + 9 + 9)| = |2 - 9(3)|]$ And in general, the values of? $T(x)$ ?will then be in the form of? $|2 - 9n| = 9n - 2$ . From? $7$ ?to? $1999$ , there are? $leftlceil frac{1999 - 7}{9}rightrceil = 222$ ?solutions; including? $2$ ?and there are a total of? $boxed{223}$ ?solutions.
$begin{eqnarray*}A' = & (sqrt {900}, sqrt {300})\ B' = & (sqrt {1800}, sqrt {600})\ C' = & (sqrt {600}, sqrt {1800})\ D' = & (sqrt {300}, sqrt {900}) end{eqnarray*}$ First we see that lines passing through? $AB$ ?and? $CD$ ?have?equations? $y = frac {1}{3}x$ ?and? $y = 3x$ , respectively. Looking at the points above, we see the equations for? $A'B'$ ?and? $C'D'$ ?are? $y^2 = frac {1}{3}x^2$ ?and? $y^2 = 3x^2$ , or, after manipulation? $y = frac {x}{sqrt {3}}$ ?and? $y = sqrt {3}x$ , respectively, which are still linear functions. Basically the square of the image points gives back the original points and we could plug them back into the original equation to get the equation of the image lines.Now take a look at? $BC$ ?and? $AD$ , which have the equations? $y = - x + 2400$ ?and? $y = - x + 1200$ . The image equations hence are? $x^2 + y^2 = 2400$ ?and? $x^2 + y^2 = 1200$ , respectively, which are the equations for?circles.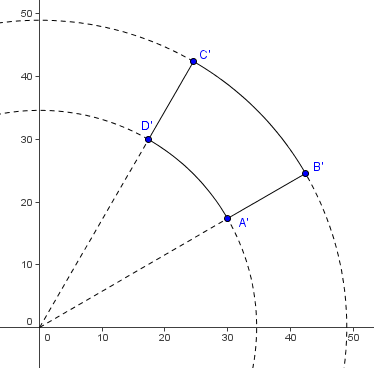To find the area between the circles (actually, parts of the circles), we need to figure out the?angle?of the?arc. This could be done by? $arctan sqrt {3} - arctan frac {1}{sqrt {3}} = 60^circ - 30^circ = 30^circ$ . So the requested areas are the area of the enclosed part of the smaller circle subtracted from the area enclosed by the part of the larger circle =? $frac {30^circ}{360^circ}(R^2pi - r^2pi) = frac {1}{12}(2400pi - 1200pi) = 100pi$ . Hence the answer is? $boxed{314}$ .
For each?th switch (designated by?), it advances?itself?only one time at the?th step; thereafter, only a switch with larger??values will advance the?th switch by one step provided??divides?. Let??be the max switch label. To find the divisor multiples in the range of??to?, we consider the exponents of the number?. In general, the divisor-count of??must be a multiple of 4 to ensure that a switch is in position A: $4n = [(9-x)+1] [(9-y)+1] [(9-z)+1] = (10-x)(10-y)(10-z)$ , where? $0 le x,y,z le 9.$ We consider the cases where the 3 factors above do not contribute multiples of 4.
- Case of no 2's:
The switches must be? $(mathrm{odd})(mathrm{odd})(mathrm{odd})$ . There are? $5$ ?odd integers?in? $0$ ?to? $9$ , so we have? $5 times 5 times 5 = 125$ ?ways.
- Case of a single 2:
The switches must be one of? $(2cdot mathrm{odd})(mathrm{odd})(mathrm{odd})$ ?or? $(mathrm{odd})(2 cdot mathrm{odd})(mathrm{odd})$ ?or? $(mathrm{odd})(mathrm{odd})(2 cdot mathrm{odd})$ .

Since? $0 le x,y,z le 9,$ ?the terms? $2cdot 1, 2 cdot 3,$ ?and? $2 cdot 5$ ?are three valid choices for the? $(2 cdot odd)$ ?factor above.

We have? ${3choose{1}} cdot 3 cdot 5^{2}= 225$ ?ways.

The number of switches in position A is? $1000-125-225 = boxed{650}$ .
This problem just requires a good diagram and strong 3D visualization.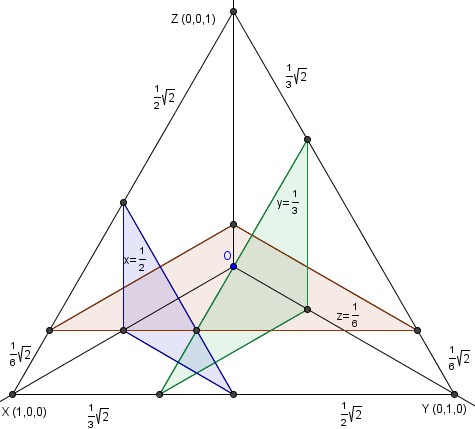The region in? $(x,y,z)$ ?where? $x ge frac{1}{2}, y ge frac{1}{3}$ ?is that of a little triangle on the bottom of the above diagram, of? $y ge frac{1}{3}, z ge frac{1}{6}$ ?is the triangle at the right, and? $x ge frac 12, z ge frac 16$ ?the triangle on the left, where the triangles are coplanar with the large equilateral triangle formed by? $x+y+z=1, x,y,z ge 0$ . We can check that each of the three regions mentioned fall under exactly two of the inequalities and not the third.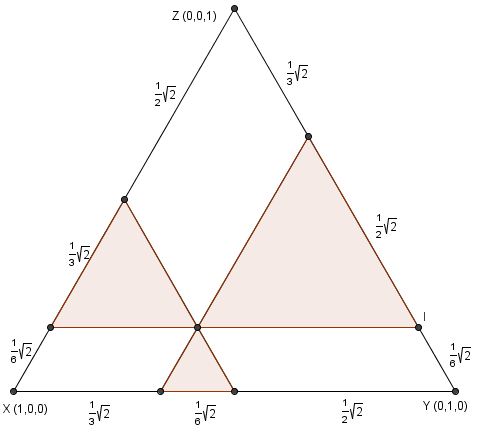The side length of the large equilateral triangle is? $sqrt{2}$ , which we can find using 45-45-90? $triangle$ ?with the axes. Using the formula? $A = frac{s^2sqrt{3}}{4}$ ?for?equilateral triangles, the area of the large triangle is? $frac{(sqrt{2})^2sqrt{3}}{4} = frac{sqrt{3}}{2}$ . Since the lines of the smaller triangles are?parallel?to those of the large triangle, by corresponding angles we see that all of the triangles are?similar, so they are all equilateral triangles. We can solve for their side lengths easily by subtraction, and we get? $frac{sqrt{2}}{6}, frac{sqrt{2}}{3}, frac{sqrt{2}}{2}$ . Calculating their areas, we get? $frac{sqrt{3}}{8}, frac{sqrt{3}}{18}, frac{sqrt{3}}{72}$ . The?ratio? $frac{mathcal{S}}{mathcal{T}} = frac{frac{9sqrt{3} + 4sqrt{3} + sqrt{3}}{72}}{frac{sqrt{3}}{2}} = frac{14}{36} = frac{7}{18}$ , and the answer is? $m + n = boxed{025}$ .
To simplify the problem, we could used the fact that the area ratios are equal to the side ratios squared, and we get? $left(frac{1}{2}right)^2 + left(frac{1}{3}right)^2 + left(frac{1}{6}right)^2 = frac{14}{36} = frac{7}{18}$ .
Suppose we pick an arbitrary point on the?complex plane, say? $(1,1)$ . According to the definition of? $f(z)$ , $[f(1+i) = (a+bi)(1+i) = (a-b) + (a+b)i,]$ this image must be equidistant to? $(1,1)$ ?and? $(0,0)$ . Thus the image must lie on the line with slope? $-1$ ?and which passes through? $left(frac 12, frac12right)$ , so its graph is? $x + y = 1$ . Substituting? $x = (a-b)$ ?and? $y = (a+b)$ , we get? $2a = 1 Rightarrow a = frac 12$ .By the?Pythagorean Theorem, we have? $left(frac{1}{2}right)^2 + b^2 = 8^2 Longrightarrow b^2 = frac{255}{4}$ , and the answer is? $boxed{259}$ .Plugging in? $z=1$ ?yields? $f(1) = a+bi$ . This implies that? $a+bi$ ?must fall on the line? $Re(z)=a=frac{1}{2}$ , given the equidistant rule. By? $|a+bi|=8$ , we get? $a^2 + b^2 = 64$ , and plugging in? $a=frac{1}{2}$ ?yields? $b^2=frac{255}{4}$ . The answer is thus? $boxed{259}$ .We are given that? $(a + bi)z$ ?is equidistant from the origin and? $z.$ ?This translates to $begin{eqnarray*} |(a + bi)z - z| & = & |(a + bi)z| \ |z(a - 1) + bzi| & = & |az + bzi| \ |z||(a - 1) + bi| & = & |z||a + bi| \ (a - 1)^2 + b^2 & = & a^2 + b^2 \ & Rightarrow & a = frac 12 end{eqnarray*}$ Since? $|a + bi| = 8,$ ? $a^2 + b^2 = 64.$ ?But? $a = frac 12,$ ?thus? $b^2 = frac {255}4.$ ?So the answer is? $259$ .
First, let us find the number of triangles that can be formed from the 10 points. Since none of the points are collinear, it is possible to pick? ${10choose3}$ ?sets of 3 points which form triangles. However, a fourth distinct segment must also be picked. Since the triangle accounts for 3 segments, there are? $45 - 3 = 42$ ?segments remaining.The total number of ways of picking four distinct segments is? ${45choose4}$ . Thus, the requested probability is? $frac{{10choose3} cdot 42}{{45choose4}} = frac{10 cdot 9 cdot 8 cdot 42 cdot 4!}{45 cdot 44 cdot 43 cdot 42 cdot 3!} = frac{16}{473}$ . The solution is? $m + n = 489$ .Note that 4 points can NEVER form 2 triangles. Therefore, we just need to multiply the probability that the first three segments picked form a triangle by 4. We can pick any segment for the first choice, then only segments that share an endpoint with the first one, then the one segment that completes the triangle. Note that the fourth segment doesn't matter in this case. Note that there are? $(9 - 1) times 2 = 16$ ?segments that share an endpoint with the first segment. The answer is then? $4 times frac{16}{44} times frac{1}{43} = frac{16}{11} times frac{1}{43} = frac{16}{473} implies m + n = boxed{489}$ -
Let? $s = sum_{k=1}^{35}sin 5k = sin 5 + sin 10 + ldots + sin 175$ . We could try to manipulate this sum by wrapping the terms around (since the first half is equal to the second half), but it quickly becomes apparent that this way is difficult to pull off. Instead, we look to?telescope?the sum. Using the?identity? $sin a sin b = frac 12(cos (a-b) - cos (a+b))$ , we can rewrite? $s$ ?as $[s cdot sin 5 = sum_{k=1}^{35} sin 5k sin 5 = sum_{k=1}^{35} frac{1}{2}(cos (5k - 5)- cos (5k + 5))]$ $[s = frac{0.5(cos 0 - cos 10 + cos 5 - cos 15 + cos 10 - cos 20 + ldots - cos 170 + cos 165 - cos 175+ cos 170 - cos 180)}{sin 5}]$ This telescopes to? $s = frac{cos 0 + cos 5 - cos 175 - cos 180}{2 sin 5} = frac{1 + cos 5}{sin 5}$ . Manipulating this to use the identity? $tan x = frac{1 - cos 2x}{sin 2x}$ , we get? $s = frac{1 - cos 175}{sin 175} Longrightarrow s = tan frac{175}{2}$ , and our answer is? $boxed{177}$ .
$[asy] pathpen = black + linewidth(0.65); pointpen = black; pair A=(0,0),B=(50,0),C=IP(circle(A,23+245/2),circle(B,27+245/2)), I=incenter(A,B,C); path P = incircle(A,B,C); D(MP("A",A)--MP("B",B)--MP("C",C,N)--cycle);D(P); D(MP("P",IP(A--B,P))); pair Q=IP(C--A,P),R=IP(B--C,P); D(MP("R",R,NE));D(MP("Q",Q,NW)); MP("23",(A+Q)/2,W);MP("27",(B+R)/2,E); [/asy]$ Let? $Q$ ?be the tangency point on? $overline{AC}$ , and? $R$ ?on? $overline{BC}$ . By the?Two Tangent Theorem,? $AP = AQ = 23$ ,? $BP = BR = 27$ , and? $CQ = CR = x$ . Using? $rs = A$ , where? $s = frac{27 cdot 2 + 23 cdot 2 + x cdot 2}{2} = 50 + x$ , we get? $(21)(50 + x) = A$ . By?Heron's formula,? $A = sqrt{s(s-a)(s-b)(s-c)} = sqrt{(50+x)(x)(23)(27)}$ . Equating and squaring both sides, $begin{eqnarray*} [21(50+x)]^2 &=& (50+x)(x)(621)\ 441(50+x) &=& 621x\ 180x = 441 cdot 50 &Longrightarrow & x = frac{245}{2} end{eqnarray*}$ We want the perimeter, which is? $2s = 2left(50 + frac{245}{2}right) = boxed{345}$ .Let the incenter be denoted? $I$ . It is commonly known that the incenter is the intersection of the angle bisectors of a triangle. So let? $angle ABI = angle CBI = alpha, angle BAI = angle CAI = beta,$ ?and? $angle BCI = angle ACI = gamma.$ We have that $begin{eqnarray*} tan alpha & = & frac {21}{27} \ tan beta & = & frac {21}{23} \ tan gamma & = & frac {21}x. end{eqnarray*}$ So naturally we look at? $tan gamma.$ ?But since? $gamma = frac pi2 - (beta + alpha)$ ?we have $begin{eqnarray*} tan gamma & = & tanleft(frac pi2 - (beta + alpha)right) \ & = & frac 1{tan(alpha + beta)} \ Rightarrow frac {21}x & = & frac {1 - frac {21cdot 21}{23cdot 27}}{frac {21}{27} + frac {21}{23}} end{eqnarray*}$ Doing the algebra, we get? $x = frac {245}2.$
The perimeter is therefore? $2cdotfrac {245}2 + 2cdot 23 + 2cdot 27 = boxed{345}.$
There are? ${40 choose 2} = 780$ ?total pairings of teams, and thus? $2^{780}$ ?possible outcomes. In order for no two teams to win the same number of games, they must each win a different number of games. Since the minimum and maximum possible number of games won are 0 and 39 respectively, and there are 40 teams in total, each team corresponds uniquely with some? $k$ , with? $0 leq k leq 39$ , where? $k$ ?represents the number of games the team won. With this in mind, we see that there are a total of? $40!$ ?outcomes in which no two teams win the same number of games. Further, note that these are all the valid combinations, as the team with 1 win must beat the team with 0 wins, the team with 2 wins must beat the teams with 1 and 0 wins, and so on; thus, this uniquely defines a combination.The desired probability is thus? $frac{40!}{2^{780}}$ . We wish to simplify this into the form? $frac{m}{n}$ , where? $m$ ?and? $n$ ?are relatively prime. The only necessary step is to factor out all the powers of 2 from? $40!$ ; the remaining number is clearly relatively prime to all powers of 2.The number of powers of 2 in? $40!$ ?is? $left lfloor frac{40}{2} right rfloor + left lfloor frac{40}{4} right rfloor + left lfloor frac{40}{8} right rfloor + left lfloor frac{40}{16} right rfloor + left lfloor frac{40}{32} right rfloor = 20 + 10 + 5 + 2 + 1 = 38.$ $780-38 = boxed{742}$ .
Drop?perpendiculars?from? $P$ ?to the three sides of? $triangle ABC$ ?and let them meet? $overline{AB}, overline{BC},$ ?and? $overline{CA}$ ?at? $D, E,$ ?and? $F$ ?respectively. $[asy] import olympiad; real theta = 29.66115; /* arctan(168/295) to five decimal places .. don't know other ways to construct Brocard */ pathpen = black +linewidth(0.65); pointpen = black; pair A=(0,0),B=(13,0),C=IP(circle(A,15),circle(B,14)); D(MP("A",A)--MP("B",B)--MP("C",C,N)--cycle); /* constructing P, C is there as check */ pair Aa=A+(B-A)*dir(theta),Ba=B+(C-B)*dir(theta),Ca=C+(A-C)*dir(theta), P=IP(A--Aa,B--Ba); D(A--MP("P",P,SSW)--B);D(P--C); D(anglemark(B,A,P,30));D(anglemark(C,B,P,30));D(anglemark(A,C,P,30)); MP("13",(A+B)/2,S);MP("15",(A+C)/2,NW);MP("14",(C+B)/2,NE); /* constructing D,E,F as foot of perps from P */ pair D=foot(P,A,B),E=foot(P,B,C),F=foot(P,C,A); D(MP("D",D,NE)--P--MP("E",E,SSW),dashed);D(P--MP("F",F),dashed); D(rightanglemark(P,E,C,15));D(rightanglemark(P,F,C,15));D(rightanglemark(P,D,A,15)); [/asy]$ Let? $BE = x, CF = y,$ ?and? $AD = z$ . We have that $begin{align*}DP&=ztantheta\ EP&=xtantheta\ FP&=ytanthetaend{align*}$ We can then use the tool of calculating area in two ways $begin{align*}[ABC]&=[PAB]+[PBC]+[PCA]\ &=frac{1}{2}(13)(ztantheta)+frac{1}{2}(14)(xtantheta)+frac{1}{2}(15)(ytantheta)\ &=frac{1}{2}tantheta(13z+14x+15y)end{align*}$ On the other hand, $begin{align*}[ABC]&=sqrt{s(s-a)(s-b)(s-c)}\ &=sqrt{21cdot6cdot7cdot8}\ &=84end{align*}$ We still need? $13z+14x+15y$ ?though. We have all these?right triangles?and we haven't even touched?Pythagoras. So we give it a shot: $begin{align}x^2+x^2tan^2theta&=z^2tan^2theta+(13-z)^2\ z^2+z^2tan^2theta&=y^2tan^2theta+(15-y)^2\ y^2+y^2tan^2theta&=x^2tan^2theta+(14-x)^2end{align}$ Adding? $(1) + (2) + (3)$ ?gives $begin{align*}x^2+y^2+z^2&=(14-x)^2+(15-y)^2+(13-z)^2\ Rightarrow13z+14x+15y&=295end{align*}$ Recall that we found that? $[ABC]=frac{1}{2}tantheta(13z+14x+15y)=84$ . Plugging in? $13z+14x+15y=295$ , we get? $tantheta=frac{168}{295}$ , giving us? $boxed{463}$ ?for an answer.
Let? $D$ ,? $E$ ,? $F$ ?be the feet of the altitudes to sides? $BC$ ,? $CA$ ,? $AB$ , respectively, of? $triangle ABC$ . The base of the?tetrahedron?is the?orthocenter? $O$ ?of the large triangle, so we just need to find that, then it's easy from there. The reason why we find the orthocenter is due to the fact that once we fold the tetrahedron, finding the height requires perpendicular segments that are parallel to the large sides of the large triangle.To find the coordinates of? $O$ , we need to find the intersection point of altitudes? $BE$ ?and? $AD$ . The equation of? $BE$ ?is simply? $x=16$ .? $AD$ ?is?perpendicular?to line? $BC$ , so the slope of? $AD$ ?is equal to the negative reciprocal of the slope of? $BC$ .? $BC$ ?has slope? $frac{24-0}{16-34}=-frac{4}{3}$ , therefore? $y=frac{3}{4} x$ . These two lines intersect at? $(16,12)$ , so that's the base of the height of the tetrahedron.Let? $S$ ?be the foot of altitude? $BS$ ?in? $triangle BPQ$ . From the?Pythagorean Theorem,? $h=sqrt{BS^2-SO^2}$ . However, since? $S$ ?and? $O$ ?are, by coincidence, the same point,? $SO=0$ ?and? $h=12$ .The area of the base is? $102$ , so the volume is? $frac{102*12}{3}=boxed{408}$ .