Home » 國際競賽 » 數(shù)學(xué)國際競賽 » AMC美國數(shù)學(xué)競賽 » Details

2007 AMC12A 真題及答案詳細(xì)解析

Category: AMC美國數(shù)學(xué)競賽, 國際競賽 Date: 2019年12月6日上午9:45

2007 AMC 12 A 真題

答案詳細(xì)解析請參考文末

Problem 1

One ticket to a show costs? $20$ ?at full price. Susan buys 4 tickets using a coupon that gives her a 25% discount. Pam buys 5 tickets using a coupon that gives her a 30% discount. How many more dollars does Pam pay than Susan?

$mathrm{(A)} 2qquad mathrm{(B)} 5qquad mathrm{(C)} 10qquad mathrm{(D)} 15qquad mathrm{(E)} 20$

Problem 2

An aquarium has a?rectangular base?that measures 100 cm by 40 cm and has a height of 50 cm. It is filled with water to a height of 40 cm. A brick with a rectangular base that measures 40 cm by 20 cm and a height of 10 cm is placed in the aquarium. By how many centimeters does the water rise?

$mathrm{(A)} 0.5qquad mathrm{(B)} 1qquad mathrm{(C)} 1.5qquad mathrm{(D)} 2qquad mathrm{(E)} 2.5$

Problem 3

The larger of two consecutive odd integers is three times the smaller. What is their sum?

$mathrm{(A)} 4qquad mathrm{(B)} 8qquad mathrm{(C)} 12qquad mathrm{(D)} 16qquad mathrm{(E)} 20$

Problem 4

Kate rode her bicycle for 30 minutes at a speed of 16 mph, then walked for 90 minutes at a speed of 4 mph. What was her overall average speed in miles per hour?

$mathrm{(A)} 7qquad mathrm{(B)} 9qquad mathrm{(C)} 10qquad mathrm{(D)} 12qquad mathrm{(E)} 14$

Problem 5

Last year Mr. Jon Q. Public received an inheritance. He paid? $20%$ ?in federal taxes on the inheritance, and paid? $10%$ ?of what he had left in state taxes. He paid a total of? $textdollar10,500$ ?for both taxes. How many dollars was his inheritance?

$(mathrm {A}) 30,000 qquad (mathrm {B}) 32,500 qquad (mathrm {C}) 35,000 qquad (mathrm {D}) 37,500 qquad (mathrm {E}) 40,000$

Problem 6

Triangles? $ABC$ ?and? $ADC$ ?are?isosceles?with? $AB=BC$ ?and? $AD=DC$ . Point? $D$ ?is inside triangle? $ABC$ , angle? $ABC$ ?measures 40 degrees, and angle? $ADC$ ?measures 140 degrees. What is the degree measure of angle? $BAD$ ?

$mathrm{(A)} 20qquad mathrm{(B)} 30qquad mathrm{(C)} 40qquad mathrm{(D)} 50qquad mathrm{(E)} 60$

Problem 7

Let? $a, b, c, d$ , and? $e$ ?be five consecutive terms in an arithmetic sequence, and suppose that? $a+b+c+d+e=30$ . Which of? $a, b, c, d,$ ?or? $e$ can be found?

$textrm{(A)} aqquad textrm{(B)} bqquad textrm{(C)} cqquad textrm{(D)} dqquad textrm{(E)} e$

Problem 8

A star-polygon?is drawn on a clock face by drawing a?chord?from each number to the fifth number counted clockwise from that number. That is, chords are drawn from 12 to 5, from 5 to 10, from 10 to 3, and so on, ending back at 12. What is the degree measure of the?angle?at each?vertexin the star polygon?

$mathrm{(A)} 20qquad mathrm{(B)} 24qquad mathrm{(C)} 30qquad mathrm{(D)} 36qquad mathrm{(E)} 60$

Problem 9

Yan is somewhere between his home and the stadium. To get to the stadium he can walk directly to the stadium, or else he can walk home and then ride his bicycle to the stadium. He rides 7 times?as?fast as he walks, and both choices require the same amount of time. What is the?ratioof Yan's distance from his home to his distance from the stadium?

$mathrm{(A)} frac 23qquad mathrm{(B)} frac 34qquad mathrm{(C)} frac 45qquad mathrm{(D)} frac 56qquad mathrm{(E)} frac 78$

Problem 10

A?triangle?with side lengths in the?ratio? $3?: 4?: 5$ ?is inscribed in a?circle?with?radius?3. What is the area of the triangle?

$mathrm{(A)} 8.64qquad mathrm{(B)} 12qquad mathrm{(C)} 5piqquad mathrm{(D)} 17.28qquad mathrm{(E)} 18$

Problem 11

A finite?sequence?of three-digit integers has the property that the tens and units digits of each term are, respectively, the hundreds and tens digits of the next term, and the tens and units digits of the last term are, respectively, the hundreds and tens digits of the first term. For example, such a sequence might begin with the terms 247, 475, and 756 and end with the term 824. Let? $S$ ?be the sum of all the terms in the sequence. What is the largest?prime?factor?that always divides? $S$ ?

$mathrm{(A)} 3qquad mathrm{(B)} 7qquad mathrm{(C)} 13qquad mathrm{(D)} 37qquad mathrm{(E)} 43$

Problem 12

Integers? $a, b, c,$ ?and? $d$ , not necessarily distinct, are chosen independently and at random from 0 to 2007, inclusive. What is the?probability?that? $ad-bc$ ?is?even?

$mathrm{(A)} frac 38qquad mathrm{(B)} frac 7{16}qquad mathrm{(C)} frac 12qquad mathrm{(D)} frac 9{16}qquad mathrm{(E)} frac 58$

Problem 13

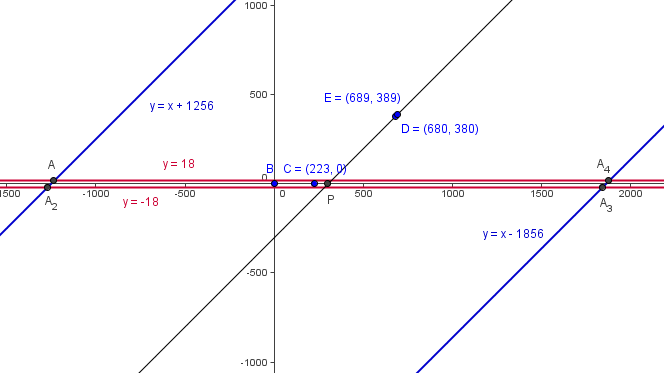
A piece of cheese is located at? $(12,10)$ ?in a?coordinate plane. A mouse is at? $(4,-2)$ ?and is running up the?line? $y=-5x+18$ . At the point? $(a,b)$ ?the mouse starts getting farther from the cheese rather than closer to it. What is? $a+b$ ?

$mathrm{(A)} 6qquad mathrm{(B)} 10qquad mathrm{(C)} 14qquad mathrm{(D)} 18qquad mathrm{(E)} 22$

Problem 14

Let a, b, c, d, and e be distinct?integers?such that

$(6-a)(6-b)(6-c)(6-d)(6-e)=45$ What is? $a+b+c+d+e$ ?

$mathrm{(A)} 5qquad mathrm{(B)} 17qquad mathrm{(C)} 25qquad mathrm{(D)} 27qquad mathrm{(E)} 30$

Problem 15

The?set? ${3,6,9,10}$ ?is augmented by a fifth element? $n$ , not equal to any of the other four. The?median?of the resulting set is equal to its?mean. What is the sum of all possible values of? $n$ ?

$mathrm{(A)} 7qquad mathrm{(B)} 9qquad mathrm{(C)} 19qquad mathrm{(D)} 24qquad mathrm{(E)} 26$

Problem 16

How many three-digit numbers are composed of three distinct digits such that one digit is the?average?of the other two?

$mathrm{(A)} 96qquad mathrm{(B)} 104qquad mathrm{(C)} 112qquad mathrm{(D)} 120qquad mathrm{(E)} 256$

Problem 17

Suppose that? $sin a + sin b = sqrt{frac{5}{3}}$ ?and? $cos a + cos b = 1$ . What is? $cos (a - b)$ ?

$mathrm{(A)} sqrt{frac{5}{3}} - 1qquad mathrm{(B)} frac 13qquad mathrm{(C)} frac 12qquad mathrm{(D)} frac 23qquad mathrm{(E)} 1$

Problem 18

The?polynomial? $f(x) = x^{4} + ax^{3} + bx^{2} + cx + d$ ?has real?coefficients, and? $f(2i) = f(2 + i) = 0.$ ?What is? $a + b + c + d?$

$mathrm{(A)} 0 qquad mathrm{(B)} 1 qquad mathrm{(C)} 4 qquad mathrm{(D)} 9 qquad mathrm{(E)} 16$

Problem 19

Triangles? $ABC$ ?and? $ADE$ ?have?areas? $2007$ ?and? $7002,$ ?respectively, with? $B = (0,0),$ ? $C = (223,0),$ ? $D = (680,380),$ ?and? $E = (689,389).$ What is the sum of all possible x-coordinates of? $A$ ?

$mathrm{(A)} 282 qquad mathrm{(B)} 300 qquad mathrm{(C)} 600 qquad mathrm{(D)} 900 qquad mathrm{(E)} 1200$

Problem 20

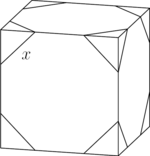
Corners are sliced off a?unit cube?so that the six?faces?each become regular?octagons. What is the total?volume?of the removed?tetrahedra?

$mathrm{(A)} frac{5sqrt{2}-7}{3}qquad mathrm{(B)} frac{10-7sqrt{2}}{3}qquad mathrm{(C)} frac{3-2sqrt{2}}{3}qquad mathrm{(D)} frac{8sqrt{2}-11}{3}qquad mathrm{(E)} frac{6-4sqrt{2}}{3}$

Problem 21

The sum of the?zeros, the product of the zeros, and the sum of the?coefficients?of the?function? $f(x)=ax^{2}+bx+c$ ?are equal. Their common value must also be which of the following?

$textrm{(A)} textrm{the coefficient of }x^{2}~~~ textrm{(B)} textrm{the coefficient of }x$ ? $textrm{(C)} textrm{the y-intercept of the graph of }y=f(x)$ ? $textrm{(D)} textrm{one of the x-intercepts of the graph of }y=f(x)$ ? $textrm{(E)} textrm{the mean of the x-intercepts of the graph of }y=f(x)$

Problem 22

For each positive integer? $n$ , let? $S(n)$ ?denote the sum of the digits of? $n.$ ?For how many values of? $n$ ?is? $n + S(n) + S(S(n)) = 2007?$

$mathrm{(A)} 1 qquad mathrm{(B)} 2 qquad mathrm{(C)} 3 qquad mathrm{(D)} 4 qquad mathrm{(E)} 5$

Problem 23

Square? $ABCD$ ?has area? $36,$ ?and? $overline{AB}$ ?is?parallel?to the?x-axis. Vertices? $A,$ ? $B$ , and? $C$ ?are on the graphs of? $y = log_{a}x,$ ? $y = 2log_{a}x,$ ?and? $y = 3log_{a}x,$ ?respectively. What is? $a?$

$mathrm{(A)} sqrt [6]{3}qquad mathrm{(B)} sqrt {3}qquad mathrm{(C)} sqrt [3]{6}qquad mathrm{(D)} sqrt {6}qquad mathrm{(E)} 6$

Problem 24

For each integer? $n>1$ , let? $F(n)$ ?be the number of solutions to the equation? $sin{x}=sin{(nx)}$ ?on the interval? $[0,pi]$ . What is? $sum_{n=2}^{2007} F(n)$ ?

$mathrm{(A)} 2014524$ ? $mathrm{(B)} 2015028$ ? $mathrm{(C)} 2015033$ ? $mathrm{(D)} 2016532$ ? $mathrm{(E)} 2017033$

Problem 25

Call a set of integers?spacy?if it contains no more than one out of any three consecutive integers. How many?subsets?of? ${1,2,3,ldots,12},$ including the?empty set, are spacy?

$mathrm{(A)} 121 qquad mathrm{(B)} 123 qquad mathrm{(C)} 125 qquad mathrm{(D)} 127 qquad mathrm{(E)} 129$

2007 AMC12 A 真題答案詳細(xì)解析

$P$ ?= the amount Pam spent? $S$ ?= the amount Susan spent
$P=5 cdot (20 cdot .7) = 70$
$S=4 cdot (20 cdot .75) = 60$
Pam pays 10 more dollars than Susan? $Rightarrowfbox{C}$
The brick has volume? $8000 cm^3$ . The base of the aquarium has area? $4000 cm^2$ . For every inch the water rises, the volume increases by? $4000 cm^3$ ; therefore, when the volume increases by? $8000 cm^3$ , the water?level?rises? $2 cm Rightarrowfbox{D}$
Solution 1?Let??be the smaller term. Then?
- Thus, the answer is? $1+(1+2)=4 mathrm{(A)}$
Solution 2
- By trial and error, 1 and 3 work. 1+3=4.
$[16 cdot frac{30}{60}+4cdotfrac{90}{60}=14]$
$[frac{14}2=7Rightarrowboxed{A}]$
After paying his taxes, he has? $0.8*0.9=0.72$ ?of his earnings left. Since? $10500$ ?is? $0.28$ ?of his income, he got a total of? $frac{10500}{0.28}=37500 mathrm{(D)}$ .
Triangles? $ABC$ ?and? $ADC$ ?are?isosceles?with? $AB=BC$ ?and? $AD=DC$ . Point? $D$ ?is inside triangle? $ABC$ , angle? $ABC$ ?measures 40 degrees, and angle? $ADC$ ?measures 140 degrees. What is the degree measure of angle? $BAD$ ? $mathrm{(A)} 20qquad mathrm{(B)} 30qquad mathrm{(C)} 40qquad mathrm{(D)} 50qquad mathrm{(E)} 60$
Let??be the common difference between the terms.
- $a=c-2f$
- $b=c-f$
- $c=c$
- $d=c+f$
- $e=c+2f$
$a+b+c+d+e=5c=30$ , so? $c=6$ . But we can't find any more variables, because we don't know what? $f$ ?is. So the answer is? $textrm{C}$ .
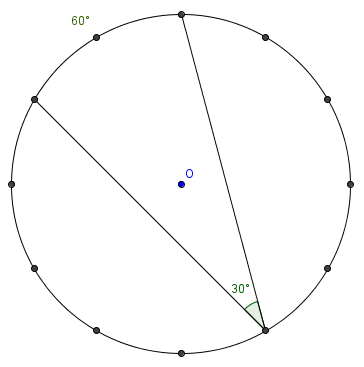We look at the angle between 12, 5, and 10. It subtends? $frac 16$ ?of the circle, or? $60$ ?degrees (or you can see that the?arc?is? $frac 23$ ?of the?right angle). Thus, the angle at each vertex is an?inscribed angle?subtending? $60$ ?degrees, making the answer? $frac 1260 = 30^{circ} Longrightarrow mathrm{(C)}$
Solution 1

Let the distance from Yan's initial position to the stadium be? $a$ ?and the distance from Yan's initial position to home be? $b$ . We are trying to find? $b/a$ , and we have the following identity given by the problem:

$begin{align*}a &= b + frac{a+b}{7}\ frac{6a}{7} &= frac{8b}{7} Longrightarrow 6a = 8bend{align*}$

Thus? $b/a = 6/8 = 3/4$ ?and the answer is? $mathrm{(B)} frac{3}{4}$

Solution 2

Another way of solving this problem is by setting the distance between Yan's home and the stadium, thus filling in one variable. Let us set the distance between the two places to be? $42z$ , where? $z$ ?is a random measurement (cause life, why not?) The distance to going to his home then riding his bike, which is? $7$ ?times faster, is equal to him just walking to the stadium. So the equation would be: Let? $x=$ ?the distance from Yan's position to his home. Let? $42z=$ ?the distance from Yan's home to the stadium.

$42-x=x+42/7$

$42-x=x+6$

$36=2x$

$x=18$

But we're still not done with the question. We know that Yan is? $18z$ ?from his home, and is? $42z-18z$ ?or? $24z$ ?from the stadium.? $18z/24z$ , the? $z$ 's cancel out, and we are left with? $3/4$ . Thus, the answer is? $mathrm{(B)} frac{3}{4}$

~ProGameXD

Solution 3

Assume that the distance from the home and stadium is 1, and the distance from Yan to home is? $b$ . Also assume that the speed of walking is 1, so the speed of biking is 7. Thus? $1-b=b+1/7$ ? $b=3/7$ ?We need? $b/1-b$

$3/7$ ?divided by? $4/7$ = $mathrm{(B)} frac{3}{4}$
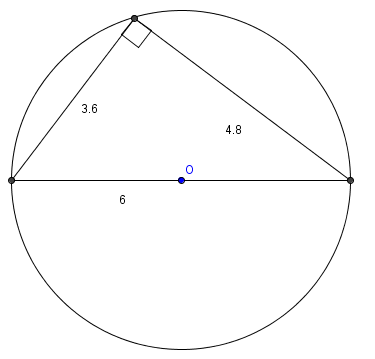Since 3-4-5 is a?Pythagorean triple, the triangle is a?right triangle. Since the hypotenuse is a?diameter?of the?circumcircle, the hypotenuse is? $2r = 6$ . Then the other legs are? $frac{24}5=4.8$ ?and? $frac{18}5=3.6$ . The area is? $frac{4.8 cdot 3.6}2 = 8.64 mathrm{(A)}$
A given digit appears?as?the hundreds digit, the tens digit, and the units digit of a term the same number of times. Let? $k$ ?be the sum of the units digits in all the terms. Then? $S=111k=3*37k$ , so? $S$ ?must be divisible by? $37 mathrm{(D)}$ . To see that it need not be divisible by any larger prime, the sequence? $123, 231, 312$ ?gives? $S=666=2 cdot 3^2 cdot 37Rightarrow mathrm{boxed{(D)}}$ .
The only times when? $ad-bc$ ?is even is when? $ad$ ?and? $bc$ ?are of the same?parity. The chance of? $ad$ ?being odd is? $frac 12 cdot frac 12 = frac 14$ , so it has a? $frac 34$ probability of being even. Therefore, the probability that? $ad-bc$ ?will be even is? $left(frac 14right)^2+left(frac 34right)^2=frac 58 mathrm{(E)}$ .
We are trying to find the foot of a?perpendicular?from? $(12,10)$ ?to? $y=-5x+18$ . Then the?slope?of the line that passes through the cheese and? $(a,b)$ ?is the negative reciprocal of the slope of the line, or? $frac 15$ . Therefore, the line is? $y=frac{1}{5}x+frac{38}{5}$ . The point where? $y=-5x+18$ ?and? $y=frac 15x+frac{38}5$ ?intersect is? $(2,8)$ , and? $2+8=10 (B)$ .
Solution 1

If 45 is expressed?as?a product of five distinct integer factors, the absolute value of the product of any four it?as?least? $|(-3)(-1)(1)(3)|=9$ , so no factor can have an absolute value greater than 5. Thus the factors of the given expression are five of the integers? $pm 3, pm 1, pm 5$ . The product of all six of these is? $-225=(-5)(45)$ , so the factors are -3, -1, 1, 3, and 5. The corresponding values of a, b, c, d, and e are 9, 7, 5, 3, and 1, and their sum is 25 (C).

Solution 2

The prime factorization of? $45$ ?is? $3^2 * 5$ . Therefore, the 5 distinct integer factors must have some negative numbers in them. Because there are two? $3$ 's in the prime factorization, one of them must be negative and the other positive. Because there is a? $-3$ , there must also be a? $-1$ ?to cancel the negatives out. The 5 distinct integer factors must be? $-3, 3, 5, -1, 1$ . The corresponding values of? $a, b, c, d,$ ?and? $e$ ?are? $9, 3, 1, 7, 5$ . and their sum is? $fbox{25 (C)}$
The median must either be??or?.?Casework:
- Median is? $6$ : Then? $n le 6$ ?and? $frac{3+6+9+10+n}{5} = 6 Longrightarrow n = 2$ .
- Median is? $9$ : Then? $n ge 9$ ?and? $frac{3+6+9+10+n}{5} = 9 Longrightarrow n = 17$ .
- Median is? $n$ : Then? $6 < n < 9$ ?and? $frac{3+6+9+10+n}{5} = n Longrightarrow n = 7$ .
All three cases are valid, so our solution is? $2 + 7 + 17 = 26 Longrightarrow mathrm{(E)}$ .
Solution 1

We can find the number of increasing?arithmetic sequences?of length 3 possible from 0 to 9, and then find all the possible permutations of these sequences.

Common difference Sequences possible Number of sequences

1 $012, ldots, 789$ 8

2 $024, ldots, 579$ 6

3 $036, ldots, 369$ 4

4 $048, ldots, 159$ 2

This gives us a total of? $2 + 4 + 6 + 8 = 20$ ?sequences. There are? $3! = 6$ ?to permute these, for a total of? $120$ .

However, we note that the conditions of the problem require three-digit numbers, and hence our numbers cannot start with zero. There are? $2! cdot 4 = 8$ ?numbers which start with zero, so our answer is? $120 - 8 = 112 Longrightarrow mathrm{(C)}$ .

Solution 2

Observe that, if the smallest and largest digit have the same parity, this uniquely determines the middle digit. If the smallest digit is not zero, then any choice of the smallest and largest digit gives? $3! = 6$ ?possible 3-digit numbers; otherwise,? $4$ ?possible 3-digit numbers. Hence we can do simple casework on whether 0 is in the number or not.

Case 1: 0 is not in the number. Then there are? $binom{5}{2} + binom{4}{2} = 16$ ?ways to choose two nonzero digits of the same parity, and each choice generates? $3! = 6$ ?3-digit numbers, giving? $16 times 6 = 96$ ?numbers.

Case 2: 0 is in the number. Then there are? $4$ ?ways to choose the largest digit (2, 4, 6, or 8), and each choice generates? $4$ ?3-digit numbers, giving? $4 times 4 = 16$ ?numbers.

Thus the total is? $96 + 16 = 112 Longrightarrow mathrm{(C)}$ .

Solution 3

This solution takes advantage of the choices available, and?as?such, will get you nowhere on the AIME and most other contests. Observe that there's a common mistake where people forget that 0 could be part of the number. 4 valid permutations of? $840,630,420,$ ?and? $210$ ?result in? $16$ total that they miss. Looking at the answers, only two differ by? $16$ , namely? $A$ ?and? $C$ . So it's safe to bet that the answer is? $mathrm{(C)}$
We can make use the of the trigonometric?Pythagorean identities: square both equations and add them up:
$sin^2 a + sin^2 b + 2sin a sin b + cos^2 a + cos^2 b + 2cos a cos b = frac{5}{3} + 1$
$2 + 2sin a sin b + 2cos a cos b = frac{8}{3}$
$2(cos a cos b + sin a sin b) = frac{2}{3}$

This is just the cosine difference identity, which simplifies to? $cos (a - b) = frac{1}{3} Longrightarrow mathrm{(B)}$
Solution 1

A fourth degree polynomial has four?roots. Since the coefficients are real(meaning that complex roots come in conjugate pairs), the remaining two roots must be the?complex conjugates?of the two given roots, namely? $2-i,-2i$ . Now we work backwards for the polynomial:

$(x-(2+i))(x-(2-i))(x-2i)(x+2i) = 0$
$(x^2 - 4x + 5)(x^2 + 4) = 0$ $x^4 - 4x^3 + 9x^2 - 16x + 20 = 0$

Thus our answer is? $- 4 + 9 - 16 + 20 = 9 mathrm{(D)}$ .

Solution 2

Just like in Solution 1 we realize that the roots come in conjugate pairs. Which means the roots are? $2i,i+2,-2i,2-i$ ?So our polynomial is

(1)? $f(x) = (x-2i)(x+2i)(x-i-2)(x-2+i)$

Looking at the equation of the polynomial? $f(x) = x^4+ax^3+bx^2+cx+d$ . We see that? $a+b+c+d = f(1)-1$

If we plug in? $1$ ?into equation?(1)?we get? $f(1) = (1-2i)(1+2i)(-1-i)(-1+i)$ .

Now if we multiply a complex number by its conjugate we get the sum of the squares of its real and imaginary parts. Using this property on the above we multiply and get? $f(1) = (1-2i)(1+2i)(-1-i)(-1+i) = (1^2+2^2)(1^2+1^2) = 10$ ?So the answer is? $f(1) -1 = 10 - 1 = 9$ .? $framebox{D}$

Common difference	Sequences possible	Number of sequences
1	$012, ldots, 789$	8
2	$024, ldots, 579$	6
3	$036, ldots, 369$	4
4	$048, ldots, 159$	2

Solution 1

From? $k = [ABC] = frac 12bh$ , we have that the height of? $triangle ABC$ ?is? $h = frac{2k}{b} = frac{2007 cdot 2}{223} = 18$ . Thus? $A$ ?lies on the lines? $y = pm 18 quad mathrm{(1)}$ .

$DE = 9sqrt{2}$ ?using 45-45-90 triangles, so in? $triangle ADE$ ?we have that? $h = frac{2 cdot 7002}{9sqrt{2}} = 778sqrt{2}$ . The slope of? $DE$ ?is? $1$ , so the equation of the line is? $y = x + b Longrightarrow b = (380) - (680) = -300 Longrightarrow y = x - 300$ . The point? $A$ ?lies on one of two?parallel?lines that are? $778sqrt{2}$ ?units away from? $overline{DE}$ . Now take an arbitrary point on the line? $overline{DE}$ ?and draw the?perpendicular?to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90? $triangle$ , so the straight line down has a length of? $778sqrt{2} cdot sqrt{2} = 1556$ . Now we note that the?y-intercept?of the parallel lines is either? $1556$ ?units above or below the y-intercept of line? $overline{DE}$ ; hence the equation of the parallel lines is? $y = x - 300 pm 1556 Longrightarrow x = y + 300 pm 1556 quad mathrm{(2)}$ .

We just need to find the intersections of these two lines and sum up the values of the?x-coordinates. Substituting the? $mathrm{(1)}$ ?into? $mathrm{(2)}$ , we get? $x = pm 18 + 300 pm 1556 = 4(300) = 1200 Longrightarrow mathrm{(E)}$ .

Solution 2

We are finding the intersection of two pairs of?parallel?lines, which will form a?parallelogram. The?centroid?of this parallelogram is just the intersection of? $overline{BC}$ ?and? $overline{DE}$ , which can easily be calculated to be? $(300,0)$ . Now the sum of the x-coordinates is just? $4(300) = 1200$ .

20.

Since the sides of a?regular polygon?are equal in length, we can call each side? $x$ . Examine one edge of the unit cube: each contains two slanted diagonal edges of an octagon and one straight edge. The diagonal edges form? $45-45-90 triangle$ ?right triangles, making the distance on the edge of the cube? $frac{x}{sqrt{2}}$ . Thus,? $2 cdot frac{x}{sqrt{2}} + x = 1$ , and? $x = frac{1}{sqrt{2} + 1} cdot left(frac{sqrt{2} - 1}{sqrt{2} - 1}right) = sqrt{2} - 1$ .

Each of the cut off corners is a?pyramid, whose volume can be calculated by? $V = frac 13 Bh$ . Use the base as one of the three?congruent?isosceles triangles, with the height being one of the edges of the pyramid that sits on the edges of the cube. The height is? $frac x{sqrt{2}} = 1 - frac{1}{sqrt{2}}$ . The base is a? $45-45-90 triangle$ ?with leg of length? $1 - frac{1}{sqrt{2}}$ , making its area? $frac 12left(1 - frac 1{sqrt{2}}right)^2 = frac{3 - 2sqrt{2}}4$ . Plugging this in, we get that the area of one of the tetrahedra is? $frac 13 left(1 - frac{1}{sqrt{2}}right)left(frac{3 - 2sqrt{2}}4right) = frac{10 - 7sqrt{2}}{24}$ . Since there are 8 removed corners, we get an answer of? $frac{10 - 7sqrt{2}}{3} Longrightarrow boxed{mathrm{B}}$

21.

By?Vieta's formulas, the sum of the roots of a?quadratic equation?is? $frac {-b}a$ , the product of the zeros is? $frac ca$ , and the sum of the coefficients is? $a + b + c$ . Setting equal the first two tells us that? $frac {-b}{a} = frac ca Rightarrow b = -c$ . Thus,? $a + b + c = a + b - b = a$ , so the common value is also equal to the coefficient of? $x^2 Longrightarrow fbox{textrm{A}}$ .

To disprove the others, note that:

$mathrm{B}$ : then? $b = frac {-b}a$ , which is not necessarily true.
$mathrm{C}$ : the y-intercept is? $c$ , so? $c = frac ca$ , not necessarily true.
$mathrm{D}$ : an x-intercept of the graph is a root of the polynomial, but this excludes the other root.
$mathrm{E}$ : the mean of the x-intercepts will be the sum of the roots of the quadratic divided by 2.

22.

Solution 1

For the sake of notation let? $T(n) = n + S(n) + S(S(n))$ . Obviously? $n<2007$ . Then the maximum value of? $S(n) + S(S(n))$ ?is when? $n = 1999$ , and the sum becomes? $28 + 10 = 38$ . So the minimum bound is? $1969$ . We do?casework?upon the tens digit:

Case 1:? $196u Longrightarrow u = 9$ . Easy to directly disprove.

Case 2:? $197u$ .? $S(n) = 1 + 9 + 7 + u = 17 + u$ , and? $S(S(n)) = 8+u$ ?if? $u le 2$ ?and? $S(S(n)) = 2 + (u-3) = u-1$ ?otherwise.

Subcase a:? $T(n) = 1970 + u + 17 + u + 8 + u = 1995 + 3u = 2007 Longrightarrow u = 4$ . This exceeds our bounds, so no solution here.

Subcase b:? $T(n) = 1970 + u + 17 + u + u - 1 = 1986 + 3u = 2007 Longrightarrow u = 7$ . First solution.

Case 3:? $198u$ .? $S(n) = 18 + u$ , and? $S(S(n)) = 9 + u$ ?if? $u le 1$ ?and? $2 + (u-2) = u$ ?otherwise.

Subcase a:? $T(n) = 1980 + u + 18 + u + 9 + u = 2007 + 3u = 2007 Longrightarrow u = 0$ . Second solution.

Subcase b:? $T(n) = 1980 + u + 18 + u + u = 1998 + 3u = 2007 Longrightarrow u = 3$ . Third solution.

Case 4:? $199u$ . But? $S(n) > 19$ , and? $n + S(n)$ ?clearly sum to? $> 2007$ .

Case 5:? $200u$ . So? $S(n) = 2 + u$ ?and? $S(S(n)) = 2 + u$ ?(recall that? $n < 2007$ ), and? $2000 + u + 2 + u + 2 + u = 2004 + 3u = 2007 Longrightarrow u = 1$ . Fourth solution.

In total we have? $4 mathrm{(D)}$ ?solutions, which are? $1977, 1980, 1983,$ ?and? $2001$ .

Solution 2

Clearly,? $n > 1950$ . We can break this into three cases:

Case 1:? $n geq 2000$

Inspection gives? $n = 2001$ .

Case 2:? $n < 2000$ ,? $n = 19xy$ ?(not to be confused with? $19*x*y$ ),? $x + y < 10$

If you set up an equation, it reduces to

$4x + y = 32$

which has as its only solution satisfying the constraints? $x = 8$ ,? $y = 0$ .

Case 3:? $n < 2000$ ,? $n = 19xy$ ,? $x + y geq 10$

This reduces to

$4x + y = 35$ . The only two solutions satisfying the constraints for this equation are? $x = 7$ ,? $y = 7$ ?and? $x = 8$ ,? $y = 3$ .

The solutions are thus? $1977, 1980, 1983, 2001$ ?and the answer is? $mathrm{(D)} 4$ .

Solution 3

As?in Solution 1, we note that? $S(n)leq 28$ ?and? $S(S(n))leq 10$ .
Obviously,? $nequiv S(n)equiv S(S(n)) pmod 9$ .
As? $2007equiv 0 pmod 9$ , this means that? $nbmod 9 in{0,3,6}$ , or equivalently that? $nequiv S(n)equiv S(S(n))equiv 0 pmod 3$ .

Thus? $S(S(n))in{3,6,9}$ . For each possible? $S(S(n))$ ?we get three possible? $S(n)$ .
(E. g., if? $S(S(n))=6$ , then? $S(n)=x$ ?is a number such that? $xleq 28$ ?and? $S(x)=6$ , therefore? $S(n)in{6,15,24}$ .)

For each of these nine possibilities we compute? $n_{?}$ ?as? $2007-S(n)-S(S(n))$ ?and check whether? $S(n_{?})=S(n)$ .
We'll find out that out of the 9 cases, in 4 the value? $n_{?}$ ?has the correct sum of digits.
This happens for? $n_{?}in { 1977, 1980, 1983, 2001 }$ .

Solution 4

This solution is not a good solution, but is viable for in contest situations

Clearly? $nequiv S(n) pmod 9$ . Thus, $[n+S(n)+S(S(n))equiv 0 pmod 9 implies nequiv 0pmod 3.]$ Now we need a bound for? $n$ . It is clear that the maximum for? $S(n)=36$ ?(from? $n=9999$ ) which means the maximum for? $S(n)+S(S(n))$ ?is? $45$ . This means that? $ngeq 1962$ .

Warning: This is where you will cringe badly

Now check all multiples of? $3$ ?from? $1962$ ?to? $2007$ ?and we find that only? $n=1977, 1980, 1983, 2001$ ?work, so our answer is? $mathrm{(D)} 4$ .

Remark: this may seem time consuming, but in reality, calculating? $n+S(n)+S(S(n))$ ?for? $16$ ?values is actually very quick, so this solution would only take approximately 3-5 minutes, helpful in a contest.

23.

Let? $x$ ?be the x-coordinate of? $B$ ?and? $C$ , and? $x_2$ ?be the x-coordinate of? $A$ ?and? $y$ ?be the y-coordinate of? $A$ ?and? $B$ . Then? $2log_ax= y Longrightarrow a^{y/2} = x$ and? $log_ax_2 = y Longrightarrow x_2 = a^y = left(a^{y/2}right)^2 = x^2$ . Since the distance between? $A$ ?and? $B$ ?is? $6$ , we have? $x^2 - x - 6 = 0$ , yielding? $x = -2, 3$ .

However, we can discard the negative root (all three?logarithmic?equations are underneath the line? $y = 3$ ?and above? $y = 0$ ?when? $x$ ?is negative, hence we can't squeeze in a square of side 6). Thus? $x = 3$ .

Substituting back,? $3log_{a}x - 2log_{a}x = 6 Longrightarrow a^6 = x$ , so? $a = sqrt[6]{3} mathrm{(A)}$ .

24.

Solution 1

$F(2)=3$

By looking at various graphs, we obtain that, for most of the graphs

$F(n) = n + 1$

Notice that the solutions are basically reflections across? $x = frac{pi}{2}$ . However, when? $n equiv 1 pmod{4}$ , the middle apex of the?sine?curve touches the sine curve at the top only one time (instead of two reflected points), so we get here? $2007 AMC12A 真題及答案詳細(xì)解析$ .

$3+4+5+5+7+8+9+9+cdots+2008$ ? $= (1+2+3+4+5+cdots+2008) - 3 - 501$ ? $= frac{(2008)(2009)}{2} - 504 = 2016532$ $mathrm{(D)}$

Solution 2

$[sin nx - sin x = 2left( cos frac {n + 1}{2}xright) left( sin frac {n - 1}{2}xright)]$ So? $sin nx = sin x$ ?if and only if? $cos frac {n + 1}{2}x = 0$ ?or? $sin frac {n - 1}{2}x = 0$ .

The first occurs whenever? $frac {n + 1}{2}x = (j + 1/2)pi$ , or? $x = frac {(2j + 1)pi}{n + 1}$ ?for some nonnegative integer? $j$ . Since? $xleq pi$ ,? $jleq n/2$ . So there are? $1 + lfloor n/2 rfloor$ ?solutions in this case.

The second occurs whenever? $frac {n - 1}{2}x = kpi$ , or? $x = frac {2kpi}{n - 1}$ ?for some nonnegative integer? $k$ . Here? $kleq frac {n - 1}{2}$ ?so that there are? $leftlfloor frac {n + 1}{2}rightrfloor$ solutions here.

However, we overcount intersections. These occur whenever $[frac {2j + 1}{n + 1} = frac {2k}{n - 1}]$

$[k = frac {(2j + 1)(n - 1)}{2(n + 1)}]$ which is equivalent to? $2(n + 1)$ ?dividing? $(2j + 1)(n - 1)$ . If? $n$ ?is even, then? $(2j + 1)(n - 1)$ ?is odd, so this never happens. If? $nequiv 3pmod{4}$ , then there won't be intersections either, since a multiple of 8 can't divide a number which is not even a multiple of 4.

This leaves? $nequiv 1pmod{4}$ . In this case, the divisibility becomes? $frac {n + 1}{2}$ ?dividing? $(2j + 1)frac {n - 1}{4}$ . Since? $frac {n + 1}{2}$ ?and? $frac {n - 1}{4}$ ?are relatively prime (subtracting twice the second number from the first gives 1),? $frac {n + 1}{2}$ ?must divide? $2j + 1$ . Since? $jleq frac {n - 1}{2}$ ,? $2j + 1leq n < 2cdot frac {n + 1}{2}$ . Then there is only one intersection, namely when? $j = frac {n - 1}{4}$ .

Therefore we find? $F(n)$ ?is equal to? $1 + lfloor n/2 rfloor + left lfloor frac {n + 1}{2}rightrfloor = n + 1$ , unless? $nequiv 1pmod{4}$ , in which case it is one less, or? $n$ . The problem may then be finished?as?in Solution 1.

25.

Solution 1

Let? $S_{n}$ ?denote the number of spacy subsets of? ${ 1, 2, ... n }$ . We have? $S_{0} = 1, S_{1} = 2, S_{2} = 3$ .

The spacy subsets of? $S_{n + 1}$ ?can be divided into two groups:

$A =$ ?those not containing? $n + 1$ . Clearly? $|A|=S_{n}$ .
$B =$ ?those containing? $n + 1$ . We have? $|B|=S_{n - 2}$ , since removing? $n + 1$ ?from any set in? $B$ ?produces a spacy set with all elements at most equal to? $n - 2,$ ?and each such spacy set can be constructed from exactly one spacy set in? $B$ .

Hence,

$S_{n + 1} = S_{n} + S_{n - 2}$

From this?recursion, we find that

$S(0)$	$S(1)$	$S(2)$	$S(3)$	$S(4)$	$S(5)$	$S(6)$	$S(7)$	$S(8)$	$S(9)$	$S(10)$	$S(11)$	$S(12)$
1	2	3	4	6	9	13	19	28	41	60	88	129

And so the answer is? $E$ ,? $129$ .

Solution 2

Since each of the elements of the subsets must be spaced at least two apart, a divider counting argument can be used.

From the set? ${1,2,3,4,5,6,7,8,9,10,11,12}$ ?we choose at most four numbers. Let those numbers be represented by balls. Between each of the balls there are at least two dividers. So for example, o | | o | | o | | o | | represents? ${1,4,7,10}$ .

For subsets of size? $k$ ?there must be? $2(k - 1)$ ?dividers between the balls, leaving? $12 - k - 2(k - 1) = 12 - 3k + 2$ ?dividers to be be placed in? $k + 1$ ?spots between the balls. The number of way this can be done is? $binom{(12 - 3k + 2) + (k + 1) - 1}k = binom{12 - 2k + 2}k$ .

Therefore, the number of spacy subsets is? $binom 64 + binom 83 + binom{10}2 + binom{12}1 + binom{14}0 = 129$ .

Solution 3

A shifting argument is also possible, and is similar in spirit to Solution 2. Clearly we can have at most? $4$ ?elements. Given any arrangment, we subract? $2i-2$ ?from the? $i-th$ ?element in our subset, when the elements are arranged in increasing order. This creates a?bijection?with the number of size? $k$ ?subsets of the set of the first? $14-2k$ ?positive integers. For instance, the arrangment o | | o | | o | | | o | corresponds to the arrangment o o o | o |. Notice that there is no longer any restriction on consectutive numbers. Therefore, we can easily plug in the possible integers 0, 1, 2, 3, 4, 5 for? $k$ :? ${14 choose 0} + {12 choose 1} + {10 choose 2} + {8 choose 3} + {6 choose 4} = boxed{129}$

In general, the number of subsets of a set with? $n$ ?elements and with no? $k$ ?consecutive numbers is? $sum^{lfloor{frac{n}{k}}rfloor}_{i=0}{{n-(k-1)(i-1) choose i}}$ .