Home » 國際競賽 » 數學國際競賽 » AMC美國數學競賽 » Details

2003 AMC12B 真題及答案詳細解析

Category: AMC美國數學競賽, 國際競賽 Date: 2019年12月5日上午11:16

2003 AMC 12 B 真題

答案詳細解析請參考文末

Problem 1

Which of the following is the same?as

$[frac{2-4+6-8+10-12+14}{3-6+9-12+15-18+21}?]$

$text {(A) } -1 qquad text {(B) } -frac{2}{3} qquad text {(C) } frac{2}{3} qquad text {(D) } 1 qquad text {(E) } frac{14}{3}$

Problem 2

Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs 1 dollar more than a pink pill, and Al's pills cost a total of 546 dollars for the two weeks. How much does one green pill cost?

$text {(A) } 7 qquad text {(B) } 14 qquad text {(C) } 19 qquad text {(D) } 20 qquad text {(E) } 39$

Problem 3

Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are?as?shown in the figure. She plants one flower per square foot in each region. Asters cost $1 each, begonias $1.50 each, cannas $2 each, dahlias $2.50 each, and Easter lilies $3 each. What is the least possible cost, in dollars, for her garden?

Problem 3.png

$text {(A) } 108 qquad text {(B) } 115 qquad text {(C) } 132 qquad text {(D) } 144 qquad text {(E) } 156$

Problem 4

Moe uses a mower to cut his rectangular 90-foot by 150-foot lawn. The swath he cuts is 28 inches wide, but he overlaps each cut by 4 inches to make sure that no grass is missed. he walks at the rate of 5000 feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?

$text {(A) } 0.75 qquad text {(B) } 0.8 qquad text {(C) } 1.35 qquad text {(D) } 1.5 qquad text {(E) } 3$

Problem 5

Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is 4?: 3. The horizontal length of a "27-inch" television screen is closest, in inches, to which of the following?

Problem 5.PNG

$text {(A) } 20 qquad text {(B) } 20.5 qquad text {(C) } 21 qquad text {(D) } 21.5 qquad text {(E) } 22$

Problem 6

The second and fourth terms of a geometric sequence are 2 and 6. Which of the following is a possible first term?

$text {(A) } -sqrt{3} qquad text {(B) } frac{-2sqrt{3}}{3} qquad text {(C) } frac{-sqrt{3}}{3} qquad text {(D) } sqrt{3} qquad text {(E) } 3$

Problem 7

Penniless Pete's piggy bank has no pennies in it, but it has 100 coins, all nickels,dimes, and quarters, whose total value is $8.35. It does not necessarily contain coins of all three types. What is the difference between the largest and smallest number of dimes that could be in the bank?

$text {(A) } 0 qquad text {(B) } 13 qquad text {(C) } 37 qquad text {(D) } 64 qquad text {(E) } 83$

Problem 8

Let? $clubsuit(x)$ ?denote the sum of the digits of the positive integer? $x$ . For example,? $clubsuit(8) = 8$ ?and? $clubsuit(123) = 1 + 2 + 3 = 6.$ ?For how many two-digit values of? $x$ ?is? $clubsuit(clubsuit(x)) = 3?$

$text{(A) }3qquadtext{(B) }4qquadtext{(C) }6qquadtext{(D) }9qquadtext{(E) }10$

Problem 9

Let? $f$ ?be a linear function for which? $f(6) - f(2) = 12.$ ?What is? $f(12) - f(2)?$

$text {(A) } 12 qquad text {(B) } 18 qquad text {(C) } 24 qquad text {(D) } 30 qquad text {(E) } 36$

Problem 10

Several figures can be made by attaching two equilateral triangles to the regular pentagon ABCDE in two of the five positions shown. How many non-congruent figures can be constructed in this way?

$[asy] size(200); defaultpen(0.9); real r = 5/dir(54).x, h = 5 tan(54*pi/180); pair A = (5,0), B = A+10*dir(72), C = (0,r+h), E = (-5,0), D = E+10*dir(108); draw(A--B--C--D--E--cycle); label("(A)",A+(0,-0.5),SSE); label("(B)",B+(0.5,0),ENE); label("(C)",C+(0,0.5),N); label("(D)",D+(-0.5,0),WNW); label("(E)",E+(0,-0.5),SW); // real l = 5*sqrt(3); pair ab = (h+l)*dir(72), bc = (h+l)*dir(54); pair AB = (ab.y, h-ab.x), BC = (bc.x,h+bc.y), CD = (-bc.x,h+bc.y), DE = (-ab.y, h-ab.x), EA = (0,-l); draw(A--AB--B^^B--BC--C^^C--CD--D^^D--DE--E^^E--EA--A, dashed); // dot(A); dot(B); dot(C); dot(D); dot(E); dot(AB); dot(BC); dot(CD); dot(DE); dot(EA); [/asy]$ $text {(A) } 1 qquad text {(B) } 2 qquad text {(C) } 3 qquad text {(D) } 4 qquad text {(E) } 5$

Problem 11

Cassandra sets her watch to the correct time at noon. At the actual time of 1:00 PM, she notices that her watch reads 12:57 and 36 seconds. Assuming that her watch loses time at a constant rate, what will be the actual time when her watch first reads 10:00 PM?

$text {(A) 10:22 PM and 24 seconds} qquad text {(B) 10:24 PM} qquad text {(C) 10:25 PM} qquad text {(D) 10:27 PM} qquad text {(E) 10:30 PM}$

Problem 12

What is the largest integer that is a divisor of? $(n+1)(n+3)(n+5)(n+7)(n+9)$ ?for all positive even integers? $n$ ?

$text {(A) } 3 qquad text {(B) } 5 qquad text {(C) } 11 qquad text {(D) } 15 qquad text {(E) } 165$

Problem 13

An ice cream?cone?consists of a?sphere?of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly fill the cone. Assume that the melted ice cream occupies? $75%$ ?of the volume of the frozen ice cream. What is the ratio of the cone’s height to its?radius?

$mathrm{(A)} 2:1 qquadmathrm{(B)} 3:1 qquadmathrm{(C)} 4:1 qquadmathrm{(D)} 16:3 qquadmathrm{(E)} 6:1$

Problem 14

In rectangle ABCD, AB = 5 and BC = 3. Points F and G are on CD so that DF = 1 and GC = 2. Lines AF and BG intersect at E. Find the area of? $triangle{AEB}$ .? Problem 14.png

$text {(A) } 10 qquad text {(B) } frac{21}{2} qquad text {(C) } 12 qquad text {(D) } frac{25}{2} qquad text {(E) } 15$

Problem 15

A regular octagon? $ABCDEFGH$ ?has an area of one square unit. What is the area of the rectangle? $ABEF$ ?

Problem 15.PNG

$text {(A) } 1-frac{sqrt{2}}{2} qquad text {(B) } frac{sqrt{2}}{4} qquad text {(C) } sqrt{2}-1 qquad text {(D) } frac{1}{2} qquad text {(E) } frac{1+sqrt{2}}{4}$

Problem 16

Three semicircles of radius 1 are constructed on diameter AB of a semicircle of radius 2. The centers of the small semicircles divide AB into four line segments of equal length,?as?shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?

$[asy] import graph; unitsize(14mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); dashed=linetype("4 4"); dotfactor=3; pair A=(-2,0), B=(2,0); fill(Arc((0,0),2,0,180)--cycle,mediumgray); fill(Arc((-1,0),1,0,180)--cycle,white); fill(Arc((0,0),1,0,180)--cycle,white); fill(Arc((1,0),1,0,180)--cycle,white); draw(Arc((-1,0),1,60,180)); draw(Arc((0,0),1,0,60),dashed); draw(Arc((0,0),1,60,120)); draw(Arc((0,0),1,120,180),dashed); draw(Arc((1,0),1,0,120)); draw(Arc((0,0),2,0,180)--cycle); dot((0,0)); dot((-1,0)); dot((1,0)); draw((-2,-0.1)--(-2,-0.3),gray); draw((-1,-0.1)--(-1,-0.3),gray); draw((1,-0.1)--(1,-0.3),gray); draw((2,-0.1)--(2,-0.3),gray); label("$A$",A,W); label("$B$",B,E); label("1",(-1.5,-0.1),S); label("2",(0,-0.1),S); label("1",(1.5,-0.1),S);[/asy]$

$textbf{(A) } pi - sqrt{3} qquadtextbf{(B) } pi - sqrt{2} qquadtextbf{(C) } frac{pi + sqrt{2}}{2} qquadtextbf{(D) } frac{pi +sqrt{3}}{2} qquadtextbf{(E) } frac{7}{6}pi - frac{sqrt{3}}{2}$

Problem 17

If? $log (xy^3) = 1$ ?and? $log (x^2y) = 1$ , what is? $log (xy)$ ?

$mathrm{(A)} -frac 12 qquadmathrm{(B)} 0 qquadmathrm{(C)} frac 12 qquadmathrm{(D)} frac 35 qquadmathrm{(E)} 1$

Problem 18

Let? $x$ ?and? $y$ ?be positive integers such that? $7x^5 = 11y^{13}.$ ?The minimum possible value of? $x$ ?has a prime factorization? $a^cb^d.$ ?What is? $a + b + c + d$ ?

$textbf{(A)} 30 qquad textbf{(B)} 31 qquad textbf{(C)} 32 qquad textbf{(D)} 33 qquad textbf{(E)} 34$

Problem 19

Let? $S$ ?be the?set?of?permutations?of the?sequence? $1,2,3,4,5$ ?for which the first term is not? $1$ . A permutation is chosen randomly from? $S$ . The?probability?that the second term is? $2$ , in lowest terms, is? $a/b$ . What is? $a+b$ ?

$mathrm{(A)} 5 qquadmathrm{(B)} 6 qquadmathrm{(C)} 11 qquadmathrm{(D)} 16 qquadmathrm{(E)} 19$

Problem 20

Part of the graph of? $f(x) = ax^3 + bx^2 + cx + d$ ?is shown. What is? $b$ ?

2003 12B AMC-20.png

$mathrm{(A)} -4 qquadmathrm{(B)} -2 qquadmathrm{(C)} 0 qquadmathrm{(D)} 2 qquadmathrm{(E)} 4$

Problem 21

An object moves? $8$ ?cm in a straight?line?from? $A$ ?to? $B$ , turns at an angle? $alpha$ , measured in radians and chosen at random from the interval? $(0,pi)$ , and moves? $5$ ?cm in a straight line to? $C$ . What is the?probability?that? $AC < 7$ ?

$mathrm{(A)} frac{1}{6} qquadmathrm{(B)} frac{1}{5} qquadmathrm{(C)} frac{1}{4} qquadmathrm{(D)} frac{1}{3} qquadmathrm{(E)} frac{1}{2}$

Problem 22

Let? $ABCD$ ?be a?rhombus?with? $AC = 16$ ?and? $BD = 30$ . Let? $N$ ?be a point on? $overline{AB}$ , and let? $P$ ?and? $Q$ ?be the feet of the perpendiculars from? $N$ to? $overline{AC}$ ?and? $overline{BD}$ , respectively. Which of the following is closest to the minimum possible value of? $PQ$ ?

$[asy] size(200); defaultpen(0.6); pair O = (15*15/17,8*15/17), C = (17,0), D = (0,0), P = (25.6,19.2), Q = (25.6, 18.5); pair A = 2*O-C, B = 2*O-D; pair P = (A+O)/2, Q=(B+O)/2, N=(A+B)/2; draw(A--B--C--D--cycle); draw(A--O--B--O--C--O--D); draw(P--N--Q); label("(A)",A,WNW); label("(B)",B,ESE); label("(C)",C,ESE); label("(D)",D,SW); label("(P)",P,SSW); label("(Q)",Q,SSE); label("(N)",N,NNE); [/asy]$ $mathrm{(A)} 6.5 qquadmathrm{(B)} 6.75 qquadmathrm{(C)} 7 qquadmathrm{(D)} 7.25 qquadmathrm{(E)} 7.5$

Problem 23

The number of? $x$ -intercepts on the graph of? $y=sin(1/x)$ ?in the interval? $(0.0001,0.001)$ ?is closest to

$mathrm{(A)} 2900 qquadmathrm{(B)} 3000 qquadmathrm{(C)} 3100 qquadmathrm{(D)} 3200 qquadmathrm{(E)} 3300$

Problem 24

Positive integers? $a,b,$ ?and? $c$ ?are chosen so that? $a<b<c$ , and the system of?equations

$2x + y = 2003 quad$ ?and? $quad y = |x-a| + |x-b| + |x-c|$ has exactly one solution. What is the minimum value of? $c$ ?

$mathrm{(A)} 668 qquadmathrm{(B)} 669 qquadmathrm{(C)} 1002 qquadmathrm{(D)} 2003 qquadmathrm{(E)} 2004$

Problem 25

Three points are chosen randomly and independently on a circle. What is the probability that all three pairwise distance between the points are less than the radius of the circle?

$mathrm{(A)} dfrac{1}{36} qquadmathrm{(B)} dfrac{1}{24} qquadmathrm{(C)} dfrac{1}{18} qquadmathrm{(D)} dfrac{1}{12} qquadmathrm{(E)} dfrac{1}{9}$

2003 AMC12 B 真題答案詳細解析

The numbers in the numerator and denominator can be grouped like this:
$begin{align*} 2+(-4+6)+(-8+10)+(-12+14)&=2*4\ 3+(-6+9)+(-12+15)+(-18+21)&=3*4\ frac{2*4}{3*4}&=frac{2}{3} Rightarrow text {(C)} end{align*}$
Alternatively, notice that each term in the numerator is? $frac{2}{3}$ ?of a term in the denominator, so the quotient has to be? $frac{2}{3}$ .
Because there are? $14$ ?days in two weeks, Al spends? $546/14 = 39$ ?dollars per day for the cost of a green pill and a pink pill. If the green pill costs? $x$ ?dollars and the pink pill? $x-1$ ?dollars, the sum of the two costs? $2x-1$ ?should equal? $39$ ?dollars. Then the cost of the green pill? $x$ ?is? $boxed{textbf{(D) }textdollar 20}$ .
The areas of the five regions from greatest to least are? $21,20,15,6$ ?and? $4$ .If we want to minimize the cost, we want to maximize the area of the cheapest flower and minimize the area of the most expensive flower. Doing this, the cost is? $1cdot21+1.50cdot20+2cdot15+2.50cdot6+3cdot4$ , which simplifies to? $$$$ $108$ . Therefore the answer is? $boxed{textbf{(A) } 108}$ .
Since the swath Moe actually mows is? $24$ ?inches, or? $2$ ?feet wide, he mows? $10000$ ?square feet in one hour. His lawn has an area of? $13500$ , so it will take Moe? $1.35$ ?hours to finish mowing the lawn. Thus the answer is? $boxed{textbf{(C) } 1.35}$ .
Solution 1

If you divide the television screen into two right triangles, the legs are in the ratio of? $4?: 3$ , and we can let one leg be? $4x$ ?and the other be? $3x$ . Then we can use the Pythagorean Theorem.

$begin{align*}(4x)^2+(3x)^2&=27^2\ 16x^2+9x^2&=729\ 25x^2&=729\ x^2&=frac{729}{25}\ x&=frac{27}{5}\ x&=5.4end{align*}$

The horizontal length is? $5.4times4=21.6$ , which is closest to? $boxed{textbf{(D) } 21.5}$ .

Solution 2

One can realize that the diagonal, vertical, and horizontal lengths all make up a? $3,4,5$ ?triangle. Therefore, the horizontal length, being the? $4$ ?in the? $4?: 3$ ?ratio, is simply? $frac{4}{5}$ ?times the hypotenuse.? $frac{4}{5}cdot27=21.6 approx boxed{textbf{(D) } 21.5}$ .
Let the first term be? $a$ ?and the common difference be? $r$ . Therefore, $[ar=2 (1) qquad text{and} qquad ar^3=6 (2)]$ Dividing? $(2)$ ?by? $(1)$ ?eliminates the? $a$ , yielding? $r^2=3$ , so? $r=pmsqrt{3}$ .Now, since? $ar=2$ ,? $a=frac{2}{r}$ , so? $a=frac{2}{pmsqrt{3}}=pmfrac{2sqrt{3}}{3}$ .We therefore see that? $boxed{textbf{(B)} -frac{2sqrt{3}}{3}}$ ?is a possible first term.
Where? $a,b,c$ ?is the number of nickels, dimes, and quarters, respectively, we can set up two equations: $[(1) 5a+10b+25c=835 (2) a+b+c=100]$ Eliminate? $a$ ?by subtracting? $(2)$ ?from? $(1)/5$ ?to get? $b+4c=67$ . Of the integer solutions? $(b,c)$ ?to this equation, the number of dimes? $b$ ?is least in? $(3,16)$ ?and greatest in? $(67,0)$ , yielding a difference of? $67-3=boxed{textbf{(D)} 64}$ .
Let? $a$ ?and? $b$ ?be the digits of? $clubsuit(x)$ , $[clubsuit(clubsuit(x)) = a + b = 3]$ Clearly? $clubsuit(x)$ ?can only be? $3, 12, 21,$ ?or? $30$ ?and only? $3$ ?and? $12$ ?are possible to have two digits sum to.If? $clubsuit(x)$ ?sums to? $3$ , there are 3 different solutions?:? $12, 21, text{or } 30$ If? $clubsuit(x)$ ?sums to? $12$ , there are 7 different solutions:? $39, 48, 57, 66,75, 84, text{or } 93$ The total number of solutions is? $3 + 7 =10 Rightarrow text (E)$
Since? $f$ ?is a linear function with slope? $m$ , $[m = frac{f(6) - f(2)}{Delta x} = frac{12}{6 - 2} = 3]$ $[f(12) - f(2) = m Delta x = 3(12 - 2) = 30 Rightarrow text (D)]$
Place the first triangle. Now, we can place the second triangle either adjacent to the first, or with one side between them, for a total of? $boxed{text{(B) }2}$

Solution 2

Take? ${5 choose 2}$ ?to realize there are 10 ways to choose 2 different triangles. Then divide by 5 for each vertice of a pentagon to get? $boxed{text{(B) }2}$
For every? $60$ ?minutes that pass by in actual time,? $57+frac{36}{60}=57.6$ ?minutes pass by on Cassandra's watch. When her watch first reads, 10:00 pm,? $10(60)=600$ ?minutes have passed by on her watch. Setting up a proportion, $[frac{57.6}{60}=frac{600}{x}]$ where? $x$ ?is the number of minutes tha
For all consecutive odd integers, one of every five is a multiple of 5 and one of every three is a multiple of 3. The answer is? $3 cdot 5 = 15$ , so ${boxed{textbf{(D)15}}}$ ?is the correct answer.
Let? $r$ ?be the common radius of the sphere and the cone, and? $h$ ?be the cone’s height. Then $[75% cdot left(frac 43 pi r^3right) = frac 13 pi r^2 h Longrightarrow h = 3r]$ Thus? $h:r = 3:1$ ?and the answer is? $boxed{B}$ .
Solution 1

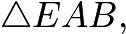
$triangle EFG sim triangle EAB$ ?because? $FG parallel AB.$ ?The ratio of? $triangle EFG$ ?to? $triangle EAB$ ?is? $2:5$ ?since? $AB=5$ ?and? $FG=2$ ?from subtraction. If we let? $h$ be the height of? $triangle EAB,$

$[frac{2}{5} = frac{h-3}{h}]$ $[2h = 5h-15]$ $[3h = 15]$ $[h = 5]$

The height is? $5$ ?so the area of? $triangle EAB$ ?is? $frac{1}{2}(5)(5) = boxed{textbf{(D)} frac{25}{2}}$ .

Solution 2

We can look at this diagram?as?if it were a coordinate plane with point? $A$ ?being? $(0,0)$ . This means that the equation of the line? $AE$ ?is? $y=3x$ and the equation of the line? $EB$ ?is? $y=frac{-3}{2}x+frac{15}{2}$ . From this we can set of the follow equation to find the? $x$ ?coordinate of point? $E$ :

$[3x=frac{-3}{2}x+frac{15}{2}]$ $[6x=-3x+15]$ $[9x=15]$ $[x=frac{5}{3}]$

We can plug this into one of our original equations to find that the? $y$ ?coordinate is? $5$ , meaning the area of? $triangle EAB$ ?is? $frac{1}{2}(5)(5) = boxed{textbf{(D)} frac{25}{2}}$

Solution 3

At points? $A$ ?and? $B$ , segment? $AE$ ?is 5 units from segment? $BE$ . At points? $F$ ?and? $G$ , the segments are 2 units from each other. This means that collectively, the two lines closed the distance between them by 3 units over a height of 3 units. Therefore, to close the next two units of distance, they will have to travel a height of 2 units.

Then calculate the area of trapezoid? $FGBA$ ?and triangle? $EGF$ ?separately and add them. The area of the trapezoid is? $frac {2+5}{2}cdot 3 = frac {21}{2}$ ?and the area of the triangle is? $frac{1}{2}cdot 2 cdot 2 = 2$ .? $frac{21}{2}+2=boxed{textbf{(D)} frac{25}{2}}$
Solution 1

Here is an easy way to look at this, where? $p$ ?is the perimeter, and? $a$ ?is the?apothem:

Area of Octagon:? $frac{ap}{2}=1$ .

Area of Rectangle:? $frac{p}{8}times 2a=frac{ap}{4}$ .

You can see from this that the octagon's area is twice?as?large?as?the rectangle's area is? $boxed{textbf{(D)} frac{1}{2}}$ .

Solution 2

$[asy] unitsize(1cm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair C=dir(22.5), B=dir(67.5), A=dir(112.5), H=dir(157.5), G=dir(202.5), F=dir(247.5), E=dir(292.5), D=dir(337.5); draw(A--B--C--D--E--F--G--H--cycle); label("$A$",A,NNW); label("$B$",B,NNE); label("$C$",C,ENE); label("$D$",D,ESE); label("$E$",E,SSE); label("$F$",F,SSW); label("$G$",G,WSW); label("$H$",H,WNW); draw(A--E--F--B--C--G--H--D); draw(A--E--F--B--A,blue); draw(A--F--E--B--A,red); [/asy]$

Here is a less complicated way than that of the user above. If you draw a line segment from each vertex to the center of the octagon and draw the rectangle ABEF( In red), you can see that two of the triangles (In blue) share the same base and height with half the rectangle. Therefore, the rectangle's area is the same as 4 of the 8 triangles, and is? $boxed{textbf{(D)} frac{1}{2}}$ ?the area of the octagon.

Solution 3

$[asy] unitsize(1cm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair C=dir(22.5), B=dir(67.5), A=dir(112.5), H=dir(157.5), G=dir(202.5), F=dir(247.5), E=dir(292.5), D=dir(337.5); draw(A--B--C--D--E--F--G--H--cycle); label("$A$",A,NNW); label("$B$",B,NNE); label("$C$",C,ENE); label("$D$",D,ESE); label("$E$",E,SSE); label("$F$",F,SSW); label("$G$",G,WSW); label("$H$",H,WNW); draw(A--D--E--H--G--B--C--F); [/asy]$ Drawing lines? $AD$ ,? $BG$ ,? $CF$ , and? $EH$ , we can see that the octagon is comprised of? $1$ ?square,? $4$ ?rectangles, and? $4$ ?triangles. The triangles each are? $45-45-90$ ?triangles, and since their diagonal is length? $x$ , each of their sides is? $frac{sqrt{2}}{2}x$ . The area of the entire figure is, likewise,? $x^2$ ?(the square) $+4x^2frac{sqrt{2}}{2}$ ?(the 4 rectangles) $+2cdot(frac{sqrt{2}}{2}x)^2$ ?(the triangles), which simplifies to? $2x^2 + 2sqrt{2}x^2$ . The area of? $ABEF$ ?is just? $x(x+frac{2sqrt{2}}{2}x)$ , or? $x^2$ ?+? $x^2sqrt{2}$ , which we can see is the area of? $frac{ABCDEFGH}{2} = boxed{textbf{(D)} frac{1}{2}}$ ?the area of the octagon.
$[asy] import graph; unitsize(14mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); dashed=linetype("4 4"); dotfactor=3; pair A=(-2,0), B=(2,0); fill(Arc((0,0),2,0,180)--cycle,mediumgray); fill(Arc((-1,0),1,0,180)--cycle,white); fill(Arc((0,0),1,0,180)--cycle,white); fill(Arc((1,0),1,0,180)--cycle,white); draw(Arc((-1,0),1,60,180)); draw(Arc((0,0),1,0,60),dashed); draw(Arc((0,0),1,60,120)); draw(Arc((0,0),1,120,180),dashed); draw(Arc((1,0),1,0,120)); draw(Arc((0,0),2,0,180)--cycle); dot((0,0)); dot((-1,0)); dot((1,0)); draw((-2,-0.1)--(-2,-0.3),gray); draw((-1,-0.1)--(-1,-0.3),gray); draw((1,-0.1)--(1,-0.3),gray); draw((2,-0.1)--(2,-0.3),gray); label("$A$",A,W); label("$B$",B,E); label("1",(-1.5,-0.1),S); label("2",(0,-0.1),S); label("1",(1.5,-0.1),S); draw((1,0)--(0.5,0.866)); draw((0,0)--(0.5,0.866)); draw((-1,0)--(-0.5,0.866)); draw((0,0)--(-0.5,0.866));[/asy]$ By drawing four lines from the intersect of the semicircles to their centers, we have split the white region into? $frac{5}{6}$ ?of a circle with radius? $1$ ?and two equilateral triangles with side length? $1$ . This gives the area of the white region?as? $frac{5}{6}pi+frac{2cdotsqrt3}{4}=frac{5}{6}pi+frac{sqrt3}{2}$ . The area of the shaded region is the area of the white region subtracted from the area of the large semicircle. This is equivalent to? $2pi-left(frac{5}{6}pi+frac{sqrt3}{2}right)=frac{7}{6}pi-frac{sqrt3}{2}$ .Thus the answer is? $boxed{textbf{(E)} frac{7}{6}pi-frac{sqrt3}{2}}$ .
Since $begin{align*} &log(xy) +2log y = 1 \ log(xy) + log x = 1 quad Longrightarrow quad &2log(xy) + 2log x = 2 end{align*}$ Summing gives $[3log(xy) + 2log y + 2log x = 3 Longrightarrow 5log(xy) = 3]$ Hence? $log (xy) = frac 35 Rightarrow mathrm{(D)}$ .It is not difficult to find? $x = 10^{frac{2}{5}}, y = 10^{frac{1}{5}}$ .

Solution 2

$log(xy)+log(y^2)=1 \ log(xy)+log(x)=1 text{ subtracting, } \ log(y^2)-log(x)=0 \ log left(frac{y^2}{x}right)=0 \ frac{y^2}{x}=10^0 \ y^2=x \ text{substitute and solve: } log(y^5)=5log(y)=1 \ text{ and we need } 3log(y) text{ which is } frac{3}{5}$
Solution 1

Substitute? $a^cb^d$ ?into? $x$ . We then have? $7(a^{5c}b^{5d}) = 11y^{13}$ . Divide both sides by? $7$ , and it follows that:

$[(a^{5c}b^{5d}) = frac{11y^{13}}{7}.]$

Note that because? $11$ ?and? $7$ ?are prime, the minimum value of? $x$ ?must involve factors of? $7$ ?and? $11$ ?only. Thus, we try to look for the lowest power? $p$ of? $11$ ?such that? $13p + 1 equiv 0 pmod{5}$ , so that we can take? $11^{13p + 1}$ ?to the fifth root. Similarly, we want to look for the lowest power? $n$ ?of? $7$ ?such that? $13n - 1 equiv 0 pmod{5}$ . Again, this allows us to take the fifth root of? $7^{13n - 1}$ . Obviously, we want to add? $1$ ?to? $13p$ ?and subtract? $1$ ?from? $13n$ because? $11^{13p}$ ?and? $7^{13n}$ ?are multiplied by? $11$ ?and divided by? $7$ , respectively. With these conditions satisfied, we can simply multiply? $11^{p}$ ?and? $7^{n}$ and substitute this quantity into? $y$ ?to attain our answer.

We can simply look for suitable values for? $p$ ?and? $n$ . We find that the lowest? $p$ , in this case, would be? $3$ ?because? $13(3) + 1 equiv 0 pmod{5}$ . Moreover, the lowest? $q$ ?should be? $2$ ?because? $13(2) - 1 equiv 0 pmod{5}$ . Hence, we can substitute the quantity? $11^{3} cdot 7^{2}$ ?into? $y$ . Doing so gets us:

$[(a^{5c}b^{5d}) = frac{11(11^{3} cdot 7^{2})^{13}}{7} = 11^{40} cdot 7^{25}.]$

Taking the fifth root of both sides, we are left with? $a^cb^d = 11^{8} cdot 7^{5}$ .? $a + b + c + d = 11 + 7 + 8 + 5 = boxed{textbf{(B)} 31}$

Solution 2

A simpler way to tackle this problem without all that modding is to keep the equation?as:

$[7*a^{5b}c^{5d} = 11y^{13}]$

As?stated above,? $a$ ?and? $c$ ?must be the factors 7 and 11 in order to keep? $x$ ?at a minimum. Moving all the non-y terms to the left hand side of the equation, we end up with:

$[7^{5b+1}11^{5d-1}=y^{13}]$

The above equation means that? $y$ ?must also contain only the factors 7 and 11 (again, in order to keep? $x$ ?at a minimum), so we end up with:

$[7^{5b+1}11^{5d-1}=7^{13h}11^{13j}]$

( $h$ ?and? $j$ ?are arbitrary variables placed in order to show that? $y$ ?could have more than just one 7 or one 11?as?factors)

Since 7 and 11 are prime, we know that? $5b+1=13h$ ?and? $5d-1=13j$ . The smallest positive combinations that would work are? $b=5,h=2$ ?and? $d=8,j=3$ . Therefore,? $a+b+c+d=7+5+11+8=31$ .? $boxed{textbf{(B)} 31}$ ?is correct.
Solution 1

There are? $4$ ?choices for the first element of? $S$ , and for each of these choices there are? $4!$ ?ways to arrange the remaining elements. If the second element must be? $2$ , then there are only? $3$ ?choices for the first element and? $3!$ ?ways to arrange the remaining elements. Hence the answer is? $frac{3 cdot 3!}{4 cdot 4!} = frac {18}{96} = frac{3}{16}$ , and? $a+b=19 Rightarrow mathrm{(E)}$ .

Solution 2

There is a? $frac {1}{4}$ ?chance that the number? $1$ ?is the second term. Let? $x$ ?be the chance that? $2$ ?will be the second term. Since? $3, 4,$ ?and? $5$ ?are in similar situations?as? $2$ , this becomes? $frac {1}{4} + 4x = 1$

Solving for? $x$ , we find it equals? $frac {3}{16}$ , therefore? $3 + 16 = 19 Rightarrow mathrm{(E)}$
Solution 1

Since $begin{align*} -f(-1) = a - b + c - d = 0 = f(1) = a + b + c + d end{align*}$

It follows that? $b + d = 0$ . Also,? $d = f(0) = 2$ , so? $b = -2 Rightarrow mathrm{(B)}$ .

Solution 2

Two of the roots of? $f(x) = 0$ ?are? $pm 1$ , and we let the third one be? $n$ . Then $[a(x-1)(x+1)(x-n) = ax^3-anx^2-ax+an = ax^3 + bx^2 + cx + d = 0]$ Notice that? $f(0) = d = an = 2$ , so? $b = -an = -2 Rightarrow mathrm{(B)}$ .

Solution 3

Notice that if? $g(x) = 2 - 2x^2$ , then? $f - g$ ?vanishes at? $x = -1, 0, 1$ ?and so $[f(x) - g(x) = ax(x-1)(x+1) = ax^3 - ax]$ implies by? $x^2$ ?coefficient,? $b + 2 = 0, b = -2 Rightarrow mathrm{(B)}$ .

Solution 4

The roots of this equation are? $-1, 1, text{ and } x$ , letting? $x$ ?be the root not shown in the graph. By Vieta, we know that? $-1+1+x=x=-frac{b}{a}$ ?and? $-1cdot 1cdot x=-x=-fraccqle8lm{a}$ . Therefore,? $x=fraccqle8lm{a}$ . Setting the two equations for? $x$ ?equal to each other,? $fraccqle8lm{a}=-frac{b}{a}$ . We know that the y-intercept of the polynomial is? $d$ , so? $d=2$ . Plugging in for? $d$ ,? $frac{2}{a}=-frac{b}{a}$ .

Therefore,? $b=-2 Rightarrow boxed{B}$
By the?Law of Cosines, $begin{align*} AB^2 + BC^2 - 2 AB cdot BC cos alpha = 89 - 80 cos alpha = AC^2 &< 49\ cos alpha &> frac 12\ end{align*}$ It follows that? $0 < alpha < frac {pi}3$ , and the probability is? $frac{pi/3}{pi} = frac 13 Rightarrow mathrm{(D)}$ .
Solution 1

Let? $overline{AC}$ ?and? $overline{BD}$ ?intersect at? $O$ . Since? $ABCD$ ?is a rhombus, then? $overline{AC}$ ?and? $overline{BD}$ ?are?perpendicular?bisectors. Thus? $angle POQ = 90^{circ}$ , so? $OPNQ$ is a?rectangle. Since the diagonals of a rectangle are of equal length,? $PQ = ON$ , so we want to minimize? $ON$ . It follows that we want? $ON perp AB$ .

Finding the area in two different ways, $[frac{1}{2} AO cdot BO = 60 = frac{1}{2} ON cdot AB = frac{sqrt{8^2 + 15^2}}{2} cdot ON Longrightarrow ON = frac{120}{17} approx 7.06 Rightarrow mathrm{(C)}]$

Solution 2 (semi-bash)

Let the intersection of? $overline{AC}$ ?and? $overline{BD}$ ?be? $E$ . Since? $ABCD$ ?is a rhombus, we have? $overline{AC} perp overline{BD}$ ?and? $AE = CE = dfrac{AC}{2} = 8$ . Since? $overline{NQ} perp overline{BD}$ , we have? $overline{NQ} parallel overline{AC}$ , so? $triangle{BNQ} sim triangle{BAE} sim triangle{NAP}$ . Therefore, $[dfrac{NP}{AP} = dfrac{NP}{8 - NQ} = dfrac{BE}{AE} = dfrac{15}{8} Rightarrow NP = 15 - dfrac{15}{8} NQ.]$ By Pythagorean Theorem, $[PQ^2 = NQ^2 + NP^2 = NQ^2 + left(15 - dfrac{15}{8} NQ right)^2 = dfrac{289}{64} NQ^2 - dfrac{225}{4} NQ + 225.]$ The minimum value of? $PQ^2$ ?would give the minimum value of? $PQ$ , so we take the derivative (or use vertex form) to find that the minimum occurs when? $NQ = dfrac{225 cdot 8}{289}$ ?which gives? $PQ^2 = dfrac{225 cdot 64}{289}$ . Hence, the minimum value of? $PQ$ ?is? $sqrt{dfrac{225 cdot 64}{289}} = dfrac{120}{17}$ , which is closest to? $7 Rightarrow boxed{textbf{C}}$ .
The function? $f(x) = sin x$ ?has roots in the form of? $pi n$ ?for all integers? $n$ . Therefore, we want? $frac{1}{x} = pi n$ ?on? $frac{1}{10000} le x le frac{1}{1000}$ , so? $1000 le frac 1x = pi n le 10000$ . There are? $frac{10000-1000}{pi} approx boxed{2900} Rightarrow mathrm{(A)}$ ?solutions for? $n$ ?on this interval.
Solution 1

Consider the graph of? $f(x)=|x-a|+|x-b|+|x-c|$ .

When? $x<a$ , the slope is? $-3$ .

When? $a<x<b$ , the slope is? $-1$ .

When? $b<x<c$ , the slope is? $1$ .

When? $c<x$ , the slope is? $3$ .

Setting? $x=b$ ?gives? $y=|b-a|+|b-b|+|b-c|=c-a$ , so? $(b,c-a)$ ?is a point on? $f(x)$ . In fact, it is the minimum of? $f(x)$ ?considering the slope of lines to the left and right of? $(b,c-a)$ . Thus, graphing this will produce a figure that looks like a cup: $[asy] import graph; size(100); draw((0,6)--(3,0)); xaxis(0,8.5); yaxis(0,10); real f(real x) { return -3(x-2)+5; } real f2(real x) { return -1(x-2)+5; } real f3(real x) { return 1(x-4)+3; } real f4(real x) { return 3(x-7)+6; } draw(graph(f,0,2)); draw(graph(f2,2,4)); draw(graph(f3,4,7)); draw(graph(f4,7,8.5)); draw((2,-0.25)--(2,0.25)); label("a",(2,0),N); draw((4,-0.25)--(4,0.25)); label("b",(4,0),N); draw((7,-0.25)--(7,0.25)); label("c",(7,0),N); dot((2,5)); label("P",(1.9,5.2),E); [/asy]$ From the graph, it is clear that? $f(x)$ ?and? $2x+y=2003$ ?have one intersection point if and only if they intersect at? $x=a$ . Since the line where? $a<x<b$ ?has slope? $-1$ , the positive difference in? $y$ -coordinates from? $x=a$ ?to? $x=b$ ?must be? $b-a$ . Together with the fact that? $(b,c-a)$ ?is on? $f(x)$ , we see that? $P=(a,c-a+b-a)$ . Since this point is on? $x=a$ , the only intersection point with? $2x+y=2003$ , we have? $2 cdot a+(b+c-2a)=2003 implies b+c=2003$ .?As? $c>b$ , the smallest possible value of? $c$ ?occurs when? $b=1001$ ?and? $c=1002$ . This is indeed a solution?as? $a=1000$ ?puts? $P$ ?on? $y=2003-2x$ , and thus the answer is? $boxed{mathrm{(C)} 1002}$ .

This indeed works for the two right segments of slope? $1$ ?and? $3$ . We already know that the minimum is achieved between slopes? $-3$ ?and? $-1$ ?with? $b+c=2003$ : $[2003-2x=-a-b+c+xlongrightarrow 3xne a+b-c+2003 {b<x<c}rightarrow (3b,3c)ne a+2brightarrow b>atext{ (true)}]$ $[2003-2x=-a-b-c+3xlongrightarrow 5xne a+b+c+2003 {x>c}rightarrow (5c,+5infty)ne a+2b+2crightarrow 3c>a+2btext{ (true)}]$ Indeed, within the restricted domain of? $x$ ?in each segment, these inequalities prove to be unequal everywhere. So? $y=2003-2x$ ?is strictly below? $y=|x-a|+|x-b|+|x-c|$ ?at these domains.

Solution 2

Step 1: Finding some promising bound

Does the system have a solution where? $xleq a$ ?

For such a solution we would have? $y=(a-x)+(b-x)+(c-x)$ , hence? $2x+(a+b+c-3x)=2003$ , which solves to? $x=a+b+c-2003$ . If we want to avoid this solution, we need to have? $a+b+c-2003>a$ , hence? $b+c>2003$ , hence? $cgeq 1003$ . In other words, if? $c<1003$ , there will always be one solution? $(x,y)$ ?such that? $xleq a$ .

Step 2: Showing one solution

We will now find out whether there is a? $c<1003$ ?for which (and some? $a,b$ ) the system has only one solution. We already know of one such solution, so we need to make sure that no other solution appears.

Obviously, there are three more theoretically possible solutions: one? $x$ ?in? $left(a,bright]$ , one in? $left(b,cright]$ , and one in? $left(c,inftyright)$ . The first case solves to? $x=2003+a-b-c$ , the second to? $3x=2003+a+b-c$ , and the third to? $5x=2003+a+b+c$ . We need to make sure that the following three conditions hold:
1. $2003+a-b-cnotinleft(a,bright]$
2. $frac{2003+a+b-c}3notin left(b,cright]$
3. $frac{2003+a+b+c}5notinleft(c,inftyright)$ .
Let? $c=1002$ ?and? $b=1001$ . We then have:
1. $2003+a-b-c=a$
2. $frac{2003+a+b-c}3 = frac{2002+a}3 leq frac{2002+1000}3 < 1001 = b$
3. $frac{2003+a+b+c}5 = frac{4006+a}5 leq frac{4006+1006}5 < 1002 = a$
Hence for? $c=1002$ ,? $b=1001$ ?and any valid? $a$ ?the system has exactly one solution? $(x,y)=(a,2003-2a)$ .

Step 3: Proving the optimality of our solution

We will now show that for? $c<1002$ ?the system always has a solution such that? $x>a$ . This will mean that the system has at least two solutions, and thus the solution with? $c=1002$ ?is optimal.
1. As?we are looking for a? $c<1002$ , we have? $b+cleq 2001$ , hence? $2003+a-b-c > a$ . To make sure that the value falls outside? $left(a,bright]$ , we need to make it larger than? $b$ , thus? $2003+a-b-c > b$ , or equivalently? $2003+a > 2b+c$ .
2. The condition we just derived,? $2003+a > 2b+c$ , can be rewritten?as? $2003+a+b > 3b+c$ , then?as? $2003+a+b-c > 3b$ , which becomes? $frac{2003+a+b-c}3 > b$ . Thus to make sure that the second value falls outside? $left(b,cright]$ , we need to make it larger than? $c$ . The inequality? $frac{2003+a+b-c}3 > c$ ?simplifies to? $2003+a+b > 4c$ .
3. To avoid the last solution, we must have? $frac{2003+a+b+c}5leq c$ , which simplifies to? $2003+a+b leq 4c$ .
The last two inequalities contradict each other, thus there are no? $a,b,c$ ?that would satisfy both of them.

Conclusion

We just showed that whenever? $c<1002$ , the system has at least two different solutions: one with? $xleq a$ ?and one with? $x>a$ .

We also showed that for? $c=1002$ ?there are some? $a,b$ ?for which the system has exactly one solution.

Hence the optimal value of? $c$ ?is? $boxed{mathrm{(C)} 1002}$ .
The first point anywhere on the circle, because it doesn't matter where it is chosen.The next point must lie within? $60$ ?degrees of arc on either side, a total of? $120$ ?degrees possible, giving a total? $frac{1}{3}$ ?chance. The last point must lie within? $60$ ?degrees of both.The minimum area of freedom we have to place the third point is a? $60$ ?degrees arc(if the first two are? $60$ ?degrees apart), with a? $frac{1}{6}$ ?probability. The maximum amount of freedom we have to place the third point is a? $120$ ?degree arc(if the first two are the same point), with a? $frac{1}{3}$ ?probability.As?the second point moves farther away from the first point, up to a maximum of? $60$ ?degrees, the probability changes linearly (every degree it moves, adds one degree to where the third could be).Therefore, we can average probabilities at each end to find? $frac{1}{4}$ ?to find the average probability we can place the third point based on a varying second point.Therefore the total probability is? $1timesfrac{1}{3}timesfrac{1}{4}=frac{1}{12}$ ?or? $boxed{text{(D)}}$