與洲際彈道導彈有關的簡單數學

所謂“洲際彈道導彈”（intercontinental ballistic missile，ICBM），通常是指射程大于8000 km的遠程彈道式導彈。它是一個國家戰略核力量的重要組成部分，主要用于攻擊敵國領土上的重要軍事、政治和經濟目標。在上世紀60-70年代的冷戰高峰時期，美國和蘇聯在本國的不同地點部署了數千枚搭載核彈頭的洲際彈道導彈，目標是對方的主要城市和導彈發射井。這是一場非常危險的“零和博弈游戲”，后來有人用一個非常形象的詞——“確保相互摧毀”來形容這種狀態，而“確保相互摧毀”的英文首字母縮寫為MAD，恰好與英文單詞“瘋狂的”相同。

這種僵局一直持續到上世紀80年代后期，特別是在美國新提出要搞“星球大戰”計劃之后。今天，洲際彈道導彈技術出現了向全球擴散的趨勢，很多國家都紛紛研制成功或準備研制自己的洲際導彈或遠程導彈，如朝鮮、伊朗等。要知道，洲際彈道導彈這種國之重器的研制、測試和部署費用絕對稱得上是一個天文數字，以美國為例，其1枚洲際彈道導彈的全壽命使用周期費用大概為10億美元，而2016年世界上最貧窮的國家津巴布韋總人口為1615萬，人均GDP為0.1美元，即其國民生產總值為0.016億美元，所以換算下來，美國1枚洲際彈道導彈的費用相當于津巴布韋625年的國民生產總值！除了價格不菲，洲際彈道導彈的技術也極為復雜，幾乎涉及現代工業領域的各個方面。

在此，我們掛一漏萬，只對洲際導彈從發射點運動到最終命中點的運動學和動力學特征進行一番極其簡單的探討，用“簡單”的數學來計算一下諸如導彈飛抵離地球表面最高點時的高度H、耗費時間τ、在地球表面上的投影距離（即射程）L及其影響因素，以此對洲際導彈這種迄今為止人類歷史上最具威懾力的武器來一個數理方面的“管中窺豹”。我們以下面這幅示意圖為討論的起點，該圖顯示的是典型的洲際彈道導彈的飛行軌跡：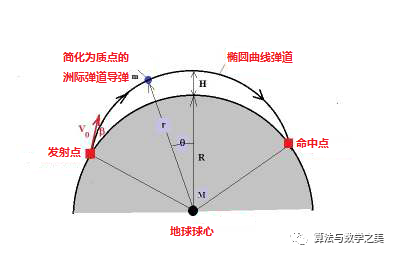

上圖：洲際導彈飛行彈道的簡要示意圖。從上圖中我們知道，洲際彈道導彈走的是一條從發射點開始，一直延續到命中點的橢圓曲線彈道，這條運動軌跡基本上位于由發射點、命中點和地球球心確定的平面內。忽略所有的空氣阻力，我們通過能量守恒定律和角動量守恒定律可以得到下面兩個等式 ：

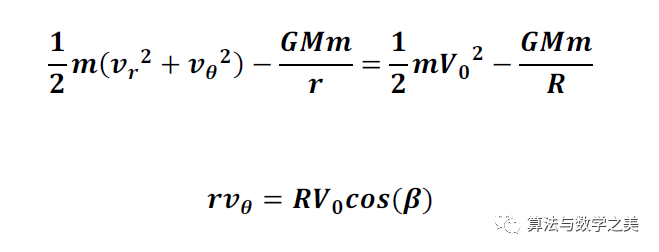
式中，vr和vθ分別是洲際導彈徑向和切向的速度分量，m是導彈的質量，M和R是地球的質量和半徑，V0和β是導彈發射時的速度和發射時與水平線所成的角度，G是萬有引力常數。通過聯立這兩個方程，并設GM=gR2，其中g是地球表面的標準重力加速度，我們可以得到下面的等式：

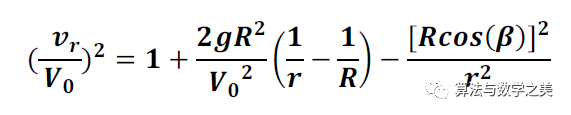
要想求出導彈到達地球表面上方最高點的高度H，我們只需令vr為零，這樣便得到了下面的二次方程：

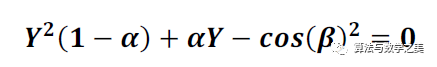
式中，Y=r/R，α=2gR/V02。一般情況下，Y和α的值都大于1。當β=π/2時，對應的是一種特殊情況，即導彈垂直發射。當α=1時，可以求出此時的速度V0=√(2gR)。對于地球來說，這個數值等于11.2 km/s，也就是第二宇宙速度。在這種情況下，Y的值為無窮大。對于(cosβ)的值，當其不等于零時，上面的二次方程有一個正解：

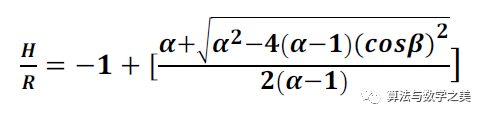
我們可以計算一下以π/3、π/4和π/6的角度發射洲際彈道導彈的結果，然后以α為橫軸，H/R為縱軸，繪制出二者的關系圖，如下圖所示：

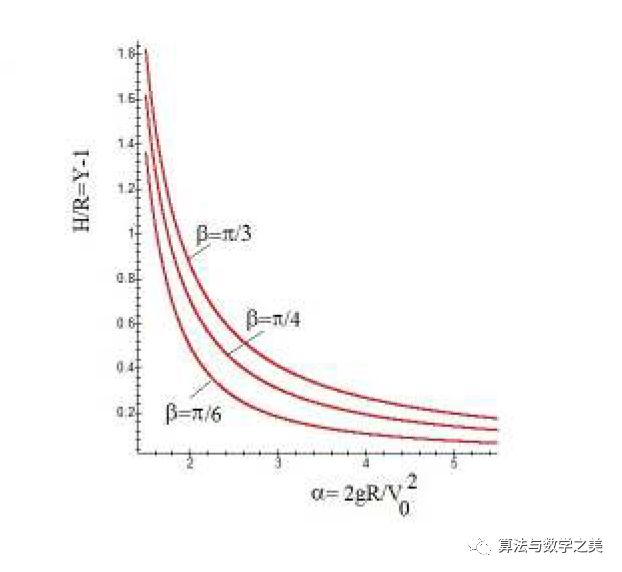
上圖：洲際導彈不同的發射角度對射高的影響。從圖中我們可以看出，發射速度越大，導彈上升的高度就越高。當α=1時，上升的高度將變為無窮大；而當V0趨向于零時，導彈上升的高度為零。如果我們設cos(β)=0，并假設H/R<<1，使α>> 1，便可得到H=V02/2g這一經典結果。我們可以使用前面計算的徑向速度分量來求解導彈飛抵最大高度時所需的時間，并將該結果乘以2（因為上升段和下降段是對稱的），以得到命中目標的時間τ，計算公式如下：

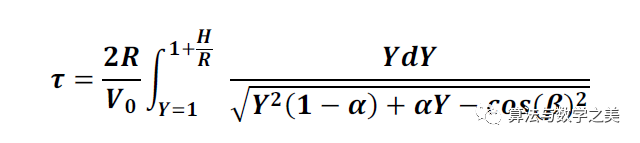
現在，讓我們來實際計算一下這個積分：我們不妨選擇實際值cos(β)=√3/2，α=4，H/R=√7/6-1/3=0.1076。導彈發射速度和角度分別為V0=5.593 km/s和β=π/6。取地球半徑R=6378 km，計算得到τ=991 s=16.5 min，再考慮到空氣阻力造成的速度下降，因此總時間差不多在20 min左右，這個數字與實際情況是相符的：根據美國方面披露的資料，其如果遭到俄羅斯的洲際核導彈打擊的話，預警時間基本就在20 min左右。還有一個問題就是，在這種情況下，發射點和命中點之間的地球表面投影距離，即導彈的射程L是多少。我們通過角動量守恒定律可知vθ=RV0cos(β)/r，而由于H/R<<1，因此r可以很好地用R來近似。這樣，我們就求出了地球表面上的投影距離L約為：

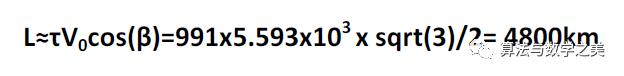
在上面的例子中，求出的數字比莫斯科和紐約之間的距離（7525 km）要短不少。要想增加地球表面的投影距離L，也就是提高導彈的射程，只需要簡單地增加V0和β即可。通過使β=√(gR)=7.9 km/s，并且讓β趨近于零，可以將導彈打出一條近似的繞地圓形軌道。說到這里，可能很多讀者已經明白了：7.9 km/s正好是第一宇宙速度，發射低軌道衛星就是以這一速度入軌的。最后要強調的一點是，地球是時刻在旋轉的，因此洲際彈道導彈實際上是在“追逐”一個不斷移動的目標。不過，解決這一問題是件很容易的事，只需要對命中點的經度進行修正就可以了，準確一點說是按照(τ/1440 min)2πRcos(目標緯度值)的標準進行修正，其可以直接寫入導彈彈載計算機的飛行控制程序代碼中。

根據美國方面披露的相關資料，冷戰期間，如果對蘇聯首都莫斯科（北緯55.75°，東經37.62°）發起攻擊，在不修正經度的情況下，導彈在經過τ=20 min的飛行后，將落在莫斯科以東約313 km處。另外，地球的自轉也可以解釋這樣一個事實：在極地軌道上運行的間諜偵察衛星可以觀測到其軌跡下方地球表面的每個點，而不需要進行任何軌道修正。

在洲際彈道導彈的實際發射中，幾乎總是以垂直于地面的姿態進行發射的，在起飛后幾分鐘內便迅速達到預期的速度V0和發射角β。導彈在大部分運動時間內都是憑借慣性自由飛行的，這就使預測導彈的運動軌跡并予以攔截成為了可能。在1991年爆發的海灣戰爭中，伊拉克曾使用飛行速度相對較慢（5倍聲速，約相當于1700 m/s）的“飛毛腿”彈道導彈攻擊以色列，其相當一部分被美國雷錫恩公司研制的“愛國者”防空導彈武器系統攔截。這已經是個不小的進步了，要知道，在彈道導彈誕生后，很長一段時間內人們對其基本上是束手無策。

例如，二戰期間，即導彈投入實戰后不久，英國人雖成功地使用高速戰斗機和摧毀發射場的方式對德國人的V1巡航導彈進行了有效的防御，但卻完全無法對抗以數倍聲速飛行的V2彈道導彈。即使在今天，要想攔截以20倍甚至30倍聲速飛行的洲際彈道導彈也不是一件容易的事。

最后，看了這么多“枯燥無味”的數學和力學公式之后，我們來輕松一下。關于洲際彈道導彈，有這樣一則有趣的“軼事”：二戰期間，美國總統羅斯福的科學顧問范內瓦·布什（Vannevar Bush）在1945年曾說過這樣一句“名言”：“真正堪用的洲際彈道導彈永遠不可能成為現實。”其實這種名人因為一時的“短視”而發表荒謬言論的例子比比皆是，如發現了原子核的盧瑟福勛爵在1933年就曾發布過這樣一則糟糕的聲明：“任何聲稱原子核能成為一種能量來源的人都是在胡說八道。”