怎樣學習數學效率會更高？

小學、中學甚至到大學，都得學數學。為什么要學這么多數學呢? 伽利略說：“大自然，這部偉大的書，是用數學語言寫成的。”前美國總統科學顧問艾德華·大衛說：“很少人認識到當今如此被廣泛稱頌的高技術在本質上是一種數學技術。”數學是科學之母，是物理學、力學、天文學、化學、生物學的基礎，為其提供了描述規律的語言和探索未知世界的工具。

數學如此重要，怎樣才能更高效地學習數學？像數學家那樣學習數學才是更高效的學習思維和方法。

一、數學家究竟是如何思考的？

菲爾茲獎得主Atiyah：“我們欣賞數學之美動用到的大腦部分與欣賞音樂、藝術和詩歌時動用的大腦部分完全一樣。這是個大發現”。數學家的思考方法到底是怎樣的？他們質疑一切；反過來又如何；利用逆否；考慮極端情形；構造自己的例子；假設用在哪里；從復雜的一邊開始；如果有……，那么會怎樣；交流等。

在學校教育中，老師是如何引導孩子學習數學呢？老師受教育進度和教學計劃約束，往往忽略數學中最美的知識。數學中最美的往往是最基本的，最基本的往往不會在考試中出現。為了實施教學計劃，老師們往往會對這些最美的知識一筆帶過，很少能認真領著孩子欣賞這些美的知識。天真爛漫的孩子能夠在私下的生活中能慢慢琢磨和感受這些美的數學知識的人，是少之又少的。名校往往把這些任務壓給孩子們，悟性高的往往勉強應付，悟性低的遺害終生。另外，如今的孩子們，都是忙碌的孩子，家長早已把孩子們的時間安排的滿滿的，哪有時間琢磨、欣賞和感受這些美的數學知識。

培訓機構模式：例題講解—習題套。這種模式在降低數學題目難度的同時，剝奪了孩子自己思考和探索的機會。聰明孩子在此教育模式之下，很快能獲得理想成績；普通孩子將會消耗掉自己的興趣和動力。一旦孩子沒有興趣和動力是非常危險的事情，像現實生活中，有些孩子雖然獲得奧數獎牌并成功保送到理想大學，但最終甚至沒能順利拿到學位進而被勸退。

堅持學數學的孩子，靠其內心的標準，也靠他們在數學直覺上的微小收獲所帶來的巨大喜悅。

培育和激發孩子的探索精神，是教育中的重要任務。探索精神是數學家以及其他科學家所具備的重要精神。美國和俄羅斯在探索性教學方面積累了豐富的成功經驗，培育了大量的著名數學家和科學家。探索性教學有兩種道路：一是之字形，爬起來不累，適合游客和大部隊；二是攀巖，爬行者會覺得累而快。下面舉靖學習數學過程中的一個例子：

如圖，O為三角形ABC中的一個點。O到三角形三邊的垂線分別交三條邊于D、E、F。設線段OA、OB、OC的長度分別是x、y、z，線段OD、OE、OF的長度分別是p、q、r，那么埃爾德什-莫德爾不等式為：

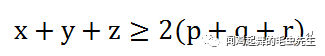
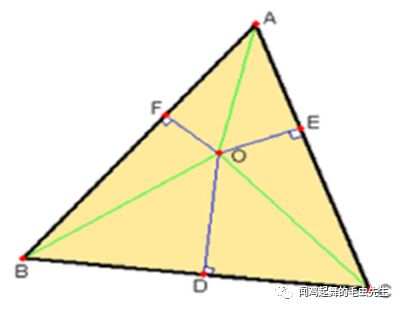
這個題目是高中學術活動數學課本《數學（高中上冊）》（華東師范大學第二附屬中學（實驗班用））第五章的內容。靖第一次拿起這本書時，前面的內容都沒學習過，隨意翻到這一頁，就被這道題目給迷住了。

第一次看這道題目時，靖很平靜地告訴我，他看不懂解題過程。我說：“看不懂就看不懂，沒關系，前面鋪墊的很多知識你都沒學，怎么可能能看懂呢？很多符號你都不認識。”

過了幾天，靖第二次禁不住又找到這本書，又翻到這道題目，又看了一遍，很平靜地告訴我，他沒看懂解題過程。我答：“看不懂，沒關系，以后再想辦法。”放下書出去玩玩吧！我以為靖早已忘了這道題目。

又過了幾天，靖第三次翻到這個題目，他看懂了，而且很激動很熱情地告訴我：“這道題目我看懂了。”我一臉笑容地說：“給我講講。”結果，靖就給我先做了知識鋪墊，把所有可能用到的定理和知識先給我講了一遍，然后才講這道題目的證明過程。

又過了幾天，靖第四次告訴我：“他已經會用至少五種方法證明這道題目。”

靖這個題目的學習過程，就是典型的探索性學習過程。他走的路徑是攀巖式路徑。

像數學家那樣學習數學：學習教材時，自己先思考例題，如果不會再看例題講解；如果題目的結論變成條件，條件變成結論，會怎樣；改編題目，自己出題，也是一種很好的思路。這種學習數學的思路會讓孩子有更強大的動力和興趣去探索，持續維護孩子的興趣，提升學習效率。

以靖為例，靖在幼升小那個暑假，花了大約10天的時間，完全像個小數學家那樣，無論是出去玩還是洗腳或洗臉，一直在思考數學問題。在這個過程中，他是不是平跑過來向我確認他思考的結果的正確性，然后滿意地離開。

例1：2+2+2+2+2+2=？這也是6個2相乘呀！說明12里有6個2。在此，我明白了整數的加減乘除運算規則。

例2：4x25=100，8x12.5=100，16x6.25=100，這三個算式就是一個乘數除以2，一個乘數乘以2，結果應該不變。在此，我明白了小數如何進行乘除運算。

 

二、如何刷題效率會更高

刷題的目的是用最短的時間讀懂題目和問題，并理清思路，短時間接觸大量題型的各種方法。具體方法：將答案放在一邊，讀題圈數字單位和要點，在第一直覺中給出解題思路。然后對照答案，如果完全一樣，直接跳過。如果不一樣，對比答案，尋找差異，思考答案的方法好在哪里。最后合上答案在腦子里解一遍題。

第一種刷題：計時練習，常年堅持。把積攢下來的經典題目湊成一張卷子做，這種方法的要義在于常年堅持，不在于某次刷題的多少。

第二種刷題：刷錯題本，重視數學難題的消化。針對那些不會做的題，看了答案，沒有很好掌握的題。這種題目，需要刷好幾遍，才能真正搞會。此種方法的要義在于：堅持，堅持，再堅持。

第三種刷題：小組訓練法，提升悟性。兩三個人一伙，互相給對方當教練，將大家不會的題，分為三組，每組題由一個人負責看答案，來當其他兩人的教練，允許提問，教練給予提示，靠這個過程把題做出來。

刷題的導出效果：學生可以將難題放在腦子里翻來覆去地想，突然有了靈感，也算是內在的隨機性的自我獎勵。難題相對個人能力不同而不同。通過第一遍刷題，找出難題，再集中精力二刷或三刷難題，悟性和能力必將會有大幅度提升。

 

三、怎樣刷題才能刷出“數覺”？

日本菲爾茲獎得主小平邦彥，創造了數覺（NumberSense）這個名詞。他提出：了解數學是看出數學的現象來，這種“看”是憑某種感覺來意會的，有數覺的人念起數學來就得心應手得多。“數覺”已被寫入西方國家的中小學數學教材中，開始被心理學家研究。

數覺不能簡單地理解為對數學的感覺，是人們在實踐經驗和已有知識的基礎上，形成和發展起來的一種認識能力，是持久探索和思考的結果，而不是憑空想象的結果。數覺是人腦對數學對象、結構及其關系的某種直接領悟或洞察。數覺具有突發性、直接性、創造性和或然性特征。

突發性：數覺往往受視覺觸發，突然地領悟道理，做出判斷，得出結論。直接性：在直覺思維中，數學是一種邏輯的跳躍，通常不作詳盡的分析和推理，直接接觸結果，因而具有直接性。創造性：數覺思維的結果通常會表現出新的突破，得到新的結論，因此帶有極強的創造性。或然性：數覺是一種邏輯的跳躍，沒有經過嚴格的邏輯思考與推理，因此其所得的結論未必正確，具有或然性。

數覺涉及更多非理性因素，即理性之外的認識、意識、心理因素。數覺的培養應重在基于孩子已有的知識經驗和生活經驗，鼓勵孩子經常做實驗性數學作業，給孩子創造探索與思考的機會，加強孩子合情推理等能力的培養。

1. 在平時生活中，創設生活數學情境，激發孩子研究數學的興趣，誘發孩子的直覺思維，促進自覺探究。例如，靖大概5歲時，爸爸隨便編了一個題目。

我們一家去飯店吃餃子，要了兩盤總計48個，花費同樣的時間，爸爸吃3個餃子，媽媽吃2個餃子，靖靖吃1個餃子，問最后，爸爸、媽媽和靖靖分別吃了多少個餃子？

靖靖很快答說：靖靖吃了8個，媽媽吃了16個，爸爸吃了24個餃子。

2. 在平時生活中，適當加大數學知識難度和滲透科學認識的引導，重視孩子對科學方法、科學價值的掌握和理解，加強孩子整理知識和重組知識能力。

例如，如圖，半徑為5厘米的圓內和圓外各有一個正方形，圓內正方形的四個頂點都在圓周上，圓外正方形的四條邊和圓都只有一個接觸點。問大正方形的面積比小正方形的面積大多少？

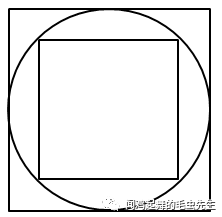
孩子如果受到知識的限制，無法用分別求出大小正方形的邊長，在求出面積，最后求出它們的差這種思路。由于圓、正方形都是中心對稱圖形，圓內接小正方形可以旋轉，旋轉到特殊位置就能發現圖形間的大小關系（如圖）。顯然，小正方形的面積是大正方形面積的一半。

 

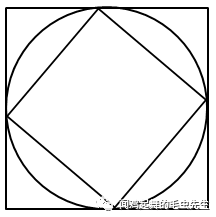
這種引導，有利于孩子探索、發現和解決數學問題，順利抓住數學知識的本質，提升孩子的數覺水平。

3. 基于孩子已有的知識和經驗，重視數學學習材料的選取，營造真是的數學活動教學情境，鼓勵孩子做實驗性探索。例如，引導孩子學習“統計與概率”知識時，嘗試從生活中收集數據，進行整理、統計和分析，從中尋找數學知識與規律。

下表是一次我和孩子玩脈搏測量的實驗結果。經過與孩子共同討論、交流之后發現，測量一個人的脈搏用20~30秒比較適宜。通過做實驗，可以激發孩子的數學學習興趣和好奇心，提升孩子“數覺”能力。

4. 引導合情推理，訓練創造性思維。合情推理的基本格式是，首先給出一個猜想，然后通過多種方式找出理由去證實，以增強或否定其猜想的合理性。

給孩子一組不同類型、不同大小的平行四邊形，與孩子一起探討平行四邊形的相關性質。用量角器測量四個角，通過對折比較對角大小和對邊的大小，通過平移觀察對邊的平行性質等。這種實踐性測量和觀察，提升了孩子的感知認識。