【A-Level物理題目解析】數格子的藝術

數格子的藝術

題目：

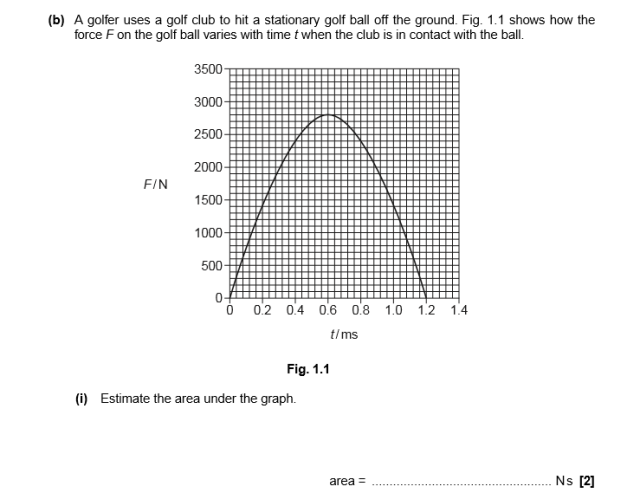
解圖像題的第一步是先審清題目，看一下這個graphs的橫豎坐標分別為什么物理量，它們的單位是什么？以本題為例，X軸是time，單位是ms。Y軸是force，單位是N。所以我們就清楚的了解到，這題是一道force-time graph。下一步，是要看清圖像的形狀。一般來說，我們的圖像分為linear graph 和?nonlinear graph。他們分別表示Y軸這個物理量與X軸的物理量是否是正比的關系。在物理學中，對于linear?graph， 我們應該特別注意gradient是哪個物理量。對于nonlinear graph 我們應該特別注意曲線下的area是哪個物理量。舉例來說，對于constant?force，直線下方與坐標軸的面積就是一個矩形，矩形的長乘以寬就是這段線段的投影面積。通過公式我們知道，Fxt應該是物理量impulse。

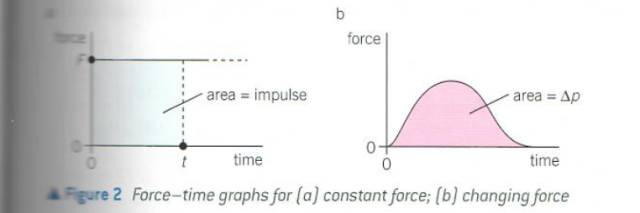
同理可證，對于changing?force，我們也不難想出來：曲線下的面積也是impulse。回到這道例題，為了求面積，現在需要數一下曲線以下到坐標軸以上的小格子的數量。?這個可能是有些同學最頭疼的事情，這么小的格子密密麻麻，我們需要“放大鏡”。就是這段所包含的面積。

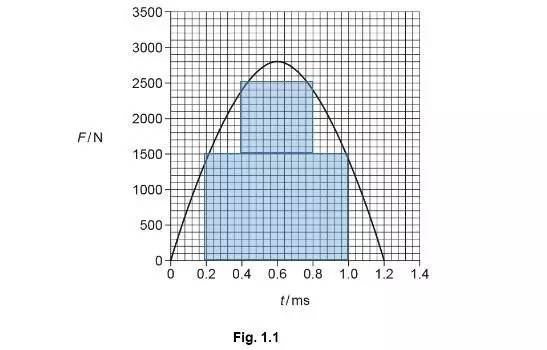
同學們也可以在屏幕上數一下，超過半格的算一個，不超過半格的不用算。有沒有同學數出來一共多少個格子啊？對的，答案是550個。但是有的同學說，數格子太麻煩。有的同學說，我都快有密集恐懼癥。那可怎么辦。不用慌，今天主頁君給大家講一下數格子的藝術。我們通過三個圖，解釋一下，數格子的三種辦法。

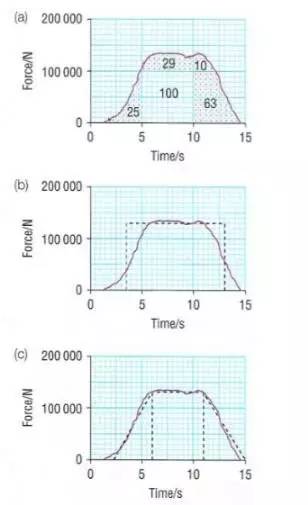
第一，?分割法。把容易標記出來的格子圈成一個一個矩形，這樣，即使剩下的格子一個一個數，也減少了很多的工作量了。

第二，?補充法。其實，既然小格子超過半格的算一個，不超過半格的不用算。那么從宏觀來說，也可以找出一個大的矩形，把邊邊角角的地方補充到曲線下面。這樣總數算出來的矩形面積也是很準確的。

第三，?相似法。把圖像進行無限分割，分割為我們可以計算出來的幾何圖形，然后通過數學面積公式計算。

所以本題答案是：

(i)?2.2 Ns {allow 2.0 to 2.4}

(ii)?Impulse QWC must be spelled correctly

(iii)?recall of Impulse = change in momentum OR I = mv OR mv –mu ?(mv = 2.2 hence v = 2.2/0.046) v = 47.8 ms-1 (hence about 50) (2.0 gives 43.5, 2.1 45.7, 2.3 50, 2.4 52.2)