翰林國際教育,國內國際競賽領域的開拓者與引領者。我們不僅是系統輔導與深度教研的先行者,更為整個行業提供權威的賽事資訊與海量真題講義。在數學、物理、化學、生物、計算機、商科、數模等核心領域,我們的戰績長期穩居頭部領先地位,屢屢斬獲國家隊級別最高榮譽。作為同時擁有學科培訓、AP國際學校及美高資質的權威教育組織,我們為學生提供一站式的卓越培養體系,助力英才邁向世界頂尖學府。
AMC10數學競賽歷年高頻考點深度
一、 代數與函數:占比約35%
1. 方程與不等式
? 一次/二次方程:不僅是簡單求解,更側重含參方程的討論(參數范圍、根的性質判斷)。例如,給定根的關系(如互為倒數、相反數)反推參數值。
? 高次方程:通過因式分解(分組、十字相乘)、代換法(如令 y = x + frac{1}{x} )降次求解。
? 不等式:重點是一元二次不等式、絕對值不等式的求解與幾何意義(數軸上的距離)。常出現求整數解個數或解集范圍的問題。
2. 函數與圖像
? 函數性質:深入理解定義域、值域、單調性、奇偶性,并能從圖像中讀取信息。
? 函數變換:熟練掌握平移(“左加右減,上加下減”)、伸縮、對稱等變換對解析式的影響。常考多種變換復合后的函數求值。
? 特殊函數:重點復習絕對值函數 f(x) = |ax+b| 和取整函數 f(x) = [x] 的圖像、性質與方程求解。這類題綜合性強,易設陷阱。
3. 數列與規律
? 等差數列/等比數列:熟練應用通項公式、求和公式,特別是等比數列求和公式 S_n = a_1 frac{1-r^n}{1-r} 。
? 遞推數列:通過前幾項找出規律,寫出通項或求和。常與數論結合,要求寫出某項的個位數字或余數。
二、 幾何:占比約30%,直觀與推理并重
幾何題注重數形結合,既考查計算也考查邏輯證明,是區分度較高的模塊。
1. 平面幾何
? 三角形:相似三角形的判定與性質是重中之重,常與勾股定理、特殊角三角函數值(30°, 45°, 60°) 結合求邊長。正弦定理、余弦定理也時有考查。
? 圓:必須熟練掌握圓冪定理(相交弦定理、切割線定理)、圓周角與圓心角關系。常見題型是求圓中線段長度或角度。
? 多邊形與面積:常考正多邊形、梯形、菱形等的性質。面積計算技巧包括割補法、等積變換。
2. 解析幾何
? 直線與圓:求直線斜率、方程(點斜式)、兩直線交點。求圓的方程、直線與圓的位置關系(相交、相切、相離)。
? 距離與面積:計算點與點、點與直線的距離。給定坐標求多邊形面積(常用鞋帶公式)。
3. 立體幾何
? 主要考查長方體、正方體、圓柱、圓錐的基本性質,如求體積、表面積、空間兩點最短路徑(展開圖)。
三、 數論:占比約15%,難度的體現
數論是AMC10的特色與難點,旨在選拔數學思維突出的學生,通常出現在中后部題目。
1. 整數的性質
? 整除特征:2, 3, 4, 5, 8, 9, 11等的快速判斷法則必須熟記。常考“用數字組數”問題,如“用1-9各一次組成能被11整除的數”。
? 質數與合數:判斷質數、分解質因數、求約數個數。關鍵定理:唯一分解定理。
? 奇偶性分析:利用奇偶性進行邏輯推理和排除選項,是解決數論和組合題的重要技巧。
2. 模運算與同余
? 這是數論難題的主要來源。理解模運算的基本性質(如 (a+b) mod m , (a times b) mod m )。
? 尋找周期規律:常要求計算 a^n mod m 的余數,通過尋找指數冪的個位數字或余數的循環周期來求解。
? 中國剩余定理:雖不直接考查定理本身,但考查其思想,即解方程組 x equiv a pmod{m}, x equiv b pmod{n} 。
四、 計數與概率:占比約20%
該模塊考查邏輯的嚴謹性和思維的靈活性,是近年命題的熱點。
1. 計數原理
? 排列與組合:這是絕對核心。必須準確區分“有序”(排列A)和“無序”(組合C)。常考分組問題、隔板法、圓排列、捆綁法與插空法。
? 容斥原理:用于解決重疊計數問題,如求兩個或多個集合的并集元素個數。公式: |A cup B| = |A| + |B| - |A cap B| 。
2. 概率
? 古典概型: P = frac{text{滿足條件的情況數}}{text{所有可能的情況數}} 。難點常在于準確計算出分子和分母。
? 幾何概型:利用長度、面積或體積的比例來求概率。讀題時需注意“均勻隨機”等關鍵詞。
? 條件概率與獨立事件:理解概念,并能用乘法公式 P(AB) = P(A) cdot P(B|A) 計算。
五、 備考策略與高頻考點融合
1. 專題突破與交叉融合
? 后期復習需重點關注代數與幾何的結合(如建立坐標系解決幾何問題)、數論與計數的結合(如求滿足數論條件的數字個數)、概率與方程的結合
2. 真題導向與模擬訓練
? 歷年真題是最佳素材。通過精做真題,熟悉上述高頻考點的出現形式、難度和陷阱設置方式。
? 進行限時模考,鍛煉在75分鐘內從前往后、先易后難的答題節奏,并實踐“不會就空”的得分策略。
AMC10考前2個月高效沖刺策略
一、 精準診斷與針對性強化
最后兩個月沖刺的核心在于精準定位薄弱環節并進行高強度專項突破,避免盲目刷題。
1. 知識圖譜漏洞分析
? 通過近3年真題模擬測試,系統分析錯題類型,建立個人知識薄弱點矩陣。重點區分知識性失分(公式不熟、概念混淆)、思維性失分(思路錯誤、無法建模)和心理性失分(粗心、時間分配不當)。
? 使用錯題追蹤系統,對常錯知識點進行標記歸類。例如:若在數論的同余問題連續出錯,則需專項復習模運算性質、費馬小定理應用等核心內容。
? 制定15日強化計劃:前5日主攻代數與函數(含數列),中間5日突破幾何與三角,后5日攻堅數論與組合概率,確保知識模塊全覆蓋。
2. 高頻考點深度聚焦
? 代數:重點強化復雜因式分解技巧(分組、換元)、高次方程韋達定理應用、函數圖像變換與性質綜合題。
? 幾何:專項訓練圓冪定理與相似三角形的綜合證明、立體幾何空間思維題、解析幾何快速計算技巧。
? 數論:熟練掌握整除特征快速判斷法、同余方程解法、中國剩余定理的簡化應用。
? 組合:加強復雜排列組合問題(捆綁法、插空法)、概率與統計結合題、圖論基礎問題的建模求解。
二、 真題實戰與時間策略優化
沖刺階段需通過高強度模擬訓練提升應試能力,重點優化時間管理和答題策略。
1. 全真模擬考試環境
? 每周完成2-3套近年真題,嚴格遵循75分鐘限時,使用答題卡填涂,完全模擬考場環境。
? 時間分段訓練:
▪ 前30分鐘:強制完成1-15題,訓練基礎題速答能力(平均2分鐘/題)
▪ 中間30分鐘:專注16-22題,提升中檔題準確率(平均3-4分鐘/題)
▪ 最后15分鐘:攻堅23-25題+檢查,培養難題抉擇能力
? 建立時間預警機制:每10題設定完成時間節點(如30分鐘時應完成前15題)
2. 智能答題策略應用
? 三遍答題法:
▪ 第一遍:快速解答確信會做的題目(目標20題)
▪ 第二遍:攻克有思路但需計算的題目(目標4題)
▪ 第三遍:專項突破難題或檢查標記題
? 選擇性放棄原則:對超過5分鐘無思路的題目立即標記跳過,確保會做題目的得分率。利用"空題得1.5分"規則,規避盲目猜題風險。
? 答案驗證技巧:培養代入檢驗、極端值驗證、量綱分析等快速驗算習慣,減少粗心失分。
三、 思維深化與創新解法訓練
突破高分需要超越常規思維模式,培養解決新穎問題的能力。
1. 多解法思維拓展
? 對經典難題(如2021B卷25題)進行一題多解訓練,比較代數法、幾何法、數論法的效率差異。
? 開展命題逆向工程:針對典型結論反推條件設置,深度理解出題邏輯。
? 學習構造法證明:掌握反證法、數學歸納法等在組合、數論問題中的應用。
2. 創新題型應對策略
? 分析近3年新題型趨勢:如跨模塊綜合題(數論+幾何)、實際應用建模題(優化問題)、算法思維題(簡單編程邏輯)。
? 建立問題拆解框架:面對復雜問題時,采用"條件梳理→知識定位→模型構建→分步解決"的標準化流程。
? 訓練直覺猜想能力:通過特殊值檢驗、圖形直觀感知等方法快速探索解題方向。
四、 心理調整與臨場發揮保障
最后階段的準備需注重心理建設和考試當天的應對策略。
1. 壓力適應訓練
? 進行抗干擾模擬:在略有干擾的環境中進行模考,提升專注度。
? 建立積極心理暗示:制定分數目標區間(如100-115分),避免完美主義焦慮。
? 呼吸放松法練習:在遇到難題時進行30秒深呼吸調整,避免緊張情緒蔓延。
2. 臨場應對方案
? 物資準備清單:提前準備準考證、身份證件、多個計算器、鉛筆、手表等。
? 突發情況預案:如遇設備故障、臨時不適等問題時的應對流程。
? 后程時間管理:最后15分鐘必須預留5分鐘檢查時間,重點核對前15題的基礎題答案。
? 交卷前最終檢查:確認答題卡填涂無誤、沒有漏題,核對關鍵計算步驟。
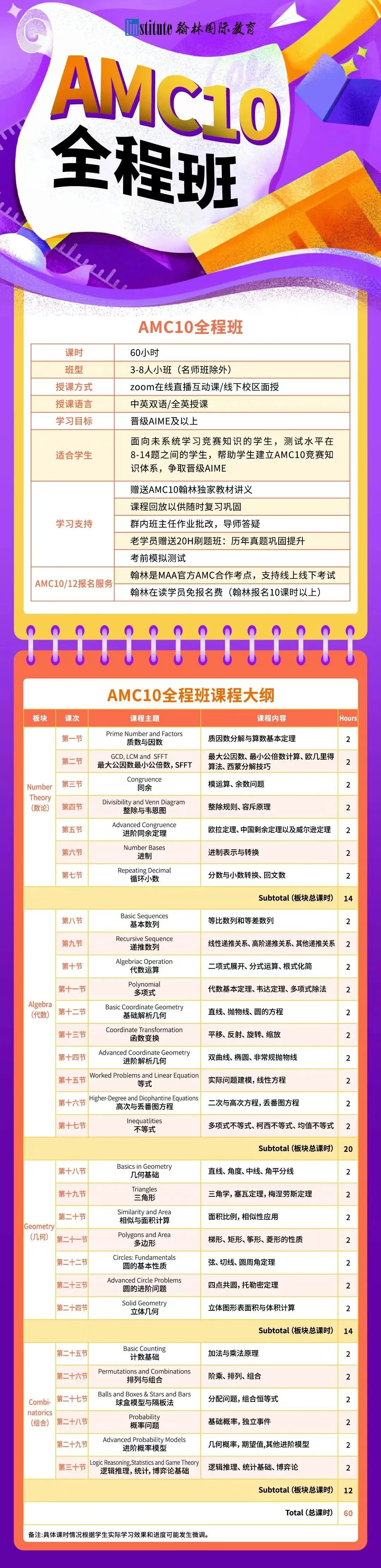
翰林AMC10培訓班
翰林AMC10培訓班