翰林國際教育，國內國際競賽領域的開拓者與引領者。我們不僅是系統輔導與深度教研的先行者，更為整個行業提供權威的賽事資訊與海量真題講義。在數學、物理、化學、生物、計算機、商科、數模等核心領域，我們的戰績長期穩居頭部領先地位，屢屢斬獲國家隊級別最高榮譽。作為同時擁有學科培訓、AP國際學校及美高資質的權威教育組織，我們為學生提供一站式的卓越培養體系，助力英才邁向世界頂尖學府。

AMC10競賽知識點系統匯總

AMC10的知識體系可劃分為四大核心模塊：代數、幾何、數論、組合。每個模塊都包含了從基礎到進階的豐富內容。

1. 代數（Algebra）

- 側重于函數、方程與技巧

● ?代數是AMC10中占比最重、應用最廣泛的模塊，強調抽象思維和靈活變形。 多項式與方程 ? 多項式運算： 多項式的加、減、乘、除，特別是多項式除法與長除法技巧。

○ ? 余數定理與因式定理： 多項式f(x)除以(x - a)的余數為f(a)。若f(a)=0，則(x - a)是f(x)的一個因式。這是求解高次方程根的關鍵。

○ ? 韋達定理及其推廣： 對于二次方程ax2+bx+c=0，根與系數有關系：x?+x? = -b/a, x?x? = c/a。對于更高次方程，也存在對稱多項式形式的根與系數關系。

○ ? 特殊高次方程： 可因式分解的高次方程、可通過換元法轉化為二次方程的方程（如雙二次方程）、以及一些特殊形式的方程。

● ? 不等式 ? 均值不等式（AM-GM）： 若干個非負數的算術平均數不小于其幾何平均數，這是證明和求解最值問題的最強大工具之一。

○ ? 柯西-施瓦茨不等式、排序不等式等： 這些是不等式領域的進階工具，常用于處理更復雜的最值問題。

○ ? 不等式求解： 涉及二次不等式、分式不等式及絕對值不等式。

● ? 函數 ? 函數概念： 函數的定義、定義域和值域的確定（尤其注意分母、根號等限制條件）。

○ ? 具體函數類型： ? 二次函數： 頂點式、交點式、標準式之間的轉換，圖像性質（開口、對稱軸、頂點、截距），最值問題。

■ ? 指數與對數函數： 運算法則，圖像與性質，求解指數/對數方程。

■ ? 簡單三角函數： 正弦、余弦、正切在直角三角形中的定義，特殊角函數值，正弦定理和余弦定理（雖屬幾何，但常與代數結合）。

● ? 數列 ? 等差數列與等比數列： 通項公式，求和公式及其推導。

○ ? 遞推數列： 通過遞推關系定義數列，并求解其通項公式（如特征根法）。

○ ? 求和技巧： 裂項相消、錯位相減法等。

● ? 代數技巧進階 代數式恒等變形、配方、對稱多項式、構造法、設而不求等高級解題策略。

2. 幾何（Geometry）

- 側重于圖形性質與空間想象

● ?幾何模塊要求考生具備敏銳的觀察力和嚴謹的邏輯推理能力。 平面幾何進階 ? 三角形： ? 重要定理： 正弦定理、余弦定理、角平分線定理、塞瓦定理、梅涅勞斯定理。

■ ? 心： 內心、外心、垂心、重心（統稱“四心”）的性質及其坐標表示。

■ ? 特殊三角形： 等邊、等腰、直角三角形的性質與判定。

○ ? 圓： ? 圓冪定理： 相交弦定理、切割線定理、割線定理的統一表述。

■ ? 圓與四邊形： 圓內接四邊形的判定與性質（對角互補、外角等于內對角），圓外切四邊形的性質（對邊之和相等）。

■ ? 四點共圓： 多種判定方法（如對角互補、同底同側等角）。

○ ? 多邊形： 正多邊形的角度、邊長、面積、外接圓與內切圓的關系。

○ ? 解析幾何入門： 坐標系中點的距離、中點公式、直線方程（點斜式、兩點式）、圓方程、直線與圓的位置關系。

● ? 立體幾何 ? 空間關系： 點、線、面的平行與垂直關系。

○ ? 三維坐標系： 空間點的坐標、距離公式。

○ ? 常見幾何體： ? 多面體： 棱柱、棱錐（特別是正棱錐）的體積與表面積計算。

■ ? 旋轉體： 圓柱、圓錐、球的體積與表面積公式。

○ ? 歐拉公式： 對于凸多面體，頂點數(V) - 棱數(E) + 面數(F) = 2。

3. 數論（Number Theory）

- 側重于整數的精妙性質

● ?數論是AMC10的特色和難點，考察思維的嚴謹性與創造性。 整數性質 ? 整除性： 整除規則（如被2, 3, 4, 5, 8, 9, 11等數整除的判定），帶余除法。

○ ? 質數與合數： 質數判定、質數分布、分解質因數。

○ ? 因數與倍數： 最大公約數(GCD)、最小公倍數(LCM)的求法（輾轉相除法）及應用。

○ ? 奇偶性分析： 利用奇偶性進行邏輯推理和排除選項。

● ? 模運算 ? 同余概念與基本性質： a ≡ b (mod m) 的含義，同余式的加、減、乘運算。

○ ? 復雜同余問題： 求大數的余數、利用同余解決整數分類問題、費馬小定理的初步應用。

● ? 進制 不同進制（如二進制、五進制、十六進制）與十進制之間的相互轉換，以及在特定進制下的運算。

● ? 丟番圖方程 主要是一次和二次不定方程，特別是勾股數組、佩爾方程等特殊形式的求解。

4. 組合（Combinatorics）

- 側重于計數與策略

● ?組合數學是衡量數學思維靈活性的重要標尺。 計數原理 ? 加法原理與乘法原理： 所有計數問題的基礎，必須準確理解“分類”與“分步”的區別。

○ ? 排列與組合： 區分是否與順序有關，熟練掌握P(n, r)和C(n, r)公式及適用場景。

○ ? 容斥原理： 解決重疊計數問題，公式：|A∪B| = |A| + |B| - |A∩B|，并可推廣至三個及以上集合。

● ? 二項式定理 公式：(a+b)^n = Σ [C(n, k) * a^(n-k) * b^k]。熟悉其通項公式及系數性質（如對稱性、各項系數和）。

● ? 概率 ? 古典概型： 概率 P = 滿足條件的情況數 / 所有可能的情況數。

○ ? 幾何概型： 利用長度、面積或體積的比例來計算概率。

○ ? 期望值： 離散隨機變量的期望值計算，即每個結果的值乘以其概率再求和。

● ? 組合方法進階 ? 遞推： 建立計數問題的遞推關系式（如斐波那契數列）并求解。

○ ? 對應原理： 通過建立一一映射將復雜計數問題轉化為簡單問題（如“隔板法”解決不定方程非負整數解問題）。

○ ? 分類討論： 對復雜問題根據特定標準進行不重不漏的分類。

○ ? 圖論與游戲問題： 簡單的圖論概念（如點、邊、路徑）、對策問題等。

AMC10高頻知識點考察分析

在四大模塊中，考察頻率和比重并非均等。根據歷年真題統計，其分布呈現出顯著規律：

● ? 代數與幾何占據絕對主導（合計超60%）： 這兩部分是數學的基礎支柱，是考查學生數學核心能力的主要陣地。代數更偏重計算與變形，幾何更偏重推理與洞察。

● ? 數論比重穩步提升： 因其能很好區分頂尖學生，數論題目的數量和難度近年來有所增加，成為高分的關鍵突破口。

● ? 組合是最大變數： 組合題目靈活多變，是主要難點和區分點。掌握基本原理后，更需要臨場的創造性思維。

各模塊內最常出現的具體考點包括：

● ? 代數模塊： ? 基礎運算與應用題： 比例、百分比、行程問題、工作效率問題等，難點在于準確理解題意并建立數學模型。

○ ? 多項式： 利用余數定理/因式定理求根或參數。

○ ? 數列： 等差數列與等比數列的求和問題，以及簡單的遞推數列。

● ? 幾何模塊： ? 三角形計算： 綜合運用勾股定理、相似、正弦/余弦定理求邊長或面積。

○ ? 圓的性質： 利用圓冪定理和四點共圓解決線段長度問題。

○ ? 面積計算： 圖形的割補法、等積變形。

● ? 數論模塊： ? 質因數分解： 求一個數的約數個數、約數和，或解決與乘積、整除相關的問題。

○ ? 模運算： 求大數除以某數的余數，或利用奇偶性、模分析解決整數存在性問題。

● ? 組合模塊： ? 基本計數： 熟練運用排列組合、乘法原理解決受限的計數問題（如“不相鄰”用插空法）。

○ ? 概率計算： 古典概型是絕對主流，關鍵是準確計數。

AMC10高頻易錯點深度解析

許多學生知識點已掌握，卻在考試中失分，根源往往在于以下易錯點：

1. 代數（Algebra）易錯點

● ? 應用題審題不清： 未能捕捉關鍵信息（如“至少”、“至多”、“翻倍”、“提前”），或忽略單位換算（小時/分鐘、米/厘米）。

● ? 絕對值與根式處理不當： 求解含絕對值方程或不等式時，忽略正負討論；處理根式時忽略定義域（被開方數非負）。

● ? 指數/對數運算性質混淆： 尤其是log(a+b) ≠ log a + log b這類錯誤。

● ? 韋達定理應用錯誤： 在使用x?2 + x?2 = (x?+x?)2 - 2x?x?等變形時，忘記系數a的影響。

2. 幾何（Geometry）易錯點

● ? “想當然”的幾何直觀： 僅憑圖形外觀作出判斷，忽視嚴格證明。例如，看似垂直的角未必是90度，看似相等的線段未必相等。

● ? 全等/相似三角形判定錯誤： 未能準確找到對應角或對應邊，尤其是在復雜圖形中。

● ? 漏解或多解： 幾何問題經常存在多種情況（如高在三角形內部或外部、圓與圓的位置關系），考生因思維定式而漏解。

● ? 解析幾何計算失誤： 距離公式、中點公式等計算繁瑣，容易在正負號上出錯。

3. 計數（Counting）易錯點

● ? 排列與組合混淆： 無法判斷問題是否與順序有關。例如，“選派代表”是組合，“排成一排”是排列。

● ? 重復計數： 這是組合計數中最常見的錯誤。在使用乘法原理或分類討論時，方案之間并非完全獨立，導致某些情況被多次計算。

● ? 遺漏計數： 與重復計數相反，分類標準不清晰，導致某些合法情況被忽略。

● ? 隔板法應用條件不清： 隔板法（Sticks and Bars）要求分配對象是 相同的 ，且用于解決“每份至少一個”的問題。若條件變化（如允許為0），需進行轉化。

4. 數論（Number Theory）易錯點

● ? 質數概念模糊： 誤認為1是質數，或忘記2是唯一的偶質數。

● ? 模運算性質錯誤： 錯誤地認為除法也滿足同余性（即a ≡ b (mod m) 不能直接推出a/c ≡ b/c (mod m)）。

● ? 枚舉不完整： 在解決整數解問題時，枚舉所有可能情況時發生遺漏。

5. 概率（Probability）易錯點

● ? 基本事件空間定義錯誤： 未能確保所有基本事件是等可能的。

● ? 條件概率理解偏差： 混淆P(A|B)和P(B|A)。

● ? 幾何概型度量錯誤： 在計算幾何概率時，對長度、面積或體積的度量計算錯誤。

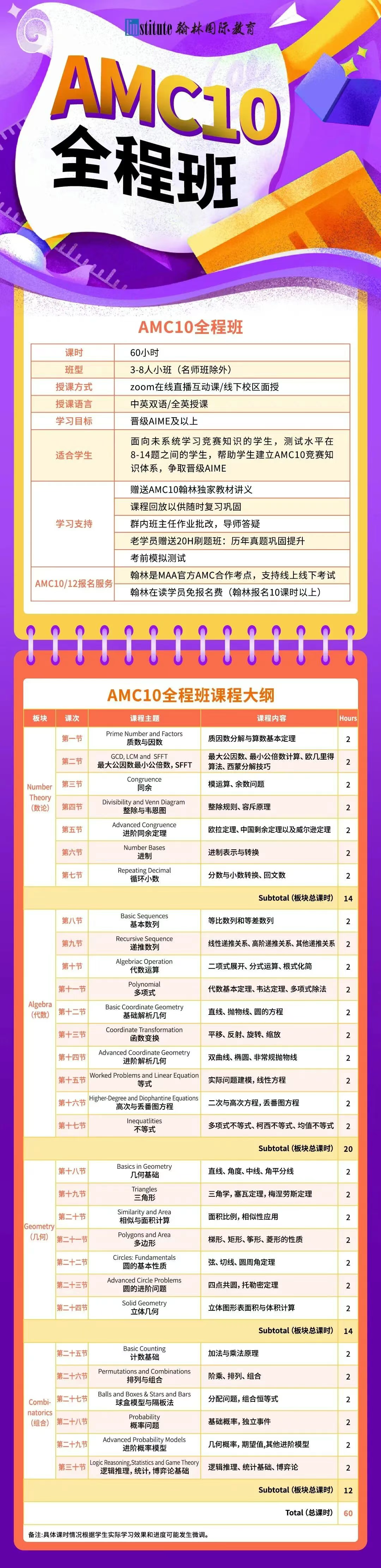
翰林AMC10培訓班

翰林AMC10培訓班