AMC10數學競賽核心知識點

AMC10（American Mathematics Competition 10）面向10年級及以下學生（通常為高一/初三學生），是沖刺AIME（美國數學邀請賽）的關鍵賽事，題目難度高于校內數學，注重邏輯推理與綜合應用。其核心知識點聚焦以下6類：

1. ? ?代數綜合與函數進階 ：

核心考點包括二次函數（頂點式/交點式應用）、多項式運算（因式分解/余數定理）、分式方程與不等式（含絕對值不等式）、數列（等差/等比數列求和、遞推關系）、函數圖像分析（單調性/對稱性）。AMC10代數題占比約35%-40%，需熟練掌握公式變形與實際問題建模（如利潤/距離最值）。

2. ? ?幾何深度與定理拓展 ：

覆蓋三角形全等/相似（擴展至梅涅勞斯/塞瓦定理基礎）、圓的性質（圓周角定理/切線長定理）、四點共圓判定、立體幾何（棱柱/圓錐體積與表面積）、解析幾何基礎（直線斜率/距離公式）。幾何題占比約25%，常需構造輔助線或運用定理鏈解決復雜問題（如角度計算/面積分割）。

3. ? ?數論進階與整除規律 ：

相比AMC8，AMC10數論更深入，包括質數分布（如埃拉托斯特尼篩法應用）、最大公約數/最小公倍數的綜合計算、同余定理（線性同余方程基礎）、完全平方數/立方數特征、進制轉換（如二進制/十進制互算）。數論題占比約10%-15%，常結合代數或邏輯推理出題。

4. ? ?組合數學與計數原理 ：

重點考察排列組合（含重復元素排列、分組問題）、概率計算（條件概率/獨立事件）、邏輯推理（如比賽排名/抽屜原理）、二項式定理基礎。組合題占比約15%，需掌握分類討論與避免重復計數（如容斥原理初步）。

5. ? ?統計與數據分析 ：

要求讀懂統計圖表（直方圖/散點圖/箱線圖）、計算平均值/中位數/眾數，分析數據分布特征（如離散程度），并解決簡單實際問題（如根據數據預測趨勢）。統計題占比約5%-10%，側重信息轉化能力。

6. ? ?代數與幾何綜合應用 ：

AMC10壓軸題常融合代數與幾何知識（如用函數解析式求圖形交點、通過幾何條件建立方程），需靈活切換思維模式，綜合運用多個知識點解題。

AMC12數學競賽核心知識點

AMC12（American Mathematics Competition 12）面向12年級及以下學生（通常為高三/高二學生），是沖刺AIME和名校申請的重要賽事，難度顯著高于AMC10，覆蓋部分大學初級數學內容。其核心知識點聚焦以下6類：

1. ? ?高等代數與函數拓展 ：

包含多項式高階運算（復數根/韋達定理擴展）、對數與指數函數（復合函數性質）、三角函數（和差化積/倍角公式、圖像變換）、極限基礎（數列極限概念）、復數運算（模/共軛復數）。AMC12代數題占比約30%-35%，需掌握大學預科級公式應用（如歐拉公式基礎）。

2. ? ?幾何高階與定理深化 ：

覆蓋圓冪定理（切割線定理/相交弦定理）、托勒密定理、海倫公式（三角形面積）、立體幾何綜合（球體/棱錐體積計算）、解析幾何（圓的方程/拋物線基礎）。幾何題占比約20%-25%，常需構造輔助線或運用高階定理鏈（如反演變換基礎）。

3. ? ?數論深度與競賽級應用 ：

包括二次剩余（基礎概念）、費馬小定理/歐拉定理（數論證明題）、連分數基礎、高階同余方程（中國剩余定理擴展）、質因數分解綜合應用。數論題占比約15%，是AMC12區分高分段的關鍵模塊。

4. ? ?組合數學與概率深化 ：

重點考察排列組合高階（含限制條件排列、容斥原理應用）、概率分布（幾何概率/條件概率鏈）、復雜邏輯推理（如無限步驟問題）、設計組合（如覆蓋問題）。組合題占比約15%-20%，需靈活運用數學歸納法與分類討論。

5. ? ?微積分預備知識 ：

AMC12允許使用微積分思維（不超綱），涉及導數概念（變化率/極值初步）、積分基礎（面積近似計算）、數列極限（收斂性判斷）。微積分相關題占比約5%，常作為壓軸題的解題工具。

6. ? ?跨模塊綜合與創新題 ：

AMC12壓軸題（如第21-25題）常融合代數、幾何、數論與組合知識（如用函數性質解幾何最值、通過數論條件構造組合模型），需構建多維度解題思路，考驗數學直覺與創造力。

AMC10數學競賽賽制設置

1. ? ?參賽資格與分組 ：

面向全球10年級及以下學生（考試當天年齡不超過17.5周歲），無國籍/地域限制，數學基礎扎實的初中生/高中低年級學生均可報名。

2. ? ?考試時間與頻次 ：

每年僅1場（通常在11月舉行，分A/B兩場考試，間隔1周），考生任選一場或兩場參賽（取最高分晉級）。

3. ? ?試卷結構與題型 ：

滿分150分，共25道單項選擇題（每題6個選項），答對得6分，答錯得0分，不答得1.5分（鼓勵謹慎作答）。

4. ? ?難度梯度設計 ：

前10題為基礎題（校內數學延伸），11-20題為中等題（需邏輯推理），21-25題為壓軸題（綜合應用+高階思維），整體難度高于AMC8，接近高中數學聯賽入門水平。

5. ? ?晉級與獎項規則 ：

全球成績前2.5%左右（約100-110分）可晉級AIME美國數學邀請賽；獎項分全球卓越獎（滿分）、全球優秀獎（全球前5%）、AIME晉級資格獎及學校/年級榮譽獎。

6. ? ?考試形式與支持 ：

國內多為線上機考（需配備攝像頭監考），部分城市設線下考點；提供中英雙語試卷（選項為英文），允許使用無存儲功能的計算器（具體以當年要求為準）。

AMC12數學競賽賽制設置

1. ? ?參賽資格與定位 ：

面向全球12年級及以下學生（考試當天年齡不超過19.5周歲），適合高中各年級數學能力突出者，是沖擊頂尖大學數學背景的重要賽事。

2. ? ?考試時間與場次 ：

與AMC10同步（每年11月舉行，分A/B兩場考試），考生可單獨報AMC12或同時參加AMC10/12（取最佳成績晉級）。

3. ? ?試卷結構與評分 ：

滿分150分，25道單項選擇題（每題6選1），答對得6分，答錯得0分，不答得1.5分（策略與AMC10一致）。

4. ? ?難度與知識范圍 ：

覆蓋全部高中數學內容（包括三角函數、復數、進階代數、立體幾何、概率統計等），前15題與AMC10難度接近，16-25題深度顯著提升（需大學預科數學思維，如微積分初步思想、數論高階定理）。

5. ? ?晉級與榮譽體系 ：

全球前5%左右（約85-95分）可晉級AIME；獎項包括全球卓越獎（滿分）、全球優秀獎（全球前5%）、AIME晉級資格獎，高分選手受藤校/Top30院校高度關注。

6. ? ?考試支持與策略 ：

同樣提供中英雙語試卷，允許使用無存儲功能計算器；備考需系統學習高中競賽數學（如AMC12專屬知識點：多項式定理、數論中的費馬小定理應用、組合中的高級計數方法），建議搭配AIME真題訓練提升綜合能力。

兩賽事均以“選拔數學尖子生”為核心，AMC10側重高中數學基礎延伸，AMC12更挑戰高階知識應用，是沖擊AIME及頂尖大學的黃金跳板！

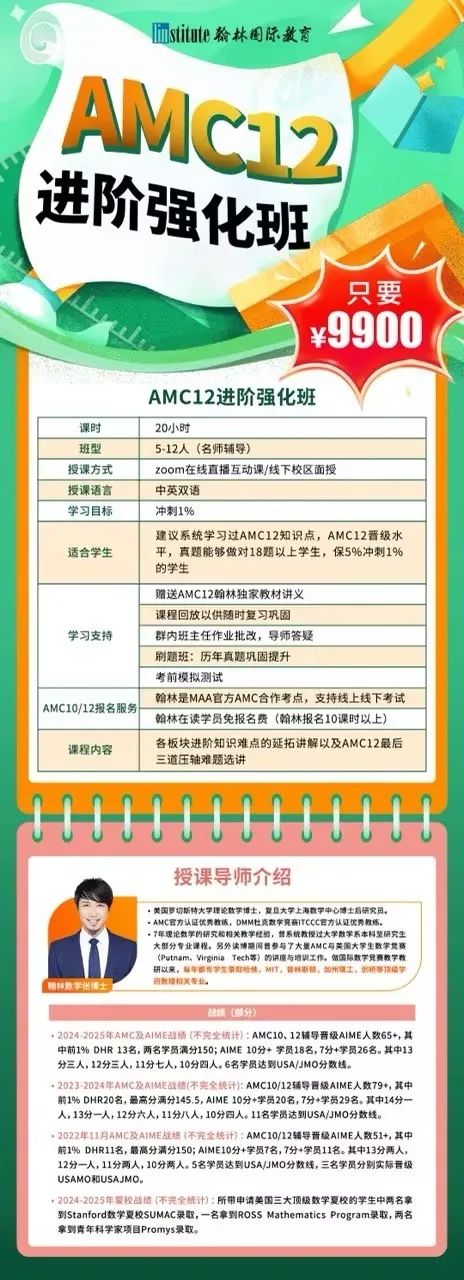
翰林AMC12培訓班

想沖刺AMC12全球1%嗎？翰林國際教育AMC12進階強化班來助力！20小時名師精講，中英雙語授課，5 - 12人小班輔導。贈送獨家教材，還有真題答疑等服務。系統鞏固知識，突破壓軸難題。僅需9900元，開啟你的競賽進階之旅！

翰林AMC12培訓班

添加微信小助手在線咨詢