- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
USACO 2018 December Contest Silver 3 MOOYO MOOYO
With plenty of free time on their hands (or rather, hooves), the cows on Farmer John's farm often pass the time by playing video games. One of their favorites is based on a popular human video game called Puyo Puyo; the cow version is of course called Mooyo Mooyo.
The game of Mooyo Mooyo is played on a tall narrow grid cells tall ( ) and 10 cells wide. Here is an example with :
0000000000 0000000300 0054000300 1054502230 2211122220 1111111223
Each cell is either empty (indicated by a 0), or a haybale in one of nine different colors (indicated by characters 1..9). Gravity causes haybales to fall downward, so there is never a 0 cell below a haybale.
Two cells belong to the same connected region if they are directly adjacent either horizontally or vertically, and they have the same nonzero color. Any time a connected region exists with at least cells, its haybales all disappear, turning into zeros. If multiple such connected regions exist at the same time, they all disappear simultaneously. Afterwards, gravity might cause haybales to fall downward to fill some of the resulting cells that became zeros. In the resulting configuration, there may again be connected regions of size at least cells. If so, they also disappear (simultaneously, if there are multiple such regions), then gravity pulls the remaining cells downward, and the process repeats until no connected regions of size at least exist.
Given the state of a Mooyo Mooyo board, please output a final picture of the board after these operations have occurred.
INPUT FORMAT (file mooyomooyo.in):
The first line of input contains and ( ). The remaining lines specify the initial state of the board.
OUTPUT FORMAT (file mooyomooyo.out):
Please output lines, describing a picture of the final board state.
SAMPLE INPUT:
6? 3
0000000000
0000000300
0054000300
1054502230
2211122220
1111111223
SAMPLE OUTPUT:
0000000000 0000000000 0000000000 0000000000 1054000000 2254500000
In the example above, if , then there is a connected region of size at least with color 1 and also one with color 2. Once these are simultaneously removed, the board temporarily looks like this:
0000000000 0000000300 0054000300 1054500030
2200000000 0000000003
Then, gravity takes effect and the haybales drop to this configuration:
0000000000 0000000000 0000000000 0000000000 1054000300 2254500333
Again, there is a region of size at least (with color 3). Removing it yields the final board configuration:
0000000000 0000000000 0000000000 0000000000 1054000000 2254500000
Problem credits: Brian Dean
USACO 2018 December Contest Silver 3 MOOYO MOOYO題解(翰林國際教育提供,僅供參考)
通過搜索(BFS或DFS)找到連通的區域,然后消去,然后模擬下落。
基本就是 mayan游戲 難度
實現細節:
1. 一般來說DFS比BFS好寫,如果可以選的話,建議DFS。
2. 計數和染色部分分開寫,如果寫在一起,非常麻煩。
3. 下落的部分,有不需要額外數組的寫法,建議學習。
#include <bits/stdc++.h>
using namespace std;
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
int n, k;
char s[120][12];
bool v[120][12];
bool in(int x, int y) {
return 0 <= x && x < n && 0 <= y && y < 10;
}
int dfs(int x, int y, char c) {
v[x][y] = true;
int re = 1;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (in(nx, ny) && s[nx][ny] == c && !v[nx][ny]) {
re += dfs(nx, ny, c);
}
}
return re;
}
void color(int x, int y, char c) {
s[x][y] = '0';
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (in(nx, ny) && s[nx][ny] == c) {
color(nx, ny, c);
}
}
}
bool gao() {
bool flag = false;
memset(v, 0, sizeof v);
for (int i = 0; i < n; i++) {
for (int j = 0; j < 10; j++) {
if (!v[i][j] && s[i][j] != '0') {
int sz = dfs(i, j, s[i][j]);
if (sz >= k) {
flag = true;
color(i, j, s[i][j]);
}
}
}
}
return flag;
}
void fall() {
for (int j = 0; j < 10; j++) {
int c = 0;
for (int i = 0; i < n; i++) {
if (s[i][j] != '0') {
s[c++][j] = s[i][j];
}
}
while (c < n) {
s[c++][j] = '0';
}
}
}
int main() {
freopen("mooyomooyo.in", "r", stdin);
freopen("mooyomooyo.out", "w", stdout);
scanf("%d%d", &n, &k);
for (int i = n - 1; i >= 0; i--) {
scanf("%s", s[i]);
}
while (gao()) {
fall();
}
for (int i = n - 1; i >= 0; i--) {
printf("%sn", s[i]);
}
return 0;
}[/hide]
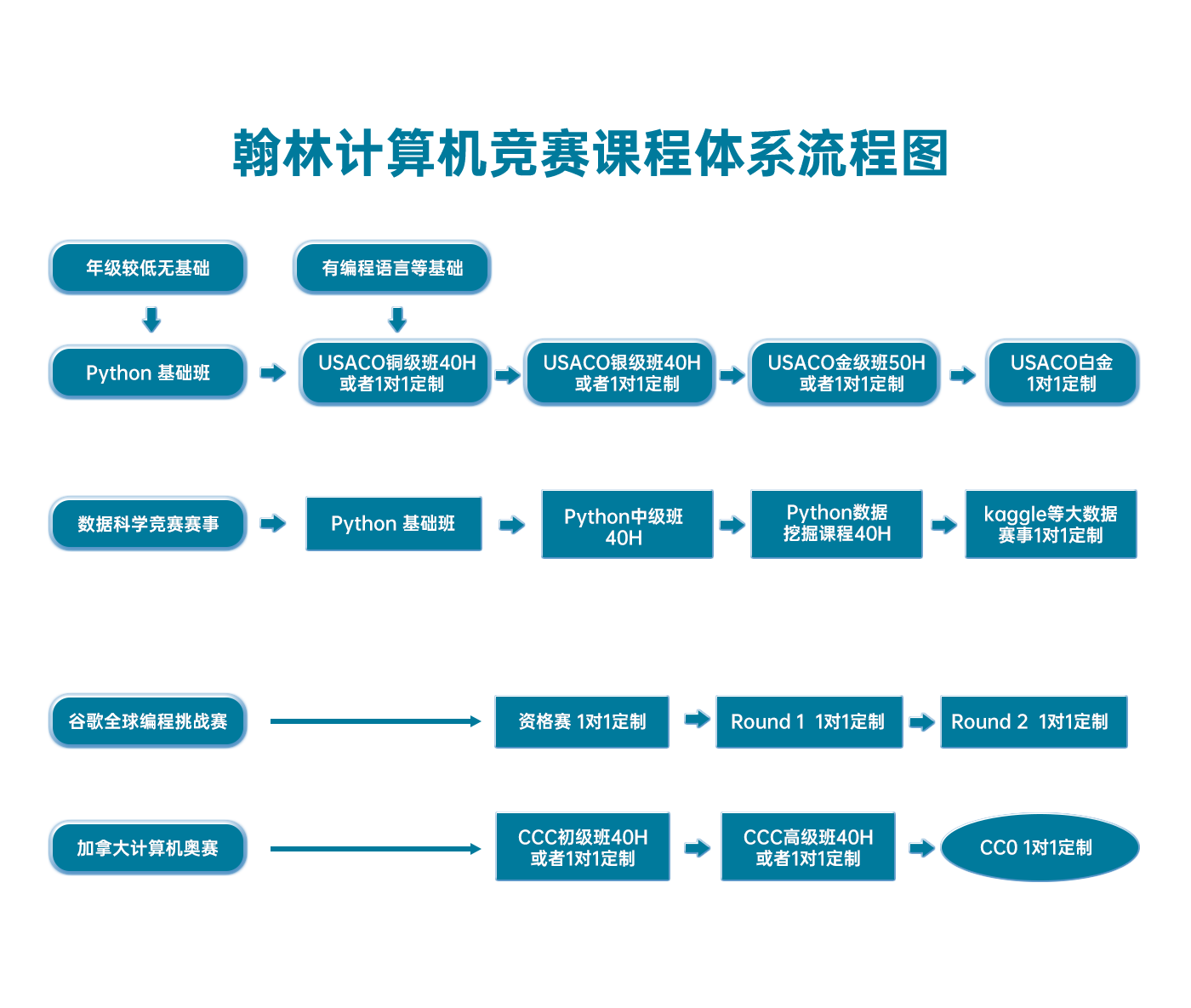
翰林USACO課程體系流程圖

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









