- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
USACO十一算法camp小結-Day1
Day1?總結
單獨約談各位學員,了解大家的基礎,編程語言學習歷史,和比USACO的計劃
根據(jù)各位同學的語言基礎調整課程形式,降低課程難度
快速了解OI賽事的特點
練習2018USACO2月銅題1-3題(首次中文題),熟悉USACO賽事的難度,比賽形式
答題通過情況(AC)
銅1?全員通過
銅2?黃常麟 韓子鍵 余鐵琳 陳晟勱 石博聞 徐常捷
銅3?余鐵琳?孔伯銘?石博聞?Daniel
銀1?石博聞?Daniel?孔伯銘(部分)
銀2?石博聞
6.下午講解算法:倍增,排序,貪心,歐幾里德算法等 算法詳細內(nèi)容及參考資料總結:
7. 晚餐全體人員聚餐
8.聚餐后部分學員繼續(xù)攻克代碼,直到現(xiàn)在(晚上10:00pm)
畢克導師課程講稿(含大量參考鏈接內(nèi)容,信息量大,建議收藏)
1自我介紹
畢克
2010 ~ 2013,?家莊?中。
NOI 2012 ?牌。
2013 ~ 2017,清華?學。
5 次區(qū)域賽/EC-FINAL ?牌。
沒去過 IOI,也沒去過 ACM World Final。現(xiàn)在在?港上學(劃?)。
三?愛好:?賽,出題,講課。
QQ:751723392,?Email:wwwwodddd@gmail.com
2Competitive programming
算法?賽?是?種?較成熟的?賽形式。
簡單來說,就是按照題?要求,讀取指定格式的輸?,經(jīng)過?些處理,按照指定格式輸出。最簡單的輸出?較就是逐字節(jié)?較,也就是輸出必須和答案?模?樣,才算正確;當然也有
的題?是 Special Judge,也就是只要滿??定條件即可。
?般情況下,除了反作弊的需要之外,不關注代碼如何實現(xiàn)的。
?常客觀。?便??調試。
增加?個參賽選?,額外代價很低。
對于?中階段
中國的?賽有 NOIP 和 NOI。美國的?賽有 USACO。
2.1???? 學習的意義
?中階段學習 OI,可以保送?學。
?學階段學習 ACM,可以獲得部分公司的青睞。(然后也可以?賽,出題,講課,?上經(jīng)濟獨?之路。)
3評測結果
3.1AC (Accepted)
表?通過。
3.2WA (Wrong Answer)
表?程序成功運?,但是輸出和標準答案不?樣,或者是沒有通過 Special Judge 的檢測。
3.3 CE (Compile Error)
編譯失敗,需要注意在線的編譯器和你使?的編譯器不?定?樣,有?常多的原因會導致本機可以編輯,提交得到 CE。
3.4RE (Runtime Error)
表?程序崩潰。
有三種可能,數(shù)組越界,爆棧,除以 0。
3.5 TLE (Time Limit Exceeded)
程序使?的時間過長,沒有順利運?完成。
有兩種可能,算法太慢,或者是出現(xiàn)了死循環(huán)。
3.6MLE (Memory Limit Exceeded)
程序使?的空間過?,沒有順利運?完成。
3.7OLE (Output Limit Exceeded)
程序不停的輸出,于是被結束了。
4 常見錯誤
4.1不要輸出任何多余字符
不要輸出任何多余字符,提?語句,或者是調試語句。
?如不要輸出 please input an integer: 或者 the answer is。
4.2程序要順利結束
在上古時期寫程序,如果什么都不加,程序編譯運?后會?閃?過。所以常常在結尾加上 system("pause") 或者 while(1);
4.3看清題目數(shù)據(jù)范圍
除了剛開始學編程,絕?多數(shù)題?都需要?定優(yōu)化,?定要考慮在最壞的情況下程序能否運?。
復雜度 (Complexity)
5.1時間復雜度
我們特別關注運?時間與輸?規(guī)模的關系。
對于運?時間,我們?般考慮基本操作的次數(shù)。
?如可以認為?次運算是基本操作,?次賦值或者?較也是基本操作。
特別的,?般情況下并不關?常數(shù)問題,?如 a += b 可以看做?次基本操作,也可以看做兩次基本操作。
這就是?家常常說的 O(n),O(n2) 的意思。
5.2????? 空間復雜度
對于算法?賽來說,不需要特別關注這個內(nèi)容。
?個 int 是 4 字節(jié),106 個 int 是 4MB,其他的空間??以此類推。需要注意的是,即使什么都不寫,也會占??百 KB 的空間。
USACO?比賽介紹
12 ?,1 ?,2 ?,和?場 US Open。
每次分為四個級別:Bronze, Silver, Gold, Platinum。
每次在 72 ?時中選擇 4 ?時參加(不要問我如何防?作弊) 剛開始只能參加 Bronze,達到?定分數(shù)之后可以參加下?級。
?賽實時返回結果。
不要抄襲,?賽中不要進?代碼上的交流。
不能打表,你不能本機運算出所有輸?的答案,然后打表提交。(當然我覺得打表主要和出題?平有關)
7C++
學會查?檔。
中??檔
英??檔
另?份英??檔
7.1????? 變量
各個類型的變量是有范圍的,具體來說跟?進制有關。反碼
補碼
?家注意浮點數(shù) double 的存儲?式,類似科學計數(shù)法
IEEE 754
7.2運算符
注意運算優(yōu)先級,尤其是位運算部分。注意異或和 power。
注意短路運算?與位運算的區(qū)別。
注意單?運算符負號,與減法的區(qū)別注意運算中類型的強制轉換
7.3判斷和循環(huán)
沒什么好講的,相信?家已經(jīng)掌握了。
STL
我認為 C++ 中?較有?的東西:
next_permutation sort
set map
priority_queue
7.5 信息學
信息學不需要 C++ 中華麗的特性。信息學寫的代碼基本是?次性的。
C++ 可以提供底層和頂層的書寫?式。
? Pascal 便于書寫。
? Python 效率?。
與之類似的還有 Java 語?,不過效率稍低。
信息學不關??戶體驗,只需要輸出應該輸出的即可。時間復雜度是影響程序速度的重要指標。
8Java
Java 是?個完全?向對象的語?基本語法和 C++ ?常相似但是要注意以下的不同。
庫函數(shù)的區(qū)別?如排序,等函數(shù),Java 的?法和 C++ 完全不同。還有?些容器,?如 Map Set 等也很不相同。
另外 Java 中對于對象(結構體)都是傳引?,?不是傳值。這也是值得注意的?點。
9Python
9.1交互式
Python 的交互功能?常好?,推薦每個?都學習使?。
并且 Python ?持計算?精度,可以?來當進階版的計算器。
9.2 變量
變量不需要聲明,不需要明確類型。
9.3 運行速度
Python 的運?速度?常慢,并且不容易被估計。并不建議在需要優(yōu)化效率的情況下使?。
Python 2 和 Python 3
Linux 計算機?般默認安裝 Python 2,所以建議學習 Python 2。當然如果你已經(jīng)會了 Python 3,也不?換,了解 Python2 和 3 的差別即可。
10USACO 2017
?共有四場?賽。難度逐漸增加。
從 2018 February 開始,題?描述開始有了簡體中?版。
11USACO 2017 December Contest, Bronze, Problem 1. Blocked Billboard
11.1題目背景
Blocked Billboard
11.2題目大意
求矩形?積交
11.3 題目解法
求矩形?積交
12USACO 2017 December Contest, Bronze, Problem 2. The Bovine Shuffle
12.1題目背景
The Bovine Shuffle
12.2題目大意
數(shù)組的嵌套使?。
12.3題目解法
數(shù)組的嵌套使? s[a[a[a[i]]]]。
13USACO 2017 December Contest, Bronze, Problem 3. Milk Measurement
13.1題目背景
Milk Measurement
13.2題目大意
模擬,三個數(shù)字求最?值。
13.3題目解法
模擬,三個數(shù)字求最?值。
14USACO 2018 January Contest, Bronze, Problem 1. Blocked Billboard II
14.1題目背景
Blocked Billboard II
14.2題目大意
分類討論,矩形?積交。
14.3 題目解法
分類討論,矩形?積交。
15USACO 2018 January Contest, Bronze, Problem 2. Life- guards
15.1 題目背景
Lifeguards
15.2題目大意
枚舉,模擬。
15.3 題目解法
枚舉,模擬。
16 USACO 2018 January Contest, Bronze, Problem 3. Out of Place
16.1題目背景
Out of Place
16.2題目大意
?個有序的數(shù)列中,插?了?個數(shù)字。
問?少多少次交換,可以使得這個序列再次變得有序。初始的序列中可能有相同的數(shù)字。
16.3題目解法
排序之后,檢查有多少個數(shù)字發(fā)?了變化。如果沒有,答案是 0。
如果有 k 個,那么需要 k ? 1 次交換。
17USACO 2018 February Contest, Bronze, Problem 1. Teleportation
17.1題目背景
Teleportation
17.2題目大意
數(shù)軸上兩點之間的距離。
17.3 題目解法
數(shù)軸上兩點之間的距離。
18 USACO 2018 February Contest, Bronze, Problem 2. Hoofball
18.1題目背景
Hoofball
18.2????? 題目大意
英語題
”the cow farthest to the left among these” 是指最左邊的,?不是指距離左邊最遠的。
18.3 題目解法
對于?頭?來說,如果沒?給他球,那么 John 必須給他。
特別的,如果對于孤?的 2 頭?,他們互相傳,那么 John 也必須給其中?個?。
19 USACO 2018 February Contest, Bronze, Problem 3. Taming the Herd
19.1 題目背景
Taming the Herd
19.2????? 題目大意
題目解法
如果?天是 x(x > 0),那么前?天必須是 x ? 1。如果?天需要是不同的數(shù)值,那么?解。
第?天必須是 0。
在滿?以上條件的情況下,所有 ?1 都可以變?yōu)?0 或變?yōu)橹暗臄?shù)字加?。
20USACO 2018 US Open Contest, Bronze, Problem 1. Team Tic Tac Toe
20.1 題目背景
Team Tic Tac Toe
20.2 題目大意
閱讀理解題
20.3 題目解法
選出來的 2 個字母?序。
必須是存在??,兩個都有才可以。
21USACO 2018 US Open Contest, Bronze, Problem 2. Milking Order
21.1? 題目背景
Milking Order
21.2題目大意
題目解法
考慮如何判斷?解,如果可以判斷?解,枚舉 1 ?的位置,然后判斷是否有解即可。
22 USACO 2018 US Open Contest, Bronze, Problem 3. Family Tree
22.1 題目背景
Family Tree
22.2????? 題目大意
題目解法
模擬
倍增
?處最?的就是快速冪
快速冪可以處理所有滿?結合律的東西。
24 Luogu P1226
24.1? 題目背景
24.2? 題目大意
快速冪
24.3 題目解法
快速冪
見多識?的同學可能覺得這個題可以?歐拉定理搶救?下。并沒有必要。
排序 (sort)
3 個 O(n2) 排序。
3 個 O(n log n) 排序。
快速排序,最常?。
歸并排序,可以算逆序對。
堆排序,只需要 O(1) 的額外空間。
貪心算法 (Greedy algorithm)
有很多?常好的貪?題?。
但是因為需要的知識過于艱深,所以只好先挑?些簡單的。
27??????? Luogu P1007
27.1????? 題目背景
27.2????? 題目大意
題目解法
假設相遇之后不是同時調頭,?是互相穿過。
28??????? Luogu P1208
28.1????? 題目背景
P1208 [USACO1.3] 混合?奶 Mixing Milk
28.2????? 題目大意
題目解法
按價格排序,然后貪?。
29??????? Luogu P1223
29.1????? 題目背景
29.2????? 題目大意
題目解法
對于第 i 個?,如果他倒數(shù)第 j 個接?,那么對全局的貢獻是 jti。所以接?快的,應該先接?。
30??????? bzoj 2563
30.1????? 題目背景
30.2????? 題目大意
題目分析
貪?!
遞歸
遞歸本質上并不需要存在,只是為了程序容易實現(xiàn)。
?些例?:階乘,F(xiàn)ibonacci 數(shù)。遞推式,終?條件。
32??????? 歐幾里得算法
計算最?公約數(shù):歐??得算法
33??????? 搜索
枚舉所有的狀態(tài)。
33.1????? 枚舉所有子集
枚舉??為 n 的集合的所有?集。
?位運算。
枚舉?集的?集。
33.2????? 枚舉固定大小的子集
枚舉??為 n 的集合的所有??為 m 的?集。
next permutation
似乎有?種?位運算的?法,但是我記不得了。
33.3????? 枚舉所有排列
枚舉 1 到 n 的所有排列。深搜。
next permutation。
值得注意的是。next permutation 處理有重復元素的時候,不會把相同的排列?成 2 次。
33.4????? 其他
但是在很多情況下,還是需要?深搜的
34??????? 深度優(yōu)先搜索(搜索)
?棧。
但是因為有遞歸,這個棧,并不需要你來實現(xiàn)。
?般適?于:找到任意?個解,或者找到所有解。或者是狀態(tài)?常?,不適合深度優(yōu)先搜索。
34.1????? 細節(jié)
核?在于狀態(tài)更新與復原。
有的時候還需要標記 visited 數(shù)組,表?這個狀態(tài)被搜過了。
35??????? 剪枝
遇到?些不合法的狀態(tài),可以直接剪枝,?不是等到枚舉到最后再剪枝。
36??????? 廣度優(yōu)先搜索(搜索)
?隊列。
需要??實現(xiàn)隊列。
?般適?于:找到步數(shù)最?的解。 注意隨著步數(shù)增加,狀態(tài)指數(shù)增長。
36.1????? 細節(jié)
核?在于把狀態(tài)壓縮,要能存下。
有的時候還需要標記 visited 數(shù)組,表?這個狀態(tài)被搜過了。
37??????? 雙向廣度優(yōu)先搜索
從最開始的狀態(tài)和最后的狀態(tài)?起搜索。
這樣只需要最?步數(shù)的?半,就可以搜出答案了。
隨著步數(shù)增加,狀態(tài)指數(shù)增長,步數(shù)減少?半,狀態(tài)減少明顯!
38??????? IDA*
每個狀態(tài)很?,并不能?搜? 要求最?步數(shù)?
枚舉最?步數(shù),然后深搜判斷有沒有解。
每多?層,多花費的時間是上?層的數(shù)倍,上?層的時間可以忽略。
39??????? Luogu P1219
39.1????? 題目背景
39.2????? 題目大意
經(jīng)典問題?皇后。
39.3????? 題目解法
直接深搜即可。
40??????? Luogu P1312
40.1????? 題目背景
40.2????? 題目大意
NOIP 2011 的?個搜索模擬題。
40.3????? 題目解法
41??????? bzoj 1501
41.1????? 題目背景
41.2????? 題目大意
暴?搜索。
41.3????? 題目分析
需要努?寫代碼。
翰林USACO課程體系流程圖
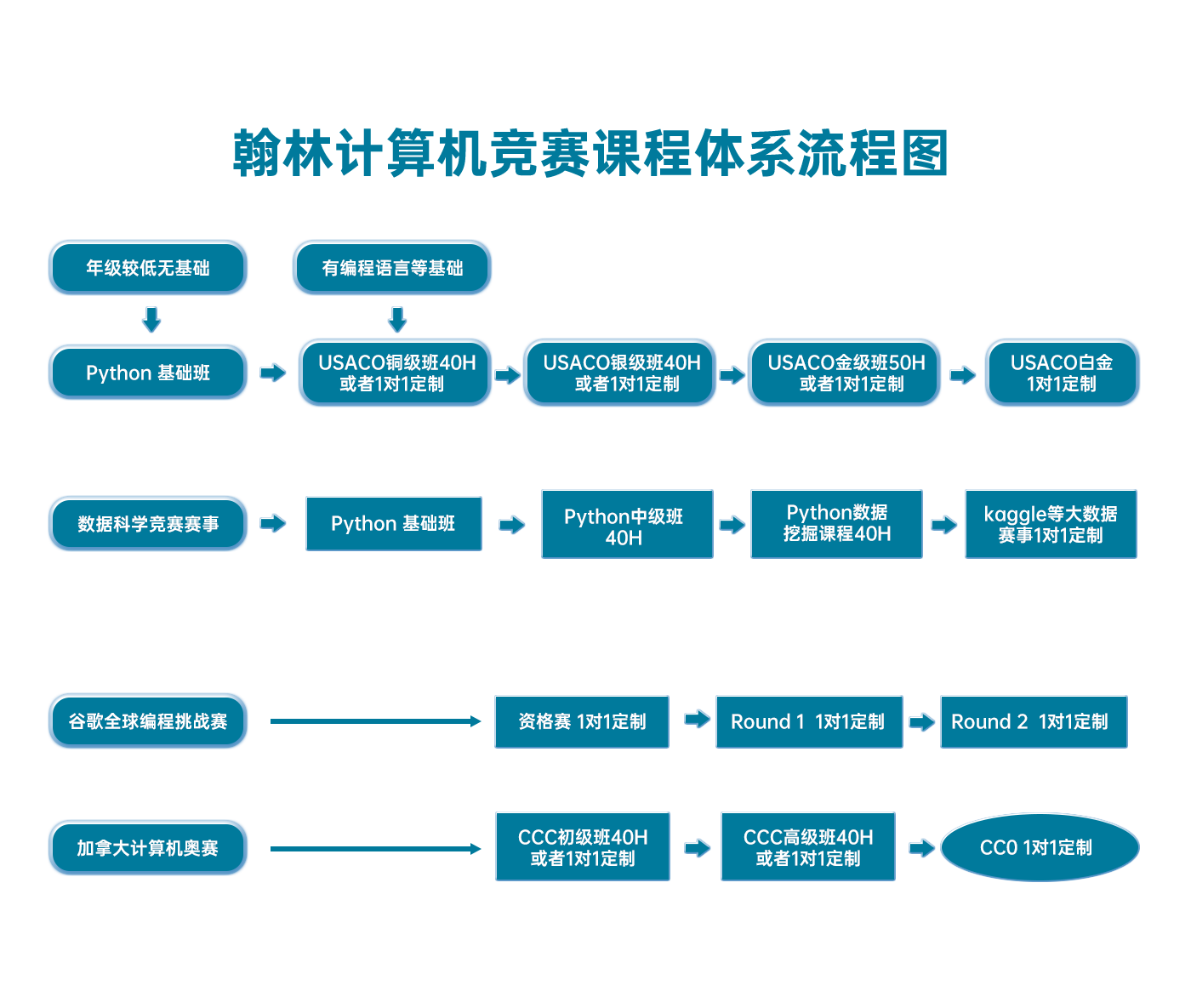

最新發(fā)布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









